Populär-wissenschaftliche Vorlesungen

Anzeige. Gutenberg Edition 16. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++

XII.
Über das Prinzip der Erhaltung der Energie.

Dieser Artikel, eine freie Bearbeitung eines Teiles meiner Schrift über »Erhaltung der Arbeit«, erschien zuerst englisch in »The Monist«. Vol. V. p. 22.

In einem durch seine liebenswürdige Einfachheit und Klarheit ausgezeichneten populären Vortrag, den Joule im Jahre 1847 gehalten hat, On Matter, Living Force, and Heat. Joule, Scientific Papers. London 1884. I. p. 265. setzt dieser berühmte Physiker auseinander, daß die lebendige Kraft, die ein schwerer Körper im Fall durch eine gewisse Höhe erlangt hat, welche derselbe in Form der beibehaltenen Geschwindigkeit mit sich führt, das Äquivalent der Attraktion durch den Fallraum ist, und daß es » absurd« wäre anzunehmen, jene lebendige Kraft könnte zerstört werden, ohne dieses Äquivalent wieder zu erstatten. Er fügt dann hinzu: You will therefore be surprised to hear that until very recently the universal opinion has been that living force could be absolutely and irrevocably destroyed at any one's option.« Nehmen wir hinzu, daß heute, nach 47 Jahren, das Gesetz der Erhaltung der Energie, so weit die Kultur reicht, als eine vollkommen ausgemachte Wahrheit gilt, und auf allen Gebieten der Naturwissenschaft die reichsten Anwendungen erfährt.

Das Schicksal aller bedeutenden Aufklärungen ist ein sehr ähnliches. Beim ersten Auftreten werden dieselben von der Mehrzahl der Menschen für Irrtümer gehalten. So wurde J. R. Mayers Arbeit über das Energieprinzip (1842) von dem ersten physikalischen Journal Deutschlands zurückgewiesen, Helmholtz' Abhandlung erging es (1847) nicht besser, und auch Joule scheint nach einer Andeutung von Playfair mit seiner ersten Publikation (1843) auf Schwierigkeiten gestoßen zu sein. Allmählich aber erkennt man, daß die neue Ansicht längst wohl vorbereitet und spruchreif war, nur daß wenige bevorzugte Geister das weit früher wahrgenommen hatten, als die andern, wodurch sich eben die Opposition der Majorität ergab. Mit dem Nachweis der Fruchtbarkeit der neuen Ansicht, mit ihrem Erfolg, wächst das Vertrauen zu derselben. Die Majorität der Menschen, welche die Ansicht verwendet, kann auf das gründliche Studium derselben nicht eingehen; sie nimmt den Erfolg für die Begründung. So kann es geschehen, daß eine Ansicht, welche die bedeutendsten Entdeckungen herbeigeführt hat, wie die Blacksche Wärmestofftheorie, zu einer spätern Zeit auf einem Gebiet, wo sie nicht zutrifft, ein Hemmnis des Fortschrittes wird, indem dieselbe die Menschen geradezu blind macht gegen Tatsachen, welche der beliebten Theorie nicht entsprechen. Soll eine Theorie vor dieser zweifelhaften Rolle bewahrt werden, so müssen von Zeit zu Zeit die Gründe und Motive ihrer Entwicklung und ihres Bestehens auf das Genaueste untersucht werden.

Durch mechanische Arbeit können die verschiedensten physikalischen (thermischen, elektrischen, chemischen u. s. w.) Veränderungen eingeleitet werden. Werden dieselben rückgängig, so erstatten sie die mechanische Arbeit wieder, genau in dem Betrage, welcher zur Erzeugung des rückgängig gewordenen Teiles nötig war. Darin besteht der Satz der Erhaltung der Energie. Für das unzerstörbare Etwas, als dessen Maß die mechanische Arbeit gilt, ist allmählich der Name Energie in Gebrauch gekommen. Derselbe scheint zuerst von Th. Young auf dem Gebiete der Mechanik eingeführt zu sein. Wie sind wir zu dieser Einsicht gelangt? Aus welchen Quellen haben wir dieselbe geschöpft? Diese Frage ist nicht nur an sich von dem höchsten Interesse, sondern auch aus dem oben berührten Grunde.

Die Meinungen über die Grundlagen des Energiegesetzes gehen heute noch sehr weit auseinander. Manche führen den Energiesatz auf die Unmöglichkeit eines perpetuum mobile zurück, welche sie entweder als durch die Erfahrung hinlänglich erwiesen oder gar als selbstverständlich betrachten. Im Gebiete der bloßen Mechanik ist die Unmöglichkeit des perpetuum mobile, d. h. der fortwährenden Produktion von Arbeit ohne bleibende Veränderung leicht darzuthun. Geht man also von der Ansicht aus, daß alle physikalischen Vorgänge lediglich mechanische Vorgänge, Bewegungen der Moleküle und Atome sind, so begreift man, auf Grund dieser mechanischen Auffassung der Physik, auch die Unmöglichkeit des perpetuum mobile in dem ganzen physikalischen Gebiet. Diese Auffassung zählt gegenwärtig wohl die meisten Anhänger. Andere Forscher lassen wieder nur eine durchaus experimentelle Begründung des Energiegesetzes gelten.

Es wird sich in dem Folgenden zeigen, daß alle berührten Momente bei Entwicklung der fraglichen Ansicht tatsächlich mitgewirkt haben, daß aber dabei außerdem ein bisher wenig beachtetes logisches und ein rein formales Bedürfnis eine ganz wesentliche Rolle gespielt hat.

1. Der Satz vom ausgeschlossenen perpetuum mobile.

Das Energiegesetz in seiner modernen Form ist zwar mit dem Satze vom ausgeschlossenen perpetuum mobile nicht identisch, doch steht es zu demselben in naher Beziehung. Letzterer Satz aber ist keineswegs neu, denn er hat auf mechanischem Gebiet schon vor Jahrhunderten die bedeutendsten Denker bei ihren Forschungen geleitet. Es sei gestattet, dies durch einige historische Beispiele zu begründen:

S. Stevinus, hypomnemata mathematica Tom. IV de statica. Leyden 1605 p. 34 beschäftigt sich mit dem Gleichgewicht auf der schiefen Ebene.

An einem dreiseitigen Prisma ABC (Fig. 44 im Durchschnitte dargestellt), dessen eine Seite AB horizontal ist, hängt eine geschlossene Schnur, an welcher sich 14 gleich schwere Kugeln gleichförmig verteilt befinden. Da man sich den untern symmetrischen Teil der Schnur ADC wegdenken kann, so schließt Stevin, daß die vier Kugeln auf AB den zwei Kugeln auf AC das Gleichgewicht halten. Denn wäre das Gleichgewicht in einem Momente gestört, so könnte es nie bestehen, die Schnur müßte immer in demselben Sinne kreisen, wir hätten ein perpetuum mobile.

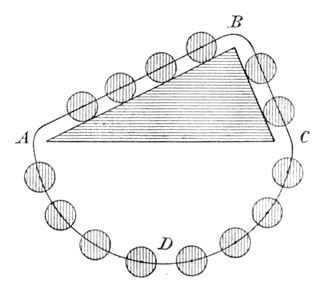
Fig. 44.

»Und gesetzt es sei dies, so würde die Reihe der Kugeln oder der Kranz (die Kette) dieselbe Lage haben wie zuvor, und aus demselben Grunde würden die acht Kugeln links gewichtiger sein, als jene sechs rechts; deshalb würden wieder jene acht sinken, jene sechs steigen, und diese Kugeln würden von selbst eine ewige Bewegung bewirken, was falsch ist.« »Atqui hoc si sit, globorum series sive corona eundem situm cum priore habebit, eademque de causa octo globi sinistri ponderosiores erunt sex dextris, ideoque rursus octo illi descendent, sex illi ascendent, istique globi ex sese continuum et aeternum motum efficient, quod est falsum.«

Hieraus leitet nun Stevin leicht die Gleichgewichtsgesetze für die schiefe Ebene und sehr viele andere fruchtbare Folgerungen ab.

In dem Abschnitt Hydrostatik desselben Werkes p. 114 stellt Stevin den Satz auf:

»Eine gegebene Wassermasse behält ihren gegebenen Ort innerhalb des Wassers.« »Aqusam datam, datum sibi intra aquam locum servare.«

Dieser Satz wird an Fig. 45 so bewiesen: » A also (wenn dies auf irgend eine natürliche Weise geschehen könnte) behalte den eingeräumten Ort nicht, sondern falle nach D: dies angenommen sinkt das A nachfolgende Wasser vermöge derselben Ursache nach D, und dasselbe wird wieder von anderem vertrieben, und so wird dieses Wasser (da dieselbe Ursache fortbesteht) eine beständige Bewegung eingehen, was absurd wäre.« » A igitur, (si ullo modo per naturam fieri possit) lacum sibi tributum non servato, ac delabatur in D; quibus positis aqua quae ipsi A succedit eandem ob causam deffluet in D, eademque ab alia instinc expelletur, atque adeo aqua haec (cum ubique eadem ratio sit) motum instituet perpetuum, quod absurdum fuerit.«

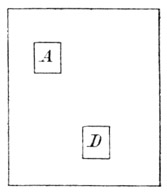
Fig. 45.

Hieraus werden nun sämtliche Sätze der Hydrostatik abgeleitet. Bei dieser Gelegenheit entwickelt Stevin auch zuerst den für die moderne analytische Mechanik so fruchtbaren Gedanken, nach welchem das Gleichgewicht eines Systems durch Hinzufügung fester Verbindungen nicht gestört wird. Bekanntlich leitet man heute z. B. den Satz der Erhaltung des Schwerpunktes aus dem D'Alembertschen Prinzipe mit Hilfe jener Bemerkung her.

Wenn wir gegenwärtig die Stevinschen Demonstrationen reproduzieren würden, so müßten wir sie freilich etwas verändern. Uns macht es keine Schwierigkeit bei hinweggedachten Widerständen die Kette auf seinem Prisma in endloser gleichförmiger Bewegung vorzustellen. Dagegen würden wir gegen die Annahme einer beschleunigten Bewegung oder auch gegen die einer gleichförmigen bei nicht beseitigten Widerständen protestieren. Auch ließe sich zur größeren Schärfe des Beweises die Kugelkette durch eine schwere gleichförmige vollkommen biegsame Schnur ersetzen.

Dies ändert nichts an dem historischen Wert der Stevinschen Betrachtungen. Es ist Tatsache, Stevin leitet anscheinend viel einfachere Wahrheiten aus dem Prinzip des unmöglichen perpetuum mobile ab.

In dem Gedankengang, welcher Galilei zu seinen Entdeckungen führt, spielt der Satz eine bedeutende Rolle, daß ein Körper durch die im Falle erlangte Geschwindigkeit gerade so hoch steigen kann, als er herabgefallen ist. Dieser Satz, der bei Galilei oft und mit großer Klarheit auftritt, ist doch nur eine andere Form des Prinzips vom ausgeschlossenen perpetuum mobile, wie wir dies bei Huygens sehen werden.

Galilei hat bekanntlich das Gesetz der gleichförmig beschleunigten Fallbewegung durch Spekulation als das »einfachste und natürlichste« gefunden, nachdem er zuvor ein anderes angenommen und wieder fallen gelassen hatte. Um aber sein Fallgesetz zu prüfen, stellte er Versuche über den Fall auf der schiefen Ebene an, wobei er die Fallzeiten durch die Gewichte des aus einem Gefäße in feinem Strahle ausfließenden Wassers bestimmte. Hierbei nimmt er nun als Grundsatz an, daß die auf der schiefen Ebene erlangte Geschwindigkeit immer der vertikalen Fallhöhe entspricht, was für ihn daraus hervorgeht, daß der auf einer schiefen Ebene gefallene Körper auf einer andern beliebig geneigten mit seiner Geschwindigkeit immer nur zur gleichen Vertikalhöhe aufsteigen kann. Der Satz über die Steighöhe hat ihn, wie es scheint, auch auf das Trägheitsgesetz geführt. Hören wir seine eigene geistvolle Auseinandersetzung im dialogo terzo. Opere. Padova 1744 Tom. III.

»Ich nehme an, die Geschwindigkeiten, welche dasselbe Bewegliche im Fall auf schiefen Ebenen verschiedener Neigung erreicht, seien gleich, wenn die vertikalen Fallhöhen gleich sind.« Accipio, gradus velocitatis ejusdem mobilis super diversas planorum inclinationes acquisitos tunc esse aequales, cum eorundem planorum elevationes aequales sint.«

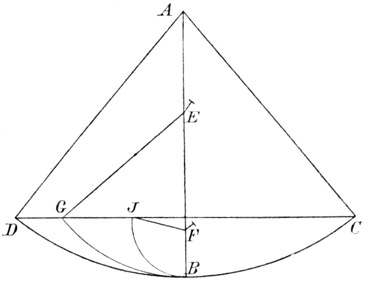
Fig. 46

»Ihr sprecht sehr überzeugend, aber über die Wahrscheinlichkeit hinaus will ich durch ein Experiment die Überzeugung so steigern, daß wenig zu einem strengen Beweis fehlen soll. Denkt Euch, dieses Blatt sei eine vertikale Wand, und an einem daselbst befestigten Nagel hänge an einem vertikalen Faden AB von 2 oder 3 Ellen eine Bleikugel von 1 oder 2 Unzen, und an der Wand zeichnet eine zu dem von der Wand ungefähr 2 Zolle entfernten AB senkrechte (horizontale) Gerade, führt Ihr dann den Faden AB mit der Kugel nach AC und laßt die Kugel frei, so seht Ihr dieselbe zunächst fallen, den Bogen CBD beschreibend, und so viel die Grenze B überschreiten, daß durch den Bogen BD laufend dieselbe fast zur Geraden CD aufsteigt, indem ein kleiner Zwischenraum übrig bleibt, so viel als vom Widerstand der Luft und des Fadens herrührt. Hieraus können wir schließen, daß der durch den Fall im Punkte B erlangte Schwung genügend sei, um durch einen gleichen Bogen zur selben Höhe aufzusteigen; nach wiederholter Ausführung des Versuches wollen wir in der Wand bei E einen Nagel einschlagen, oder bei F, 5 oder 6 Finger breit nach vorn, damit der Faden AC wenn er mit der Kugel wieder nach CB kommt und B erreicht, beim Nagel E festgehalten, und die Kugel genötigt werde, den Bogen BC um E zu beschreiben, wobei wir sehen werden, was dieselbe Geschwindigkeit leistet, die vorher denselben Körper durch den Bogen BD zur Horizontalen CD beförderte. Nun, meine Herren, werdet Ihr mit Vergnügen bemerken, daß die Kugel im Punkte G den Horizont erreicht, und dasselbe geschieht, wenn das Hindernis sich tiefer befindet, wie bei E, wobei die Kugel den Bogen BJ beschreibt, den Aufstieg stets im Horizont CD beendend, und wenn der hemmende Nagel so tief läge, daß der Rest des Fadens nicht mehr den Horizont CD erreichen kann (was eintritt, wenn er näher an B als am Durchschnitt von AB mit CD liegt), so überhüpft der Faden den Nagel und wickelt sich herum. Dieser Versuch läßt keinen Zweifel über die Wahrheit des aufgestellten Satzes. Denn, da die Bögen CB, DB einander gleich sind und symmetrisch liegen, so wird das beim Fall durch den Bogen CB erlangte Moment ebenso groß sein, wie die Wirkung durch den Bogen DB; aber das in B erlangte, durch CB hindurch erzeugte Moment vermag denselben Körper durch den Bogen BD zu heben; folglich wird auch das beim Sinken durch DB erzeugte Moment gleich sein demjenigen, welches denselben Körper vorher von B bis D führen konnte, so daß allgemein jedes beim Sinken erzeugte Moment gleich demjenigen ist, welches den Körper durch denselben Bogen zu erheben im stande ist: aber alle Momente, die den Körper durch die Bögen BD, BG, BJ heben konnten, sind einander gleich, da sie stets im Fall durch CB entstanden waren, wie der Versuch lehrt: folglich sind auch alle Momente, welche im Fall durch die Bögen DB, GB, JB entstehen, einander gleich.« Voi molto probabilmente discorrete, ma oltre al veri simile voglio con una esperienza crescer tanto la probabilità, che poco gli manchi all' agguagliarsi ad una ben necessaria dimostrazione. Figuratevi questo foglio essere una parete eretta al orizzonte, e da un chiodo fitto in essa pendere una palla di piombo d'un'oncia, o due, sospesa dal sottil filo AB lungo due, o tre braccia perpendicolare all' orizzonte, e nella parete segnate una linea orizzontale DC segante a squadra il perpendicolo AB, il quale sia lontano dalla parete due dita in circa, trasferendo poi il filo AB colla palla in AC, lasciata essa palla in libertà, la quale primieramente vedrete scendere descrivendo l'arco CBD, e di tanto trapassare il termine B, che scorrendo per l'arco BD, sormonterà fino quasi alla segnata parallela CD, restando di per vernirvi per piccolissimo intervallo toltogli il precisamente arrivarvi dall' impedimento dell'aria, e del filo. Dal che possiamo veracemente concludere, che l'impeto acquistato nel punto B dalla palla nello scendere per l'arco CB, fu tanto, che bastò a risospingersi per un simile arco BD alla medesima altezza; fatta, e più volte reiterata cotale esperienza, voglio, che fiechiamo nella parete rasente al perpendicolo AB un chiodo come in E ovvero in F, che sporga in fuori cinque, o sei dita, e questo acciocchè il filo AC tornando come prima a riportar la palla C per l'arco CD, giunta che ella sia in B, intoppando il filo nel chiodo E, sia costretta a camminare per la circonferenza BG descritta intorno al centro E, dal che vedremo quello, che potrà far quel medesimo impeto, che dianzi concepito nel medesimo termine B, sospinse l'istesso mobile per l'arco ED all'altezza dell'orizzontale CD. Ora, Signori, voi vedrete con gusto condursi la palla all'orizzontale nel punto G, e l'istesso accadere, l'intoppo si metesse più basso come in F, dove la palla descriverebbe l'arco BJ, terminando sempre la sua salita precisamente nella linea CD, e quando l'intoppo del chiodo fusse tanto basso, che l'avanzo del filo sotto di lui non arivasse all' altezza di CD (il che accaderebbe, quando fusse più vicino al punto B, che al segamento dell' AB coli' orizzontale CD), allora il filo cavalcherebbe il chiodo, e segli avolgerebbe intorno. Questa esperienza non lascia luogo di dubitare della verità del supposto: imperocchè essendo il due archi CB, DB equali e similmento posti, l'acquisto di momento fatto per la scesa nell'arco CB è il medesimo, che il fatto per la scesa dell'arco DB: ma il momento acquistato in B per l'arco CB è potente a risospingere in su il medesimo mobile per l'arco BD; adunque anco il momento acquistato nella scesa DB è eguale a quello, che sospigne l'istesso mobile pel medesimo arco da B in D, sicche universalmente ogni momento acquistato per la scesa dun arco è eguale a quello, che può far risalire l'istesso mobile pel medisimo arco: ma i momenti tutti che fanno risalire per tutti gli archi BD, BG, BJ sono eguali, poichè son fatti dal istesso medesimo momento acquistato per la scesa CB, come mostra l'esperienza: adunque tutti i momenti, che si acquistano per le scese negli archi JB, CB, JB sono eguali.

Die über das Pendel gemachte Bemerkung überträgt sich sofort auf die schiefe Ebene und führt zum Trägheitsgesetz. Es heißt S. 124:

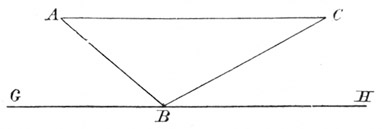
Fig. 47

»Es steht bereits fest, daß ein Bewegliches aus der Ruhe in A durch AB herabsteigend dem Zeitzuwachs entsprechende (Geschwindigkeiten erlangt: daß aber der Geschwindigkeitsgrad in B der größte und unveränderlich eingepflanzt sei, wenn nämlich die Ursache einer neuen Beschleunigung oder Verzögerung beseitigt ist: einer Beschleunigung, sage ich, wenn dasselbe weiter auf der ausgedehnten Ebene fortschreitet; einer Verzögerung aber, wenn es auf die ansteigende Ebene BC abgeleitet wird: auf der Horizontalen GH aber wird die gleichförmige Bewegung je nach der von A nach B erlangten Geschwindigkeit ins Unendliche fortbestehen.« Constat jam, quod mobile ex quiete in A descendens per AB, gradus acquirit velocitatis juxta temporis ipsius incrementum: gradum vero in B esse maximum acquisitorum, et suapte natura imutabiliter impressum, sublatis scilicet ¦causis accelerationis novae, aut retardationis: accelerationis inquam, si adhuc super extenso piano ulterius progrederetur; retardationis vero, dum super planum acclive BC fit reflexio: in horizontali autem GH aequabilis motus juxta gradum velocitatis ex A in B acquisitae in infinitum extenderetur.

Huygens, in allen Stücken ein Nachfolger Galileis, faßt das Trägheitsgesetz schärfer und verallgemeinert den für Galilei so fruchtbar gewordenen Satz über die Steighöhe. Letzteren verwendet er zur Lösung des Problems vom Schwingungsmittelpunkt und spricht sich darüber vollkommen klar aus, daß der Satz über die Steighöhe identisch sei mit dem Satze vom ausgeschlossenen perpetuum mobile.

»Wenn die Schwere nicht wäre, und wenn die Luft die Bewegung der Körper nicht hindern würde, würde jeder derselben die einmal angenommene Bewegung mit gleich bleibender Geschwindigkeit längs einer geraden Linie fortsetzen.« Si gravitas non esset, neque aër motui corporum ofiiceret, unumquodque eorum, acceptum semel motum continuaturum velocitate aequabili, secundum lineam rectam.

»Wenn beliebige schwere Körper durch ihr Gewicht in Bewegung geraten, kann der gemeinsame Schwerpunkt derselben nicht höher steigen, als er zu Anfang sich befand.«

»Wir werden zeigen, daß diese Voraussetzung, obgleich sie bedenklich scheinen könnte, nichts anderes besagt als das, was nie jemand bezweifelt hat, daß die schweren Körper sich nicht (von selbst) aufwärts bewegen. – Und wenn dies die Erfinder neuer Konstruktionen zu benützen verständen, welche in irrigem Streben ein perpetuum mobile herzustellen suchen, würden sie leicht ihre Fehler erkennen und einsehen, daß diese Sache auf mechanischem Wege nicht möglich sei.« Horologii pars quarta. De centro oscillationis:
Sie pondera quotlibet, vi gravitatis suae, moveri incipiant; non posse centrum gravitatis ex ipsis compositae altius, quam ubi incipiente motu reperiebatur, ascendere.
Ipsa vero hypothesis nostra quominus scrupulum moveat, nihil aliud sibi velle ostendemus, quam quod nemo unquam negavit, gravia nempe sursum non ferri. – Et sane, si hac eadem uti scirent novorum operum machinatores, qui motum perpetuum irrito conatu moliuntur, facile suos ipsi errores deprehenderent, intelligerentque rem eam mechanica ratione haud quaquam possibilem esse.

Eine jesuitische reservatio mentalis ist vielleicht in den Worten »mechanica ratione« angedeutet. Man könnte hiernach glauben, daß Huygens ein nichtmechanisches perpetuum mobile für möglich hält.

Klarer wird die Verallgemeinerung des Galileischen Satzes noch in Propos. IV desselben Abschnittes ausgesprochen:

»Wenn ein beliebiges aus mehreren schweren Körpern bestehendes Pendel aus der Ruhe freigelassen einen beliebigen Teil einer Schwingung ausgeführt hat, und man denkt sich nachher bei aufgelösten Verbindungen die Geschwindigkeiten aufwärts gekehrt, und die Körper so hoch als möglich aufgestiegen, so wird, nachdem dies geschehen, der gemeinsame Schwerpunkt so hoch gestiegen sein, als derselbe sich zu Anfang der Bewegung befand.« Si pendulum e pluribus ponderibus compositum, atque e quiete dimissum, partem quamcunque oscillationis integrae confecerit, atque inde porro intelligantur pondera ejus singula, relicto communi vinculo, celeritates acquisitas sursum convertere, ac quousque possunt ascendere; hoc facto centrum gravitatis ex omnibus compositae, ad eandem altitudinem reversum erit, quam ante inceptam oscillationem obtinebat.

Auf letzteren Satz nun, welcher eine Verallgemeinerung ist des von Galilei für eine Masse aufgestellten für ein System von Massen, und den man nach der Huygensschen Erläuterung als das Prinzip des ausgeschlossenen perpetuum mobile erkennt, gründet Huygens die Theorie des Schwingungsmittelpunktes. Lagrange nennt dieses Prinzip prekär und freut sich, daß es Jakob Bernoulli 1681 gelungen sei, die Theorie des Schwingungsmittelpunktes auf die Hebelgesetze zurückzuführen, die ihm klarer scheinen. An demselben Problem versuchen sich fast alle bedeutenden Forscher des 17. und 18. Jahrhunderts, und es führt zuletzt in Vereinigung mit dem Prinzip der virtuellen Geschwindigkeit zu dem von D' Alembert (traité de dynamique 1743) aufgestellten, vorher schon in etwas anderer Form von Euler und Hermann verwendeten Prinzip.

Außerdem wird der Huygenssche Satz über die Steighöhe zur Grundlage des Gesetzes der Erhaltung der lebendigen Kraft und des Satzes der Erhaltung der Kraft überhaupt, wie er von Joh. und Dan. Bernoulli aufgestellt und namentlich von letzterem in seiner Hydrodynamik so fruchtbar verwendet wird. Diese Bernoullischen Sätze unterscheiden sich nur in der Form des Ausdruckes von der späteren Lagrangeschen Aufstellung.

Die Art, wie Torricelli sein berühmtes Ausflußtheorem für Flüssigkeiten gefunden hat, führt wieder auf denselben Satz. Torricelli nahm an, daß die aus der Bodenöffnung des Gefäßes strömende Flüssigkeit vermöge ihrer Ausflußgeschwindigkeit nicht höher steigen könne, als sie im Gefäße steht.

Betrachten wir noch einen der reinen Mechanik angehörigen Punkt, die Geschichte des Prinzips der virtuellen Bewegung. Das Prinzip wurde nicht, wie man gewöhnlich sagt, und wie auch Lagrange behauptet, von Galilei, sondern jedenfalls schon früher von Stevin aufgestellt. In seiner Trochleostatica des oben zitierten Werkes p. 172 sagt er:

»Es sei bemerkt, daß hier das statische Axiom gelte: Wie der Weg des Wirkenden zum Weg des Leidenden, So die Kraft des Leidenden zur Kraft des Wirkenden.« »Notare autem hic illud staticum axioma etiam locum habere:

»Ut spatium agentis ad spatium patientis Sic potentia patientis ad potentiam agentis.«

Galilei bemerkt, wie bekannt, die Giltigkeit des Prinzipes bei Betrachtung der einfachen Maschinen und leitet auch die Gleichgewichtsgesetze der Flüssigkeiten aus demselben ab.

Torricelli führt das Prinzip auf Schwerpunkteigenschaften zurück. Soll an einer einfachen Maschine, an welcher wir uns Kraft und Last durch angehängte Gewichte vertreten denken, Gleichgewicht bestehen, so darf der gemeinsame Schwerpunkt der aufgelegten Lasten nicht sinken. Umgekehrt, wenn der Schwerpunkt nicht sinken kann, besteht Gleichgewicht, weil die schweren Körper nicht von selbst aufwärts steigen. In dieser Form ist also das Prinzip der virtuellen Geschwindigkeit identisch mit dem Huygensschen Prinzip der Unmöglichkeit des Perpetuum mobile.

Joh. Bernoulli erkennt zuerst 1717 in einem Briefe an Varignon die allgemeine Bedeutung des Prinzipes der virtuellen Bewegung für beliebige Systeme.

Lagrange endlich gibt einen allgemeinen Beweis des Prinzipes und gründet darauf seine ganze analytische Mechanik. Aber dieser allgemeine Beweis stützt sich im Grunde doch nur auf die Huygenssche und Torricellische Bemerkung.

Lagrange denkt sich bekanntlich in den Richtungen der am System wirksamen Kräfte eine Art einfacher Flaschenzüge, windet eine Schnur durch alle diese Flaschenzüge durch, und hängt schließlich am Ende derselben eine Last an, welche ein gemeinschaftliches Maß sämtlicher am System wirksamer Kräfte ist. Die Elementenzahl jedes einzelnen Flaschenzuges kann nun leicht so gewählt werden, daß die betreffende Kraft in der Tat durch denselben ersetzt wird. Dann ist es klar, daß, wenn die angehängte Endlast nicht sinken kann, Gleichgewicht besteht, weil schwere Körper nicht von selbst aufwärts steigen.

Wenn man nicht so weit geht, sondern der Torricellischen Betrachtung näher bleiben will, so kann man sich jede Einzelkraft des Systems durch eine besondere Last ersetzt denken, die an einer Schnur hängt, welche über eine in der Richtung der Kraft liegende Rolle führt und am Angriffspunkte der Kraft befestigt ist. Gleichgewicht besteht dann, wenn der gemeinsame Schwerpunkt der sämtlichen Lasten nicht sinken kann. Die Grundannahme dieses Beweises ist offenbar die Unmöglichkeit des perpetuum mobile.

Lagrange hat sich vielfach bemüht, einen von fremdartigen Elementen freien und vollständig befriedigenden Beweis zu liefern, ohne daß ihm dies ganz gelungen wäre. Auch andere nach ihm dürften nicht glücklicher gewesen sein.

So ruht nun die ganze Mechanik auf einem Gedanken, der, wenn auch nicht zweifelhaft, so doch fremdartig und den übrigen Grundsätzen und Axiomen der Mechanik nicht ebenbürtig scheint. Jeder, der Mechanik treibt, fühlt einmal die Unbehaglichkeit dieses Zustandes, jeder wünscht sie beseitigt, selten wird sie durch Worte ausgedrückt. Und so findet sich der strebsame Jünger der Wissenschaft hoch erfreut, wenn er einmal bei einem Meister wie Poinsot in seiner »théorie général de l'équilibre et du mouvement des systèmes« folgende Stelle liest, in welcher er sich über die analytische Mechanik ausspricht:

»Indessen, da man in diesem Werke von Anfang an nur daran dachte, die schöne Entwicklung der Mechanik zu betrachten, welche ganz aus einer Formel zu fließen schien, glaubte man natürlich, daß die Wissenschaft fertig sei, und daß nichts übrig sei, als das Prinzip der virtuellen Geschwindigkeiten zu beweisen. Aber diese Untersuchung brachte alle Schwierigkeiten zurück, welche man eben durch das Prinzip überwunden hatte. Dieses allgemeine Gesetz, in welches sich verschwommene Ideen von unendlich kleinen Bewegungen und Gleichgewichtsstörungen einmengen, verdunkelte sich gewissermaßen bei näherer Prüfung; und da das Buch von Lagrange keine Klarheit mehr zeigte als in dem Gang der Rechnungen, sah man bald, daß das Gewölke über den Entwicklungen nur darum gehoben schien, weil es gewissermaßen über den Anfängen dieser Wissenschaft gesammelt war.«

»Der allgemeine Beweis des Prinzipes der virtuellen Geschwindigkeiten kommt eigentlich darauf hinaus, die ganze Mechanik auf einer andern Grundlage aufzubauen: Denn der Beweis eines Gesetzes, welches die ganze Wissenschaft umfaßt, kann nichts anderes sein, als die Zurückführung dieser Wissenschaft auf ein anderes ebenso allgemeines aber einleuchtendes oder wenigstens einfacheres Gesetz, welches also das erstere unnötig macht.« »Cependant, comme dans cet ouvrage on ne fut d'abord attentif qu'à considérer ce beau développement de la mécanique qui semblait sortir tout entière d'une seule et même formule, ou crut naturellement que la science était faite, et qu'il ne restait plus qu'à chercher la démonstration du principe des vitesses virtuelles. Mais cette recherche ramena toutes les difficultés qu'on avait franchies par le principe même. Cette loi si générale, où se mêlent des idées vagues et étrangères de mouvements infinement petits et de perturbation d'équilibre, ne fit en quelque sorte que s'obsurcir à l'examen: et le livre de Lagrange n'offrant plus alors rien de clair que la marche des calculs, on vit bien que les nuages n'avaient paru levé sur le cours de la mécanique que parcequ'ils étaient, pour ainsi dire, rassemblés à l'origine même de cette science.

Une démonstration générale du principe des vitesses virtuelles devait au fond revenir à établir la mécanique entière sur une autre base: car la démonstration d'une loi qui embrasse toute une science ne peut être autre chose que la réduction de cette science à une autre loi aussi générale, mais évidente, ou du moins plus simple que la première, et qui partam la rende inutile.«

Das Prinzip der virtuellen Bewegung beweisen heißt also nach Poinsot die ganze Mechanik neu machen.

Ein anderer dem Mathematiker unbehaglicher Umstand ist der, daß in dem historischen Zustande, in welchem sich die Mechanik gegenwärtig befindet, die Dynamik sich auf die Statik gründet, während man doch wünschen muß, daß in einer Wissenschaft, die auf deduktive Vollendung Anspruch macht, die spezielleren statischen Sätze sich mit Leichtigkeit aus den allgemeineren dynamischen ableiten lassen.

Diesem Wunsche gibt auch wieder ein großer Meister, nämlich Gauss, Ausdruck bei Gelegenheit der Aufstellung seines Prinzipes des kleinsten Zwanges (Crelles Journal IV. Bd. S. 233) mit folgenden Worten: »So sehr es in der Ordnung ist, daß bei der allmählichen Ausbildung der Wissenschaft und bei der Belehrung des Individuums das Leichtere dem Schwerern, das Einfachere dem Verwickeltern, das Besondere dem Allgemeinen vorangeht, so fordert doch der Geist, einmal auf dem höhern Standpunkt angelangt, den umgekehrten Gang, wobei die ganze Statik nur als ein spezieller Fall der Mechanik erscheine.« Das Gausssche Prinzip ist nun allerdings ein allgemeines, nur schade, daß es nicht unmittelbar einzusehen, und daß Gauss es wieder mit Hilfe des D'Alembertschen Prinzips abgeleitet hat, wodurch alles wieder beim Alten bleibt.

Woher kommt nun diese sonderbare Rolle, die das Prinzip der virtuellen Bewegung in der Mechanik spielt? Ich will vorläufig nur dies darauf antworten. Es würde mir schwer fallen, die Verschiedenheit des Eindruckes zu beschreiben, den der Lagrangesche Beweis des Prinzipes auf mich machte, als ich ihn das erstemal als Student, und als ich ihn später wieder vornahm, nachdem ich historische Studien gemacht hatte. Früher erschien mir der Beweis abgeschmackt, namentlich durch seine Rollen und Schnüre, die mir nicht in die mathematische Betrachtung paßten, und deren Wirkung ich lieber aus dem Prinzipe selbst erkannt hätte, statt sie als bekannt vorauszusetzen. Nachdem ich aber die Geschichte studiert, kann ich mir keine schönere Ableitung denken.

In der Tat ist es durch die ganze Mechanik dasselbe Prinzip des ausgeschlossenen perpetuum mobile, welches fast alles verrichtet, das Lagrange mißfällt, und das er doch selbst bei seiner Ableitung wenigstens versteckt benützen muß. Geben wir diesem Prinzip seine richtige Stellung und Fassung, so wird das Paradoxe natürlich.

Das Prinzip des ausgeschlossenen perpetuum mobile ist also gewiß keine neue Entdeckung; es leitet seit 300 Jahren die größten Forscher. Das Prinzip kann sich aber auch nicht eigentlich auf mechanische Einsichten gründen. Denn lange vor dem Ausbau der Mechanik besteht schon die Überzeugung von der Richtigkeit desselben, und diese wirkt eben bei dem Ausbau mit. Diese überzeugende Kraft muß also allgemeinere und tiefere Wurzeln haben. Wir kommen auf diesen Punkt zurück.

2. Die mechanische Physik.

Es kann nicht in Abrede gestellt werden, daß von Demokrit an bis auf die neueste Zeit ein unverkennbares Streben nach einer mechanischen Erklärung aller physikalischen Vorgänge besteht. Sehen wir von älteren unklaren Äußerungen auch ganz ab, so lesen wir doch bei Huygens Traité de la lumière. A Leide 1690 p. 2. folgendes:

»Man darf nicht daran zweifeln, daß das Licht in der Bewegung irgend eines Stoffes besteht. Denn sei es, daß man seine Entstehung betrachtet, so findet man, daß es hier auf Erden vorzüglich durch Feuer und Flamme erzeugt wird, welche ohne Zweifel Körper in heftiger Bewegung enthalten, weil sie mehrere der härtesten Körper auflösen und schmelzen; sei es, daß man dessen Wirkungen betrachtet, so sieht man, daß das durch Hohlspiegel gesammelte Licht die Fähigkeit hat, wie Feuer zu brennen, d. h. daß es die Teile der Körper trennt, was sicherlich eine Bewegung andeutet, wenigstens in der wahren Philosophie, welche alle natürlichen Wirkungen auf mechanische Ursachen zurückführt. Denn das muß nach meiner Meinung geschehen, wenn man nicht jede Hoffnung, etwas in der Physik zu begreifen, aufgeben will.« L'on ne sçaurait douter que la lumière ne consiste dans le mouvement de certaine matiere. Car soit qu'on regarde sa production, on trouve qu'içy sur la terre c'est principalement le feu et la flamme qui l'engendrent, lesquels contient sans doute des corps qui sont dans un mouvement rapide, puis qu'ils dissolvent et fondent plusieurs autres corps des plus solides: soit qu'on regarde ses effets, on voit que quand la lumière est ramassée, comme par des miroires concaves, elle a la vertu de brûler comme le feu, c'est-à-dire qu'elle desunit les parties des corps; ce qui marque assurément du mouvement, au moins dans la vraye Philosophie, dans laquelle on conçoit la cause de tous les effets naturels par des raisons de mechanique. Ce qu'il faut faire à mon avis, ou bien renoncer à toute espérance de jamais rien comprendre dans la Physique.

S. Carnot, Sur la puissance motrice du feu. Paris 1824.indem er das Prinzip des ausgeschlossenen perpetuum mobile in die Wärmelehre einführt, entschuldigt sich folgendermaßen:

»Man wird vielleicht einwenden, daß das perpetuum mobile, welches nur für mechanische Vorgänge als unmöglich erwiesen ist, bei Anwendung von Wärme oder Elektrizität vielleicht möglich ist; aber kann man denn die Erscheinungen der Wärme oder der Elektrizität als etwas anderes auffassen, denn als Bewegungen gewisser Körper, und müssen sie als solche nicht den allgemeinen Gesetzen der Mechanik genügen?« »On objectra peut-être ici que le mouvement perpétuel, démontré impossible par les seules actions mécaniques, ne l'est peut-être pas lorsqu'on emploie l'influence soit de la chaleur, soit de électricité; mais peut-on concevoir les phénomènes de la chaleur et de électricité comme dus à autre chose qu'à des mouvements quelconques des corps, et comme tels ne doivent-ils pas être soumis aux lois générales de la mécanique?«

Diese Beispiele, welche sich durch Citate aus der neuesten Zeit ins Endlose vermehren ließen, zeigen, daß ein Streben, alles mechanisch aufzufassen, wirklich besteht. Und dieses Streben ist auch erklärlich. Die mechanischen Vorgänge als einfache Bewegungen in Raum und Zeit sind der Beobachtung und Verfolgung mit Hilfe unserer höchst organisierten Sinne am besten zugänglich. Die mechanischen Vorgänge reproduzieren wir fast mühelos in unserer Phantasie. Der Druck als bewegungseinleitender Umstand ist uns aus täglicher Übung wohl bekannt. Alle Änderungen, welche das Individuum persönlich in seiner Umgebung, oder die Menschheit auf dem Wege der Technik in der Welt hervorbringt, sind durch Bewegungen vermittelt. Wie sollte uns also die Bewegung nicht als der wichtigste physikalische Faktor erscheinen?

Es gelingt auch an allen physikalischen Vorgängen mechanische Eigenschaften zu entdecken. Die tönende Glocke zittert, der erhitzte Körper dehnt sich aus, der elektrische Körper zieht andere an. Warum sollte man also nicht versuchen, alle Vorgänge bei der uns geläufigsten, der Beobachtung und Messung leichter zugänglichen mechanischen Seite zu fassen? Es ist auch nichts gegen den Versuch einzuwenden, die mechanischen Eigenschaften der physikalischen Vorgänge durch mechanische Analogien zu erläutern.

Die moderne Physik ist aber in dieser Richtung allerdings sehr weit gegangen. Der Standpunkt, den Wundt in seiner sehr ansprechenden Schrift »über die physikalischen Axiome« zum Ausdruck bringt, möchte wohl von der Mehrzahl der Physiker geteilt werden.

Man könnte sich mit diesen Sätzen als Grundsätzen der Mechanik befreunden. Wenn dieselben aber als Axiome der Physik aufgestellt werden, so entspricht dies eigentlich einer Negierung aller Vorgänge mit Ausnahme der Bewegung. Alle Veränderungen in der Natur sind nach Wundt bloße Ortsveränderungen, alle Ursachen sind Bewegungsursachen (a. a. O. S. 26). Wollten wir auf die philosophische Begründung, die Wundt für seine Ansicht gibt, eingehen, so würde uns dies tief in die Spekulationen der Eleaten und Herbartianer hineinführen. Die Ortsveränderung, meint Wundt, sei die einzige Veränderung eines Dinges, wobei dieses identisch bleibt. Ändert sich ein Ding qualitativ, so müßte man sich vielmehr vorstellen, daß ein Ding vergeht und ein anderes entsteht, was mit der Vorstellung von der Identität des beobachteten Wesens und von der Unzerstörbarkeit der Materie nicht zusammenzureimen ist. Wir brauchen uns aber nur zu erinnern, daß die Eleaten Schwierigkeiten ganz derselben Art in der Bewegung gefunden haben. Kann man denn nicht auch denken, daß ein Ding an einem Orte vergeht und an einem andern ein gleiches entsteht?

Wissen wir denn im Grunde genommen mehr davon, warum ein Körper einen Ort verläßt und an einem andern auftaucht, als wie so ein kalter Körper warm wird? Gesetzt auch, wir verstünden die mechanischen Vorgänge vollständig, könnten und dürften wir deshalb andere Vorgänge, die wir nicht verstehen, aus der Welt schaffen? Nach diesem Prinzipe wäre es wirklich das Einfachste, die Existenz der ganzen Welt zu leugnen. Die Eleaten sind eigentlich dahin gelangt, und die Herbartianer waren nicht weit von diesem Ziel.

Die Physik, in dieser Weise behandelt, liefert uns nun ein Schema, in dem wir die wirkliche Welt kaum wieder erkennen. Und in der That erscheint Menschen, welche sich dieser Ansicht durch einige Jahre hingegeben haben, die Sinnenwelt, von welcher, als einer wohl vertrauten Sache, sie ausgegangen waren, plötzlich als das größte – – »Welträtsel.«

So erklärlich es also auch ist, daß man bestrebt war, alle physikalischen Vorgänge »auf Bewegungen der Atome zurückzuführen,« so muß man doch sagen, daß dies ein chimärisches Ideal ist. Dasselbe hat in populären Vorlesungen oft als effektvolles Programm gedient. In dem Arbeitsraume des ernsten Forschers hat es kaum eine wesentliche Funktion gehabt.

Was in mechanischer Physik wirklich geleistet worden ist, besteht entweder in Erläuterung physikalischer Vorgänge durch uns geläufigere mechanische Analogien, wofür die Theorien des Lichtes und der Elektrizität, oder in der genauen quantitativen Ermittelung des Zusammenhanges mechanischer Vorgänge mit andern physikalischen Prozessen, wofür die der Thermodynamik angehörigen Arbeiten Beispiele bieten.

3. Das Energieprinzip in der Physik.

Nur die Erfahrung kann uns darüber belehren, daß durch mechanische Vorgänge andere physikalische Wandlungen bedingt sind, und umgekehrt. Durch die Erfindung der Dampfmaschine und deren technische Bedeutung wurde die Aufmerksamkeit zuerst auf den Zusammenhang mechanischer Vorgänge (insbesondere der Arbeitsleistung) mit Wärmezustandsänderungen gelenkt. Das technische Interesse mit dem Bedürfnisse nach wissenschaftlicher Klarheit vereinigten sich in dem Kopfe von S. Carnot, und führten zu der merkwürdigen Entwicklung, deren Ergebnis die Thermodynamik ist. Es ist nur ein historischer Zufall, daß diese Gedankenentwickelung nicht an die Elektrotechnik anknüpfen konnte.

Bei der Untersuchung darüber, wie viel Arbeit im Maximum eine Wärmemaschine überhaupt, und eine Dampfmaschine insbesondere, mit einem bestimmten Aufwand an Verbrennungswärme leisten kann, läßt sich Carnot durch mechanische Analogien leiten. Ein Körper kann Arbeit leisten, indem er sich durch Erwärmung unter Druck ausdehnt. Hierzu muß derselbe aber von einem wärmeren Körper Wärme empfangen. Die Wärme muß also, um Arbeit zu leisten, von einem wärmeren zu einem kälteren Körper übergehn, ebenso wie das Wasser von einem höheren Niveau auf ein tiefes sinken muß, um die Mühle in Bewegung zu setzen. Temperaturdifferenzen stellen also ebenso Arbeitskräfte vor wie Höhendifferenzen schwerer Körper.

Carnot erdenkt einen idealen Prozeß, bei welchem gar keine Wärme nutzlos (ohne Arbeitsleistung) abfließt. Dieser liefert also mit gegebenem Wärmeaufwand das Arbeits maximum. Das Analogon ist ein Mühlrad, welches auf einem höheren Niveau Wasser schöpft, das in demselben ohne einen Tropfen Verlust sehr langsam auf ein tieferes Niveau herabsinkt. Der Prozeß hat das Eigentümliche, daß mit dem Aufwand derselben Arbeitsleistung das Wasser wieder genau auf die ursprüngliche Höhe geschafft werden kann. Diese Eigenschaft der Umkehrbarkeit kommt auch dem Carnotschen Prozeß zu. Auch dieser kann bei Aufwand derselben Arbeitsleistung umgekehrt, und hierbei die Wärme wieder auf das ursprüngliche Temperaturniveau geschafft werden.

Würde es zwei verschiedene umkehrbare Prozesse A, B geben, derart, daß in A eine von der Temperatur t ₁ auf die niedere Temperatur t ₂ abfließende Wärmemenge Q eine Arbeit W, in B aber unter denselben Umständen eine größere Arbeit W + Wxxxsup>1xxx/sup> ergäbe, so könnte man B im angegebenen Sinne und A im umgekehrten Sinne zu einem Prozeß verbinden. Hierbei würde A die durch B herbeigeführte Wärmeänderung rückgängig machen, und einen sozusagen aus nichts gewonnenen Arbeitsüberschuß Wxxxsup>1xxx/sup> übrig lassen. Diese Kombination würde ein perpetuum mobile vorstellen.

In dem Gefühl nun, daß wenig darauf ankommt, ob die mechanischen Gesetze unmittelbar oder auf einem Umwege (durch Wärmevorgänge) durchbrochen werden, in der Überzeugung von dem allgemeinen gesetzmäßigen Naturzusammenhang, schließt hier Carnot zum erstenmal auf dem Gebiet der allgemeinen Physik das perpetuum mobile aus. Dann aber kann die Arbeitsgröße W, welche durch Übergang von einer Wärmemenge Q von t ₁ auf t ₂ gewonnen werden kann, gar nicht von der Natur der Stoffe und auch nicht von der Art des Prozesses (sofern derselbe nur verlustlos), sondern nur von den Temperaturen t ₁ und t ₂ abhängen.

Dieser wichtige Satz ist durch die Spezialuntersuchungen von Carnot selbst (1824), von Clapeyron (1834) und von William Thomson (1849) aufs vollständigste bestätigt worden. Derselbe ist ohne irgend eine Annahme über die Natur der Wärme durch Ausschluß des perpetuum mobile gewonnen. Carnot hat allerdings die Blacksche Ansicht festgehalten, nach welcher die gesamte Wärmemenge unveränderlich ist, doch ist, soweit die Untersuchung bisher betrachtet wurde, die Entscheidung hierüber belanglos. Schon der Carnotsche Satz hat zu den merkwürdigsten Ergebnissen geführt. W. Thomson (Lord Kelvin) (1848) hat auf denselben den genialen Gedanken einer absoluten (allgemein vergleichbaren) Temperaturskala gegründet. James Thomson (1849) hat sich einen Carnotschen Prozeß mit unter Druck frierendem und daher Arbeit leistendem Wasser vorgestellt. Er hat hierbei erkannt, daß durch den Druck je einer Atmosphäre der Gefrierpunkt um 0.0075° Celsius erniedrigt wird. Dies sei nur als Beispiel erwähnt.

Zwei Dezennien nach Carnots Publikation wurde durch J. R. Mayer und J. P. Joule ein weiterer Fortschritt herbeigeführt. Mayer beobachtete als Arzt in holländischen Diensten bei Gelegenheit von Aderlässen auf Java eine auffallende Röte des venösen Blutes. Er brachte dies nach Liebigs Theorie der animalen Wärme mit dem geringeren Wärmeverlust in dem wärmeren Klima und mit dem geringeren Verbrauch an organischem Brennstoff in Zusammenhang. Die gesamte Wärmeausgabe eines sich ruhig verhaltenden Menschen mußte der gesamten Verbrennungswärme entsprechen. Da aber alle organischen Leistungen, auch die mechanischen, auf Rechnung der Verbrennungswärme gesetzt werden mußten, so mußte eine Beziehung zwischen mechanischer Leistung und Wärmeverbrauch bestehen.

Joule ging von ganz ähnlichen Überlegungen über die galvanische Batterie aus. Die dem Zinkverbrauch entsprechende Verbindungswärme kann in der galvanischen Zelle zum Vorschein kommen. Kommt ein Strom zu Stande, so tritt ein Teil dieser Wärme in dem Stromleiter auf. Ein eingeschalteter Wasserzersetzungsapparat bringt einen Teil dieser Wärme zum Verschwinden; dieselbe kommt aber bei Verbrennung des gebildeten Knallgases wieder zum Vorschein. Treibt der Strom einen Elektromotor, so verschwindet wieder ein Teil der Wärme, der aber bei Aufzehrung der Arbeit durch Reibung wieder zum Vorschein kommt. Auch Joule erscheint also sowohl die erzeugte Wärme als auch die erzeugte Arbeit an einen Stoff verbrauch gebunden. Es liegt demnach sowohl Mayer als Joule nahe, Wärme und Arbeit als gleichartige Größen anzusehen, welche so zusammenhängen, daß stets in der einen Form zum Vorschein kommt, was in der andern verschwindet. Es geht daraus eine substanzielle Auffassung der Wärme und der Arbeit hervor, und schließlich eine substanzielle Auffassung der Energie überhaupt. Hierbei wird als Energie jede physikalische Zustandsänderung angesehen, deren Vernichtung Arbeit (oder äquivalente Wärme) erzeugt. Elektrische Ladung z. B. ist Energie.

Mayer hat (1842) aus den damals allgemein bekannten physikalischen Zahlen berechnet, daß durch das Verschwinden einer Kilogrammkalorie 365 Kilogrammmeter Arbeit erzeugt werden können, und umgekehrt. Joule hingegen hat durch eine große Reihe feiner und mannigfaltiger Versuche, die 1843 beginnt, das mechanische Äquivalent der Kilogrammkalorie schließlich viel genauer zu 425 Kilogrammmeter bestimmt.

Schätzt man jede physikalische Zustandsänderung nach der mechanischen Arbeit, welche beim Verschwinden derselben geleistet werden kann, und nennt dieses Maß Energie, so kann man alle physikalischen Zustandsänderungen, so verschiedenartig dieselben sein mögen, mit demselben gemeinsamen Maß messen und sagen: Die Summe aller Energien bleibt konstant. Dies ist die Form, welche das Prinzip vom ausgeschlossenen perpetuum mobile bei seiner Erweiterung über die ganze Physik durch Mayer, Joule, Helmholtz und W. Thomson (Lord Kelvin) angenommen hat.

Nachdem nachgewiesen war, daß Wärme verschwinden muß, wenn auf Kosten derselben mechanische Arbeit geleistet werden soll, konnte der Carnotsche Satz nicht mehr als ein vollständiger Ausdruck der Tatsachen angesehen werden. Die Vervollständigung desselben hat zuerst Clausius (1850) – Thomson folgte 1851 nach – angegeben. Dieselbe lautet: Wenn eine Wärmemenge Q' bei einem umkehrbaren Prozeß in Arbeit verwandelt wird, so sinkt eine andere Wärmemenge Q von der absoluten Darunter versteht man die Celsiustemperatur von 273 unter dem Eispunkt gerechnet. Temperatur T ₁ auf die absolute Temperatur T ₂. Hierbei hängt Q' nur von Q, T ₁, T ₂ ab, ist dagegen von den angewendeten Stoffen und von der Art des Prozesses (sofern derselbe überhaupt verlustlos) unabhängig. Infolge des letzteren Umstandes genügt es, die Beziehung für einen physikalisch wohlbekannten Stoff (z. B. ein Gas) und einen bestimmten beliebig einfachen Prozeß zu bestimmen. Dieselbe ist zugleich die allgemein giltige. Auf diesem Wege findet man

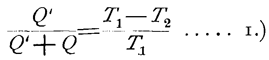
d. h. der Quotient aus der in Arbeit verwandelten (nutzbaren) Wärme Q' und der Summe der verwandelten und übergeführten (der gesamten verbrauchten) Wärme, der sogenannte ökonomische Koëffizient des Prozesses ist:

4. Die Vorstellungen über die Wärme.

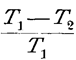
Wenn ein kalter Körper mit einem warmen Körper in Berührung kommt, bemerkt man, daß der erstere sich erwärmt, der letztere sich abkühlt. Man kann sagen, daß der eine Körper auf Kosten des andern sich erwärmt. Dies legt die Vorstellung von einem Etwas, von einem Wärmestoff nahe, welcher aus dem einen Körper in den andern übergeht. Kommen zwei Wassermassen m und m' von ungleicher Temperatur mit einander in Berührung, so zeigt es sich, daß bei raschem Temperaturausgleich deren gegenseitige Temperaturänderungen u und u' den Massen umgekehrt proportioniert, und von entgegengesetztem Zeichen sind, so daß die algebraische Summe der Produkte ist

Black hat die für die Beurteilung des Vorganges maßgebenden Produkte m u, m' u' Wärmemengen genannt. Man kann sich dieselben mit Black sehr anschaulich als Maße von Stoffmengen vorstellen. Wesentlich ist aber nicht dieses Bild, sondern wesentlich ist die Unveränderlichkeit jener Produktensummen bei bloßen Leitungsvorgängen. Wenn irgendwo eine Wärmemenge verschwindet, erscheint anderswo dafür eine gleich große. Das Festhalten dieser Vorstellung führt zur Entdeckung der spezifischen Wärme. Schließlich erkennt Black, daß für eine verschwundene Wärmemenge auch etwas anderes, nämlich Schmelzung oder Verdampfung einer gewissen Stoffmenge erscheinen kann. Er hält die liebgewordene Vorstellung hier mit einer gewissen Freiheit noch fest, und betrachtet die verschwundene Wärmemenge als noch vorhanden, aber als latent.

Die allgemein geläufige Vorstellung vom Wärmestoff wurde durch die Arbeiten von Mayer und Joule mächtig erschüttert. Wenn die Wärmemenge vermehrt und vermindert werden kann, sagte man, kann die Wärme kein Stoff, sondern sie muß Bewegung sein. Dieser nebensächliche Satz ist viel populärer geworden als die ganze übrige Energielehre. Wir können uns jedoch überzeugen, daß die Bewegungsvorstellung der Wärme gegenwärtig so unwesentlich ist, als es vorher die Stoffvorstellung war.

Die beiden Vorstellungen sind lediglich durch zufällige historische Umstände gefördert oder gehemmt worden. Daraus, daß der Wärmemenge ein mechanisches Äquivalent entspricht, folgt noch nicht, daß die Wärme kein Stoff ist.

Dies wollen wir uns durch folgende Frage, die aufgeweckte Anfänger zuweilen an mich gerichtet haben, deutlich machen. Gibt es ein mechanisches Äquivalent der Elektrizität, so wie es ein mechanisches Äquivalent der Wärme gibt? Ja und nein! Es gibt kein mechanisches Äquivalent der Elektrizitätsmenge, wie es ein Äquivalent der Wärmemenge gibt, weil dieselbe Elektrizitätsmenge einen sehr verschiedenen Arbeitswert hat, je nach den Umständen, unter welchen sie erscheint; es gibt aber ein mechanisches Äquivalent der elektrischen Energie.

Fügen wir noch eine Frage hinzu. Gibt es ein mechanisches Äquivalent des Wassers? Ein Äquivalent der Wassermenge nicht, wohl aber des Wassergewichtes × Fallhöhe desselben.

Wenn eine Leydnerflasche entladen wird und dabei Arbeit leistet, so stellen wir uns nicht vor, daß die Elektrizitätsmenge verschwindet, indem sie Arbeit leistet, wir nehmen vielmehr an, daß die Elektrizitäten nur in eine andere Lage kommen, indem sich gleiche Quantitäten positiver und negativer mit einander vereinigen.

Woher kommt nun diese Verschiedenheit unserer Vorstellung bei der Wärme und bei der Elektrizität? Sie hat lediglich historische Gründe, ist vollständig konventionell, ja was noch mehr besagt, vollständig gleichgültig. Es sei mir erlaubt, dies zu begründen.

Coulomb konstruierte 1785 seine Drehwage, durch welche er in den Stand gesetzt wurde, die Abstoßung elektrisierter Körper zu messen. Gesetzt, wir hätten zwei kleine Kugeln A und B, welche durchaus gleichförmig elektrisch sind. Diese werden bei einer bestimmten Entfernung r ihrer Mittelpunkte eine gewisse Abstoßung p aufeinander ausüben. Wir bringen nun mit B einen Körper C in Berührung, lassen beide gleichförmig elektrisch werden und messen dann die Abstoßung von B gegen A und von C gegen A bei derselben Distanz r. Die Summe dieser Abstoßungen wird nun wieder p sein. Es ist also etwas bei dieser Teilung konstant geblieben, die Abstoßung. Schreiben wir nun diese Wirkung einem Agens, einem Stoff zu, so schließen wir ungezwungen auf die Konstanz desselben.

Riess konstruierte 1838 sein elektrisches Luftthermometer. Dasselbe gibt ein Maß für die durch eine Flaschenentladung produzierte Wärmemenge. Diese Wärmemenge ist nicht der nach Coulombschem Maß in der Flasche enthaltenen Elektrizitätsmenge proportional, sondern wenn q diese Menge und s ein von der Oberfläche, Form und Glasdicke der Flasche abhängiger Faktor ist, proportional q ²/s, oder kurz proportional der Energie der geladenen Flasche. Wenn wir nun eine Flasche einmal vollständig durch das Thermometer entladen, so erhalten wir eine gewisse Wärmemenge W. Entladen wir aber durch das Thermometer in eine andere Flasche, so erhalten wir weniger als W. Den Rest können wir aber noch erhalten, wenn wir nun beide Flaschen vollständig durch das Luftthermometer entladen, und er wird wieder proportional sein der Energie dieser beiden Flaschen. Bei der ersten unvollständigen Entladung ist also ein Teil der Wirkungsfähigkeit der Elektrizität verloren gegangen.

Wenn eine Flaschenladung Wärme produziert, so ändert sich ihre Energie und ihr Wert nach dem Riessschen Thermometer nimmt ab. Die Menge nach dem Coulombschen Maße jedoch bleibt unverändert.

Nun stellen wir uns einmal vor, das Riesssche Thermometer wäre früher erfunden worden, als die Coulombsche Drehwage, was uns nicht schwer fallen kann, da ja beide Erfindungen von einander unabhängig sind. Was wäre natürlicher gewesen, als daß man die Menge der in einer Flasche enthaltenen Elektrizität nach der im Thermometer produzierten Wärme geschätzt hätte? Dann würde aber diese sogenannte Elektrizitätsmenge sich vermindern bei Produktion von Wärme oder Arbeitsleistung, während sie jetzt unverändert bleibt; dann würde also die Elektrizität kein Stoff, sondern Bewegung sein, während sie jetzt noch ein Stoff ist. Es hat also bloß einen historischen und ganz zufälligen konventionellen Grund, wenn wir über die Elektrizität anders denken als über die Wärme.

So ist es auch mit andern physikalischen Dingen. Das Wasser verschwindet nicht bei Arbeitsleistungen. Warum? Weil wir die Menge des Wassers mit der Wage messen, ähnlich wie die Elektrizität. Denken wir aber, der Arbeitswert des Wassers würde Menge genannt, und müßte also, etwa mit der Mühle, statt mit der Wage gemessen werden, so würde diese Menge in dem Maße verschwinden, als sie Arbeit leistet. – Nun wird man sich leicht vorstellen können, daß mancher Stoff nicht so leicht greifbar wäre wie das Wasser. Wir würden dann die eine Art der Messung mit der Wage gar nicht ausführen können, während uns manche andere Meßweisen unbenommen blieben. Bei der Wärme ist nun das historisch festgesetzte Maß der »Menge« zufällig der Arbeitswert der Wärme. Daher verschwindet er auch, wenn Arbeit geleistet wird. Daß die Wärme kein Stoff sei, folgt hieraus ebensowenig wie das Gegenteil.

Hätte jemand Lust, sich auch heute noch die Wärme als Stoff zu denken, so könnte man ihm dieses Vergnügen immerhin gestatten. Er brauchte ja nur zu denken, daß dasjenige, was wir Wärmemenge nennen, die Energie eines Stoffes sei, dessen Menge unverändert bleibt, während die Energie sich ändert. In der Tat würden wir nach der Analogie der übrigen physikalischen Bezeichnungen viel besser Wärmeenergie anstatt Wärmemenge sagen.

Wenn wir also die Entdeckung anstaunen, daß Wärme Bewegung sei, so staunen wir etwas an, was nie entdeckt worden ist. Es ist vollständig gleichgiltig und hat nicht den geringsten wissenschaftlichen Wert, ob wir uns die Wärme als einen Stoff denken oder nicht.

Die Wärme verhält sich eben in manchen Beziehungen wie ein Stoff, in andern wieder nicht. Die Wärme ist im Dampf so latent, wie der Sauerstoff im Wasser.

5. Die Konformität im Verhalten der Energien.

Die vorausgehenden Betrachtungen gewinnen an Klarheit durch Beachtung der Konformität im Verhalten aller Energien, auf welche ich vor langer Zeit aufmerksam gemacht habe. Ich habe zuerst hierauf hingewiesen in meiner Schrift »Über die Erhaltung der Arbeit« Prag 1872 – Auf die Analogie von mechanischer und thermischer Energie hatte schon vorher Zeuner aufmerksam gemacht. – Weitere Ausführungen habe ich gegeben in: Geschichte und Kritik des Carnotschen Wärmegesetzes. Sitzungsberichte der Wiener Akademie. Dezember 1892.– Man vergl. auch die Ausführungen der modernen »Energetiker«: Helm, Ostwald u. A. Ein Gewicht P auf einer Höhe H ₁ stellt eine Energie W ₁ = PH ₁ vor. Lassen wir dasselbe auf die kleinere Höhe H ₂ sinken, wobei Arbeit geleistet und diese zur Erzeugung von lebendiger Kraft, Wärme, elektrischer Ladung u. s. w. verwendet, kurz umgewandelt wird, so ist noch die Energie W ₂ = PH ₂ übrig. Es besteht nun die Gleichung

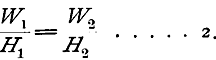
Oder wenn man die umgewandelte Energie mit W' = W ₁ – W ₂, die auf das niedere Niveau übergeführte mit W = W ₂ bezeichnet

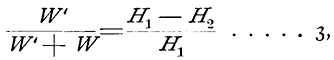
eine Gleichung, welche I (auf S. 196) ganz analog ist. Die betreffende Eigenschaft ist also durchaus nicht der Wärme eigentümlich. Die Gleichung 2 gibt die Beziehung der dem höheren Niveau entnommenen, und der an das tiefere Niveau abgegebenen (zurückbleibenden) Energie; sie besagt, daß diese Energien den Niveauhöhen proportional sind. Eine der Gleichung 2 analoge läßt sich für jede Energieform aufstellen, und demnach läßt sich auch die der Gleichung 3, beziehungsweise 1 entsprechende für jede Form als gültig ansehen. Für die Elektrizität z. B. bedeuten H ₁, H ₂ die Potentiale.

Wenn man zum erstenmal die hier dargelegte Übereinstimmung in dem Umwandlungsgesetz der Energien bemerkt, so erscheint dieselbe überraschend und unerwartet, da man den Grund derselben nicht sofort sieht. Demjenigen aber, der das vergleichend-historische Verfahren befolgt, kann dieser Grund nicht lange verborgen bleiben.

Die mechanische Arbeit ist seit Galilei, wenngleich lange ohne den jetzt gebräuchlichen Namen, ein Grundbegriff der Mechanik und ein wichtiger Begriff der Technik. Die gegenseitige Umwandlung von Arbeit in lebendige Kraft, und umgekehrt, legt die Energieauffassung nahe, welche Huygens zuerst in ausgiebiger Weise verwendet, obgleich erst Th. Young den Namen Energie gebraucht. Nimmt man die Unveränderlichkeit des Gewichtes (eigentlich der Masse) hinzu, so liegt es in Bezug auf die mechanische Energie schon in der Definition, daß die Arbeitsfähigkeit oder (potentielle) Energie eines Gewichtes proportional der Niveauhöhe (im geometrischen Sinne) ist, und daß dieselbe beim Sinken, bei der Umwandlung, proportional der Niveauhöhe abnimmt. Das Nullniveau ist hierbei ganz willkürlich. Hiermit ist also die Gleichung 2, aus welcher die übrigen Formen folgen, gegeben.

Bedenkt man den großen Vorsprung der Entwicklung, den die Mechanik vor den übrigen Gebieten der Physik hatte, so ist es nicht wunderbar, daß man die Begriffe der ersteren überall, wo es anging, anzuwenden suchte. So wurde z. B. der Begriff der Masse in dem Begriff der Elektrizitätsmenge von Coulomb nachgebildet. Bei weiterer Entwicklung der Elektrizitätslehre wurde ebenso in der Potentialtheorie der Arbeitsbegriff sofort angewendet, und es wurde die elektrische Niveauhöhe durch die Arbeit der auf dieselbe gebrachten Mengeneinheit gemessen. Damit ist nun auch für die elektrische Energie ebenfalls die obige Gleichung mit allen Konsequenzen gegeben. Ähnlich ging es mit den anderen Energien.

Als besonderer Fall erscheint jedoch die Wärmeenergie. Daß die Wärme eine Energie ist, konnte nur durch die eigenartigen besprochenen Erfahrungen gefunden werden. Das Maß dieser Energie durch die Blacksche Wärme menge hängt aber an zufälligen Umständen. Zunächst bedingt die zufällige geringe Veränderlichkeit der Wärmekapazität c mit der Temperatur und die zufällige geringe Abweichung der gebräuchlichen Thermometerskalen von der Gasspannungsskala, daß der Begriff Wärmemenge aufgestellt werden kann, und daß die einer Temperaturdifferenz t entsprechende Wärme menge ct der Wärme energie wirklich nahezu proportional ist. Es ist ein ganz zufälliger historischer Umstand, daß Amontons auf den Einfall kam, die Temperatur durch die Gasspannung zu messen. An die Arbeit der Wärme dachte er hierbei gewiß nicht. Mit Bewußtsein ist die Überstimmung zwischen Temperatur und Arbeitsniveau erst durch W. Thomson (1848, 1851) hergestellt worden. Hierdurch werden aber die Temperaturzahlen den Gasspannungen, also den Gasarbeiten, bei sonst gleichen Volumänderungen, proportional. So kommt es, daß die Temperaturhöhen und die Arbeitsniveauhöhen einander wieder proportioniert sind.

Wären von den Gasspannungen stark abweichende Merkmale des Wärmezustandes gewählt worden, so hätte dies Verhältnis sehr kompliziert ausfallen können, und die eingangs betrachtete Übereinstimmung zwischen der Wärme und den andern Energien würde nicht bestehen. Es ist sehr lehrreich, dies zu überlegen.

So liegt also in der Konformität des Verhaltens der Energien kein Naturgesetb, sondern dieselbe ist vielmehr durch die Gleichförmigkeit unserer Auffassung bedingt, und teilweise auch Glücksache.

6. Die Unterschiede der Energien und die Grenzen des Energieprinzipes.

Von jeder Wärmemenge Q, welche bei einem umkehrbaren (verlustlosen) Prozeß zwischen den absoluten Temperaturen T ₁, T ₂ Arbeit leistet, wird nur der Bruchteil in Arbeit verwandelt, während der Rest auf das niedere Temperaturniveau T ₂ übergeführt wird. Dieser übergeführte Teil kann mit dem Aufwand der geleisteten Arbeit durch Umkehrung des Prozesses wieder auf das Niveau T ₁ hinaufgeschafft werden. Ist jedoch der Prozeß nicht umkehrbar, so fließt mehr Wärme als im vorigen Fall auf das niedere Niveau über, und der Mehrbetrag kann nicht mehr ohne einen besonderen Aufwand auf T ₂ geschafft werden. W. Thomson hat deshalb darauf aufmerksam gemacht, daß bei allen nicht umkehrbaren, also bei allen wirklichen Wärmeprozessen Wärmemengen für die mechanische Arbeit verloren gehen, daß also eine Zerstreuung oder Verwüstung von mechanischer Energie stattfindet. Wärme wird immer nur teilweise in Arbeit, Arbeit aber oft ganz in Wärme umgewandelt. Es besteht also eine Tendenb zur Verminderung der mechanischen Energie und zur Vermehrung der Wärmeenergie in der Welt.

Für einen einfachen verlustlosen geschlossenen Kreisprozeß, bei welchem die Wärmemenge Q ₁ dem Niveau T ₁ entzogen und dem Niveau T ₂ die Menge Q ₂, abgegeben wird, besteht entsprechend der Gleichung 2 die Beziehung.

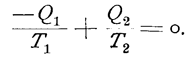
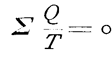
Für beliebig zusammengesetzte umkehrbare Kreisprozesse findet Clausius analog die algebraische Summe, Formel

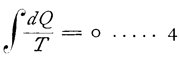
Hierbei werden die einem Niveau entzogenen Wärmemengenelemente negativ, die mitgeteilten positiv gerechnet. Ist der Prozeß nicht umkehrbar, so wächst bei demselben der Ausdruck 4, welchen Clausius Entropie nennt. In Wirklichkeit ist dies immer der Fall, und Clausius sieht sich zu dem Ausspruch gedrängt:

Hat man die Konformität im Verhalten verschiedener Energien erkannt, so muß die hier erwähnte Eigenheit der Wärmeenergie auffallen. Woher kommt dieselbe, da doch jede Energie im allgemeinen nur teilweise in eine andere Form übergeht, gerade so wie die Wärmeenergie? Die Aufklärung liegt in folgendem:

Jede Umwandlung einer Energieart A ist an einen Potentialfall dieser Energieart gebunden, auch für die Wärme. Während aber für die andern Energiearten mit dem Potentialfall auch umgekehrt eine Umwandlung und daher ein Verlust an Energie der im Potential sinkenden Energieart verbunden ist, verhält sich die Wärme anders. Die Wärme kann einen Potentialfall erleiden, ohne – wenigstens nach der üblichen Schätzung – einen Energieverlust zu erfahren. Sinkt ein Gewicht, so muß es notwendig kinetische Energie, oder Wärme oder eine andere Energie erzeugen. Auch eine elektrische Ladung kann einen Potentialfall nicht ohne Energieverlust, d. h. ohne Umwandlung erfahren. Die Warme hingegen kann mit Temperaturfall auf einen Körper von größerer Kapazität übergehen und dieselbe Wärmeenergie bleiben, so lange man nämlich jede Wärme menge als Energie betrachtet. Das ist es, was der Wärme neben ihrer Energieeigenschaft in vielen Fällen den Charakter eines (materiellen) Stoffes, einer Menge gibt.

Betrachtet man die Sache unbefangen, so muß man sich fragen, ob es überhaupt einen wissenschaftlichen Sinn und Zweck hat, eine Wärmemenge, die man nicht mehr in mechanische Arbeit verwandeln kann (z. B. die Wärme eines abgeschlossenen durchaus gleichmäßig temperierten Körpersystems), noch als eine Energie anzusehen. Sicherlich spielt in diesem Fall das Energieprinzip eine ganz müßige Rolle, die ihm nur durch die Gewohnheit zugeteilt wird. Trotz der Anerkennung der Zerstreuung oder Verwüstung der mechanischen Energie, trotz der Entropievermehrung das Energieprinzip aufrecht halten, heißt also ungefähr sich dieselbe Freiheit erlauben, die Black sich gestattet hat, indem er die Schmelzwärme als noch vorhanden, aber als latent ansah.

Es sei noch gestattet zu bemerken, daß die Ausdrücke »Energie der Welt« und »Entropie der Welt« etwas von Scholastik an sich haben. Energie und Entropie sind Maßbegriffe. Welchen Sinn kann es haben, diese Begriffe auf einen Fall anzuwenden, auf welchen dieselben eben nicht anwendbar, in welchem deren Werte unbestimmbar sind?

Könnte man die Entropie der Welt wirklich bestimmen, so würde dieselbe das eigentliche absolute Zeitmaß vorstellen. Es wird so am besten ersichtlich, daß es nur eine Tautologie ist, wenn man sagt: Die Entropie der Welt wächst mit der Zeit. Daß gewisse Veränderungen nur in einem bestimmten Sinne stattfinden, und die Tatsache der Zeit, fällt eben in Eins zusammen.

7. Die Quellen des Energieprinzipes.

Wir sind nun vorbereitet, um die Frage nach den Quellen des Energieprinzips zu beantworten. Alle Naturerkenntnis stammt in letzter Linie aus der Erfahrung. In diesem Sinne haben also diejenigen Recht, welche auch das Energieprinzip als ein Ergebnis der Erfahrung ansehen.

Die Erfahrung lehrt, daß die sinnlichen Elemente α, β, γ, δ ...., in welche die Welt zerlegt werden kann, der Veränderung unterworfen sind, und sie lehrt ferner, daß gewisse dieser Elemente an andere Elemente gebunden sind, so daß sie miteinander auftreten und verschwinden, oder daß das Auftreten der Elemente der einen Art an das Verschwinden der Elemente der andern Art geknüpft ist. Wir wollen hier die Begriffe Ursache und Wirkung ihrer Verschwommenheit und Vieldeutigkeit wegen vermeiden. Das Ergebnis der Erfahrung läßt sich so ausdrücken, daß man sagt: Die sinnlichen Elemente der Welt ( α, β, γ, δ ....) erweisen sich als abhängig von einander. Man denkt sich diese gegenseitige Abhängigkeit am besten so, wie man sich in der Geometrie etwa die gegenseitige Abhängigkeit der Seiten und Winkel eines Dreieckes vorstellt, nur weitaus mannigfaltiger und komplizierter.

Als Beispiel mag eine Gasmasse dienen, welche in einem Cylinder ein bestimmtes Volum ( α) einnimmt, das wir durch Druck ( β) auf den Stempel ändern, während wir den Cylinder mit der Hand befühlen und eine Wärmeempfindung ( γ) erhalten. Vergrößerung des Druckes verkleinert das Volum und steigert die Wärmeempfindung.

Die verschiedenen Tatsachen der Erfahrung gleichen sich nicht vollständig. Die gemeinsamen sinnlichen Elemente derselben treten durch einen Abstraktionsprozeß hervor und prägen sich der Erinnerung ein. Dadurch kommt es zum Ausdruck des Übereinstimmenden ganzer Gruppen von Tatsachen. Schon der einfachste Satz, den wir aussprechen können, ist dem Wesen der Sprache gemäß eine solche Abstraktion. Aber auch den Unterschieden verwandter Tatsachen muß Rechnung getragen werden. Tatsachen können sich so nahe stehen, daß sie dieselbe Art der α, β, γ ... enthalten, und daß sich das α, β, γ der einen von jener der andern nur durch die Zahl der gleichen Teile unterscheidet, in die es zerlegt werden kann. Gelingt es dann Ableitungsregeln der Maßzahlen der α, β, γ .... auseinander anzugeben, so hat man den allgemeinsten und zugleich den allen Unterschieden einer Gruppe von Tatsachen entsprechenden Ausdruck. Dies ist das Ziel der quantitativen Untersuchung.

Ist dieses Ziel erreicht, so hat man gefunden, daß zwischen den α, β, γ .... einer Gruppe von Tatsachen, beziehungsweise zwischen deren Maßzahlen eine Anzahl Gleichungen besteht. Die Tatsache der Veränderung bringt es mit sich, daß die Zahl dieser Gleichungen geringer sein muß als die Zahl der α, β, γ .... Ist erstere um Eins kleiner als letztere, so ist ein Teil der α, β, γ .... durch den andern eindeutig bestimmt.

Das Aufsuchen von Beziehungen der letzteren Art ist das wichtigste Ergebnis der experimentellen Spezialforschung, weil wir dadurch in den Stand gesetzt werden, teilweise gegebene Tatsachen in Gedanken zu ergänzen. Es ist selbstverständlich, daß nur die Erfahrung darüber Aufschluß geben kann, daß zwischen den α, β, γ .... überhaupt Beziehungen bestehen und welcher Art dieselben sind.

Ferner kann nur die Erfahrung lehren, daß solche Beziehungen zwischen den α, β, γ .... bestehen, daß eingetretene Änderungen derselben wieder rückgängig werden können. Ohne diesen Umstand würde, wie leicht ersichtlich, jeder Anlaß zur Aufstellung des Energieprinzipes wegfallen. In der Erfahrung liegt also die letzte Quelle aller Naturerkenntnis und somit in diesem Sinne auch jene des Energieprinzipes.

Dies schließt aber nicht aus, daß das Energieprinzip auch eine logische Wurzel hat, wie sich dies sogleich zeigen wird. Nehmen wir auf Grund der Erfahrung an, eine Gruppe von sinnlichen Elementen α, β, γ .... bestimme eindeutig eine andere Gruppe λ, μ, ν .... Die Erfahrung lehre ferner, daß Änderungen von α, β, γ .... wieder rückgängig werden können. Dann ist es eine logische Folge hiervon, daß jedesmal, wenn α, β, γ .... dieselben Werte annimmt, dies auch bei λ, μ, ν .... der Fall ist, oder, daß bloß periodische Änderungen von α, β, γ .... keine bleibende Änderung von λ, μ, ν .... zur Folge haben können. Ist die Gruppe λ, μ, ν .... eine mechanische, so ist hiermit das perpetuum mobile ausgeschlossen.

Man wird sagen, das sei nur ein Zirkelschluß, und dies sei ohne weiteres zugegeben. Allein psychologisch ist die Situation doch eine wesentlich andere, ob ich nur an die eindeutige Bestimmtheit und Umkehrbarkeit der Vorgänge denke, oder ob ich das perpetuum mobile ausschließe. Die Aufmerksamkeit hat in beiden Fällen eine verschiedene Richtung und verbreitet Licht über verschiedene Seiten der Sache, die allerdings logisch notwendig zusammenhängen.

Sicherlich hat das feste logische Gefüge der Gedanken der großen Forscher ( Stevin, Galilei), welches bewußt oder instinktiv durch das feine Gefühl für die leisesten Widersprüche getragen wird, keinen andern Zweck, als den Gedanken sozusagen einen Grad der Freiheit und damit eine Möglichkeit des Irrtums zu benehmen. Hiermit ist also die logische Wurzel des Satzes vom ausgeschlossenen perpetuum mobile angegeben, d. i. jene allgemeine Überzeugung, welche selbst vor dem Ausbau der Mechanik bestand und bei demselben mitwirkte.

Es ist eine natürliche Sache, daß das Prinzip des ausgeschlossenen perpetuum mobile zuerst auf dem einfacheren Gebiet der reinen Mechanik zur Anerkennung gelangt ist. Zur Übertragung desselben auf das Gesamtgebiet der Physik hat allerdings die Vorstellung beigetragen, daß alle physikalischen Erscheinungen eigentlich mechanische Vorgänge seien. Die obige Entwickelung zeigt aber, wie wenig wesentlich diese Vorstellung ist. Es kommt vielmehr auf die Erkenntnis des allgemeinen Naturzusammenhanges an. Ist dieser festgestellt, so sieht man (mit Carnot), daß es nicht von Belang ist, ob die mechanischen Gesetze unmittelbar oder auf einem Umwege durchbrochen werden.

Das Prinzip des ausgeschlossenen perpetuum mobile steht dem modernen Energieprinzip zwar sehr nahe, es ist mit demselben aber nicht identisch, denn letzteres ergibt sich aus ersterem nur durch eine besondere formale Auffassung. Das perpetuum mobile kann man nach obiger Darlegung ausschließen, ohne den Begriff Arbeit anzuwenden oder auch nur zu kennen. Das moderne Energieprinzip ergibt sich erst durch eine substanzielle Auffassung der Arbeit und jeder physikalischen Zustandsänderung, welche, indem sie rückgängig wird, Arbeit erzeugt. Das starke Bedürfnis nach einer solchen Auffassung, welche durchaus nicht notwendig, aber formal sehr bequem und anschaulich ist, tritt bei J. R. Mayer und Joule hervor. Es wurde schon bemerkt, daß beiden Forschern diese Auffassung sehr nahe gelegt wurde durch die Bemerkung, daß sowohl die Wärmeerzeugung als die mechanische Arbeitsleistung an einen Stoffaufwand gebunden ist. Mayer sagt: »Ex nihilo nil fit«, und an einer andern Stelle: Die Erschaffung oder Vernichtung einer Kraft (Arbeit) liegt außer dem Bereich menschlichen Wirkens. Bei Joule finden wir die Stelle: »It is manifestly absurd to suppose that the powers with which God has endowed matter can be destroyed.« Man hat in solchen Sätzen den Versuch einer metaphysischen Begründung der Energielehre sehen wollen. Ich sehe in denselben lediglich das formale Bedürfnis nach einer anschaulichen, übersichtlichen, einfachen Rechnung, welches sich im praktischen Leben entwickelt hat, und das man nun, so gut es geht, auf das Gebiet der Wissenschaft überträgt. In der Tat schreibt Mayer an Griesinger: »Fragst Du mich endlich, wie ich auf den ganzen Handel gekommen, so ist die einfache Antwort die: auf meiner Seereise mit dem Studium der Physiologie mich fast ausschließlich beschäftigend, fand ich die neue Lehre aus dem zureichenden Grunde, weil ich das Bedürfnis derselben lebhaft erkannte.« ...

Die substanzielle Auffassung der Arbeit (Energie) ist keineswegs eine notwendige, und es fehlt auch viel daran, daß mit dem Bedürfnis nach einer solchen Auffassung auch schon die Aufgabe gelöst wäre. Vielmehr sehen wir, wie Mayer sich bemüht, nach und nach seinem Bedürfnis zu entsprechen. Er hält zuerst die Bewegungsquantität ( m v) für äquivalent der Arbeit, und verfällt erst später auf die lebendige Kraft. Im Gebiete der Elektrizität vermag er den der Arbeit äquivalenten Ausdruck nicht anzugeben; dies geschieht erst später durch Helmholtz. Das formale Bedürfnis ist also zuerst vorhanden, und die Naturauffassung wird demselben erst allmählich angepaßt.

Die Bloßlegung der experimentellen, logischen und formalen Wurzel des heutigen Energieprinzipes dürfte wesentlich zur Beseitigung der Mystik beitragen, welche diesem Prinzip noch anhaftet. In Bezug auf unser formales Bedürfnis nach der einfachsten anschaulichsten substanziellen Auffassung der Vorgänge in unserer Umgebung bleibt es eine offene Frage, wie weit die Natur demselben entspricht, oder wie weit wir demselben entsprechen können. Nach einer der obigen Ausführungen scheint es, daß die Substanzauffassung des Energieprinzipes ebenso wie die Blacksche Substanzauffassung der Wärme ihre natürlichen Grenzen in den Tatsachen hat, über welche hinaus sie nur künstlich festgehalten werden kann.

Inhalt

XII. Über das Prinzip der Erhaltung der Energie.