
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Vortrag, gehalten auf der internationalen Elektrizitäts-Ausstellung zu Wien am 4. September 1883.
Es wurde mir die Aufgabe zu teil, vor Ihnen die quantitativen Grundbegriffe der Elektrostatik: »Elektrizitätsmenge«, »Potential«, »Capazität« in allgemein verständlicher Weise zu entwickeln. Es wäre nicht schwierig, selbst in dem Rahmen einer Stunde, die Augen durch zahlreiche schöne Experimente zu beschäftigen, und die Phantasie mit mannigfaltigen Vorstellungen zu erfüllen. Allein von einer klaren und mühelosen Übersicht der Tatsachen wären wir dann noch weit entfernt. Noch würde uns das Mittel fehlen, die Tatsachen in Gedanken genau nachzubilden, was für den Theoretiker und Praktiker von gleicher Wichtigkeit ist. Dieses Mittel sind eben die Maßbegriffe der Elektrizitätslehre.
So lange nur wenige vereinzelte Forscher sich mit einem Gebiete beschäftigen, so lange jeder Versuch noch leicht wiederholt werden kann, genügt wohl eine Fixierung der gesammelten Erfahrungen durch eine oberflächliche Beschreibung. Anders verhält es sich, wenn jeder die Erfahrungen vieler verwerten muß, wie dies der Fall ist, sobald die Wissenschaft eine breite Basis gewonnen hat, und noch mehr, sobald sie anfängt, einem wichtigen Zweige der Technik Nahrung zu geben und umgekehrt aus dem praktischen Leben wieder in großartiger Weise Erfahrungen zu schöpfen. Dann müssen die Tatsachen so beschrieben werden, daß jeder und allerorten dieselben aus wenigen leicht zu beschaffenden Elementen in Gedanken genau zusammensetzen, und nach dieser Beschreibung reproduzieren kann; dies geschieht mit Hilfe der Maßbegriffe und der internationalen Maße.
Die in dieser Richtung in der Periode der rein wissenschaftlichen Entwicklung namentlich durch Coulomb (1784), Gauss (1833) und Weber begonnene Arbeit wurde mächtig gefördert durch die Bedürfnisse der großen technischen Unternehmungen, die sich besonders seit der Legung des ersten transatlantischen Kabels fühlbar machten, und wurde glanzvoll der Vollendung entgegengeführt durch die Arbeiten der British Association (1861) und des Pariser Kongresses (1881), namentlich durch die Bemühungen von Sir William Thomson. (Lord Kelvin.)
Es versteht sich, daß ich Sie in der mir zugemessenen Zeit nicht alle die langen und gewundenen Pfade führen kann, welche die Wissenschaft wirklich eingeschlagen hat, daß es nicht möglich ist, bei jedem Schritt an alle die kleinen Vorsichten zur Vermeidung von Fehltritten zu erinnern, welche die früheren Schritte uns gelehrt haben. Ich muß mich vielmehr mit den einfachsten und rohesten Mitteln behelfen. Die kürzesten Wege von den Tatsachen zu den Begriffen will ich Sie führen, wobei es mir allerdings nicht möglich sein wird, allen den Kreuz- und Quergedanken, die sich beim Anblick der Seitenwege einstellen können, ja einstellen müssen, zuvorzukommen.
Wir betrachten zwei kleine, gleiche, leichte, frei aufgehängte Körperchen (Fig. 30), die wir entweder durch Reibung mit einem dritten Körper oder durch Berührung mit einem schon elektrischen Körper »elektrisieren.« Sofort zeigt sich eine abstoßende Kraft, welche die beiden Körperchen von einander (der Wirkung der Schwere entgegen) entfernt. Diese Kraft vermöchte dieselbe mechanische Arbeit wieder zu leisten, durch deren Aufwendung sie entstanden ist. Würden die beiden Körper ungleichnamig elektrisiert, so würden sie anziehend aufeinander wirken.
Coulomb hat sich nun durch sehr umständliche Versuche mit Hilfe der Drehwage überzeugt, daß, wenn jene Körperchen bei einem Abstande von 2 Cm. z. B. sich etwa mit derselben Kraft abstoßen, mit welcher ein Milligrammgewicht zur Erde zu fallen strebt, daß sie dann bei der Hälfte der Entfernung, bei 1 Cm., mit 4 Milligramm, und bei verdoppeltem Abstande, bei 4 Cm., mit nur ¼ Milligramm sich abstoßen. Er fand, daß die elektrische Kraft verkehrt proportional dem Quadrat der Entfernung wirkt.
Stellen wir uns nun vor, wir hätten ein Mittel, die elektrische Abstoßung durch Gewichte zu messen, welches einfache Mittel z. B. die elektrischen Pendel selbst sind, so können wir folgende Beobachtungen machen.
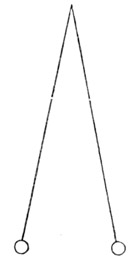
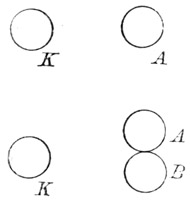
Fig. 30. Fig.31.
Der Körper A (Fig. 31), wird von dem Körper K bei 2 Cm. Entfernung etwa mit 1 Milligramm Druck abgestoßen. Berühren wir nun A mit einem gleichen Körper B, so geht die Hälfte dieser Abstoßungskraft an denselben über. Sowohl A als B werden nun bei 2 Cm. Entfernung von K nur mit je ½ Milligramm, beide zusammen aber wieder mit 1 Milligramm abgestoßen. Die Teilung der elektrischen Kraft unter die sich berührenden Körper ist eine Tatsache. Eine keineswegs notwendige aber nützliche Zutat ist es, wenn wir uns vorstellen, in dem Körper A sei eine elektrische Flüssigkeit vorhanden, an deren Menge die elektrische Kraft gebunden ist, welche zur Hälfte nach B überfließt. Denn an die Stelle der neuen physikalischen Vorstellung tritt hiermit eine uns längst geläufige, welche wie von selbst in den gewohnten Bahnen abläuft.
Entsprechend dieser Vorstellung bezeichnen wir als die Elektrizitätsmenge Eins nach dem sehr allgemein angenommenen Centimeter-Gramme-Sekundensystem (C.-G.-S.) diejenige, welche auf eine gleiche Menge in der Entfernung von 1 Cm., mit der Krafteinheit, d. h. mit einer Kraft abstoßend wirkt, welche der Masse von 1 Gr. in der Sekunde einen Geschwindigkeitszuwachs von 1 Cm. erteilt. Da eine Grammmasse durch die Erdschwere einen Geschwindigkeitszuwachs von etwa 981 Cm. in der Sekunde erhält, so wird sie hiernach mit 981 Cm. (oder rund 1000) Krafteinheiten des Centimeter-Gramme-Sekundensystems angezogen, und ein Milligrammgewicht strebt ungefähr mit einer Krafteinheit dieses Systems zur Erde zu fallen.
Hiernach kann man sich leicht eine anschauliche Vorstellung von der Einheit der Elektrizitätsmenge verschaffen. Zwei je ein Gramm schwere kleine Körperchen K sollen an 5 M. langen, fast gewichtslosen vertikalen Fäden so aufgehängt sein, daß sie sich berühren. Werden beide gleich stark elektrisch, und entfernen sie sich hierbei um 1 Cm. von einander, so entspricht die Ladung eines jeden der elektrostatischen Einheit der Elektrizitätsmenge; denn die Abstoßung hält dann der Schwerkraft-Komponente von rund 1 Milligramm das Gleichgewicht, welche die Körperchen einander zu nähern strebt.
Vertikal unter einem an einer Wage äquilibrierten, sehr kleinen Kügelchen befindet sich ein zweites in 1 Cm. Entfernung. Werden beide gleich elektrisiert, so wird das Kügelchen an der Wage durch die Abstoßung scheinbar leichter. Stellt ein Zuleggewicht von 1 Milligramm das Gleichgewicht her, so enthält jedes Kügelchen rund die elektrostatische Einheit der Elektrizitätsmenge.
Mit Rücksicht darauf, daß dieselben elektrischen Körper in verschiedener Entfernung verschiedene Kräfte aufeinander ausüben, könnte man an dem dargelegten Maß der Menge Anstoß nehmen. Was ist das für eine Menge, die bald mehr, bald weniger wiegt, wenn man so sagen darf? Allein diese scheinbare Abweichung von der gewöhnlichen Mengenbestimmung im bürgerlichen Leben durch das Gewicht ist vielmehr, genau betrachtet, eine Übereinstimmung. Auch eine schwere Masse wird auf einem hohen Berg schwächer zur Erde gezogen als im Meeresniveau, und wir können von einer Bestimmung des Niveaus nur deshalb Umgang nehmen, weil wir den Körper mit dem Gewichtssatz ohnehin immer nur in demselben Niveau vergleichen.
Würden wir aber von den beiden gleichen Gewichten, welche sich an einer Wage das Gleichgewicht halten, das eine dem Erdmittelpunkte merklich nähern, indem wir dasselbe an einem sehr langen Faden aufhängen, wie dies Prof. v. Jolly in München ausgedacht hat, so würden wir diesem letztereren ein entsprechendes Übergewicht verschaffen.
Denken wir uns zwei verschiedene elektrische Flüssigkeiten, die positive und die negative, von derartiger Beschaffenheit, daß die Teile dieser beiden Flüssigkeiten sich gegenseitig verkehrt quadratisch anziehen, jene derselben Flüssigkeit aber nach demselben Gesetz gegenseitig abstoßen, denken wir uns in unelektrischen Körpern beide Flüssigkeiten in gleichen Mengen gleichmäßig verteilt, dagegen in elektrischen Körpern die eine der beiden im Überschuß, denken wir uns ferner in Leitern die Flüssigkeiten frei beweglich, in Nichtleitern unbeweglich, so haben wir die von Coulomb zu mathematischer Schärfe entwickelte Vorstellung. Wir brauchen uns nur dieser Vorstellung hinzugeben, so sehen wir im Geiste die Flüssigkeitsteilchen eines etwa positiv geladenen Leiters, sich möglichst von einander entfernend, alle nach der Oberfläche des Leiters wandern, dort die vorspringenden Teile und Spitzen aufsuchen, bis hierbei die größtmögliche Arbeit geleistet ist. Bei Vergrößerung der Oberfläche sehen wir eine Zerstreuung, bei Verkleinerung derselben eine Verdichtung der Teilchen. In einem zweiten, dem ersteren angenäherten unelektrischen Leiter, sehen wir sofort die beiden Flüssigkeiten sich trennen, die positive auf der abgekehrten, die negative auf der zugekehrten Seite der Oberfläche sich sammeln. Darin, daß diese Vorstellung alle nach und nach durch mühsame Beobachtung gefundenen Tatsachen anschaulich und wie von selbst reproduziert, liegt ihr Vorteil und ihr wissenschaftlicher Wert. Allerdings ist hiermit auch ihr Wert erschöpft, und wir dürften nicht etwa nach den beiden hypothetischen Flüssigkeiten, die wir ja nur hinzugedacht haben, in der Natur suchen, ohne auf Abwege zu geraten. Die Coulombsche Vorstellung kann durch eine gänzlich andere, wie z. B. die Faradaysche, ersetzt werden. Und das Richtigste bleibt es immer, nachdem die Übersicht gewonnen ist, auf das Tatsächliche, auf die elektrischen Kräfte zurückzugehen.
Wir wollen uns nun zunächst mit der Vorstellung der Elektrizitäts menge und der Art, dieselbe bequem zu messen oder zu schätzen, vertraut machen.
Wir denken uns eine gewöhnliche Leydener-Flasche, Fig. 32. deren innere und äußere Belegung mit leitenden, etwa 1 Cm. von einander abstehenden Funkenkugeln verbunden ist. Ladet man die innere Belegung mit der Elektrizitätsmenge + q, so tritt auf der äußeren Belegung durch das Glas hindurch eine Verteilung ein. Eine der Menge + q fast gleiche Die abfließende Menge ist tatsächlich etwas kleiner als q. Sie wäre der Menge q nur dann gleich, wenn die innere Belegung der Flasche von der äußern ganz eingeschlossen wäre. positive Menge fließt in die Erde ab, während die entsprechende - q auf der äußeren Belegung bleibt. Die Funkenkugeln enthalten von diesen Mengen ihren Anteil, und wenn die Menge q eben groß genug ist, tritt eine Durchbrechung der isolierenden Luft zwischen den Kugeln und eine Selbstentladung der Flasche ein. Zur Selbstentladung der Flasche bei bestimmter Distanz und Größe der Funkenkugeln gehört jedesmal die Ladung durch die bestimmte Elektrizitäts-Menge q.
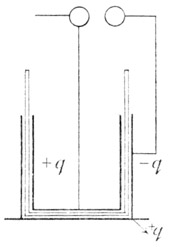
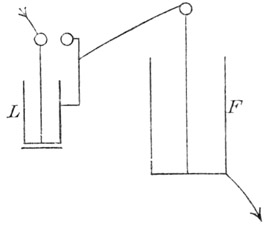
Fig. 32 Fig. 33.
Isolieren wir nun die äußere Belegung der eben beschriebenen Laneschen Maßflasche L, und setzen dieselbe mit der inneren Belegung einer außen abgeleiteten Flasche F in Verbindung (Fig. 33). Jedesmal wenn L mit + q geladen wird, tritt auch + q auf die innere Belegung von F,und eine Selbstentladung der Flasche L, die nun wieder leer ist, findet statt. Die Zahl der Entladungen der Flasche L gibt also ein Maß der Menge, welche in die Flasche F geladen wurde, und wenn man nach 1, 2, 3 ... Selbstentladungen von L die Flasche F entladet, kann man sich von der entsprechenden succesiven Vermehrung ihrer Ladung überzeugen.
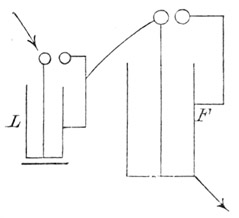
Fig. 34.
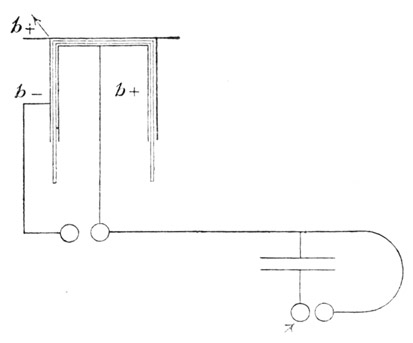
Fig. 35.
Versehen wir die Flasche F mit gleich großen und gleich weit abstehenden Funkenkugeln zur Selbstentladung wie die Flasche L. (Fig. 34.) Finden wir dann z. B., daß Fünf Entladungen der Maßflasche stattfinden, bevor eine Selbstentladung der Flasche F eintritt, so sagt dies, daß die Flasche F bei gleichem Abstand der Funkenkugeln, bei gleicher Schlagweite, die Fünffache Elektrizitätsmenge zu fassen vermag wie L, daß sie die fünffache Kapazität hat.
Fußnote aus technischen Gründen im Text wiedergegeben. Re. Genau ist dies allerdings nicht richtig. Zunächst ist zu bemerken, daß sich die Flasche
L zugleich mit der Maschinenelektrode entladen muß. Die Flasche
F hingegen wird immer zugleich mit der äußeren Belegung der Flasche
L entladen. Nennt man also die Kapazität der Maschinenelektrode
E, die der Maßflasche
L, die Kapazität der äußeren Belegung von
L aber
A, und jene der Hauptflasche
F, so würde dem Beispiel im Text die Gleichung entsprechen:
![]() . Eine weitere Störung der Genauigkeit bringen die Entladungsrückstände mit sich.
. Eine weitere Störung der Genauigkeit bringen die Entladungsrückstände mit sich.
Wir wollen nun die Maßflasche L, mit welcher wir sozusagen in die Flasche F einmessen, durch eine Franklinsche Tafel aus zwei parallelen ebenen Metallplatten ersetzen (Fig. 35), welche nur durch Luft getrennt sind. Genügen nun beispielsweise 30 Selbstentladungen der Tafel, um die Flasche zu füllen, so sind hierzu etwa 10 Entladungen hinreichend, wenn man den Luftraum zwischen den beiden Platten durch einen eingeschobenen Schwefelkuchen ausfüllt. Die Kapazität der Franklinschen Tafel aus Schwefel ist also etwa dreimal größer, als jene eines gleich geformten und gleich großen Luftkondensators oder, wie man sich auszudrücken pflegt, das spezifische Induktionsvermögen des Schwefels (jenes der Luft als Einheit genommen) ist etwa 3. Mit Rücksicht auf die in [vorige] Anmerkung angedeuteten Korrektionen erhielt ich für die Dielektrizitäts-Konstante des Schwefels die Zahl 3.2, welche mit den durch feinere Methoden gewonnenen Zahlen genügend übereinstimmt. Genau genommen müßte man eigentlich die beiden Kondensatorplatten einmal ganz in Luft, das anderemal ganz in Schwefel versenken, wenn das Kapazitäts-Verhältnis der Dielektrizitäts-Konstante entsprechen, sollte. In Wirklichkeit ist aber der Fehler, der dadurch entsteht, daß man nur eine Schwefelplatte einschiebt, welche den Raum zwischen den beiden Platten genau ausfüllt, nicht von Belang. Wir sind hier auf eine sehr einfache Tatsache gestoßen, welche uns die Bedeutung der Zahl, die man Dielektrizitäts-Konstante oder spezifisches Induktionsvermögen nennt, und deren Kenntnis für die Theorie unterseeischer Kabel so wichtig ist, nahe legt.
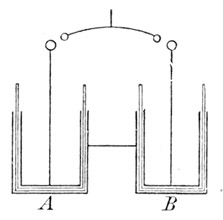
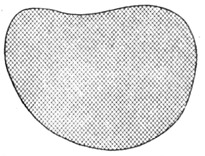
Fig. 36. Fig. 37.
Wir betrachten eine Flasche A, welche mit einer gewissen Elektrizitätsmenge geladen ist. Wir können die Flasche direkt entladen. Wir können aber auch die Flasche A (Fig. 36) teilweise in eine Flasche B entladen, indem wir die gleichnamigen Belegungen mit einander verbinden. Ein Teil der Elektrizitätsmenge geht hierbei unter Funkenbildung in die Flasche B über und wir finden nun beide Flaschen geladen.
Daß die Vorstellung einer unveränderlichen Elektrizitätsmenge als Ausdruck einer reinen Tatsache betrachtet werden kann, sehen wir auf folgende Art. Wir denken uns einen beliebigen elektrischen Leiter, Fig. 37, der isoliert ist, zerschneiden ihn in eine große Anzahl kleiner Stückchen und bringen dieselben mit einer isolierten Zange auf 1 Cm. Entfernung von einem elektrischen Körper, der auf einen gleichen, gleich beschaffenen in derselben Distanz die Krafteinheit ausübt. Die Kräfte, welche der letztere Körper auf die einzelnen Leiterstücke ausübt, zählen wir zusammen. Diese Kraftsumme ist nichts anderes als die Elektrizitätsmenge des ganzen Leiters. Sie bleibt immer dieselbe, ob wir die Form und Größe des Leiters ändern, ob wir ihn einem andern elektrischen Leiter nähern oder entfernen, so lange wir nur den Leiter isoliert lassen, d. h. nicht entladen.
Auch von einer anderen Seite her scheint sich für die Vorstellung der Elektrizitätsmenge eine reelle Basis zu ergeben. Wenn durch eine Säule von angesäuertem Wasser ein Strom, also nach unserer Vorstellung eine bestimmte Elektrizitätsmenge per Sekunde hindurchgeht, so wird mit dem positiven Strom Wasserstoff, gegen den Strom Sauerstoff an den Enden der Säule ausgeschieden. Für eine bestimmte Elektrizitätsmenge erscheint eine bestimmte Sauerstoffmenge. Man kann sich die Wassersäule als eine Wasserstoffsäule und eine Sauerstoffsäule denken, die sich durch einander hindurch schieben, und kann sagen, der elektrische Strom ist ein chemischer Strom und umgekehrt. Wenngleich diese Vorstellung im Gebiete der statischen Elektrizität und bei nicht zersetzbaren Leitern schwerer festzuhalten ist, so ist ihre weitere Entwicklung doch keineswegs aussichtslos.
Die Vorstellung der Elektrizitätsmenge ist also keineswegs eine so luftige, wie es scheinen könnte, sondern dieselbe vermag uns mit Sicherheit durch die Mannigfaltigkeit der Erscheinungen zu leiten, und wird uns durch die Tatsachen in beinahe greifbarer Weise nahegelegt. Wir können die elektrische Kraft in einem Körper aufsammeln, mit einem Körper dem anderen zumessen, aus einem Körper in den anderen überführen, sowie wir Flüssigkeit in einem Gefäß aufsammeln, mit einem Gefäß in ein anderes einmessen, aus einem in das andere übergießen können.
Zur Beurteilung mechanischer Vorgänge hat sich an der Hand der Erfahrung ein Maßbegriff als vorteilhaft erwiesen, der mit dem Namen Arbeit bezeichnet wird. Eine Maschine gerät nur dann in Bewegung, wenn die an derselben wirksamen Kräfte Arbeit leisten können.
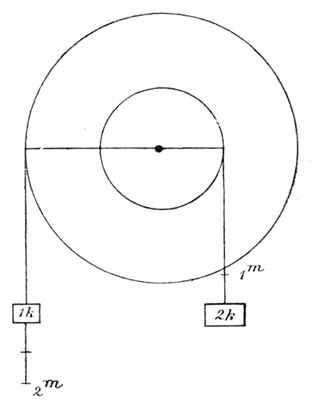
Fig. 38.
Betrachten wir z. B. ein Wellrad (Fig. 38) mit den Halbmessern 1 und 2 M., an welchen beziehungsweise die Gewichte 2 und 1 Kilo angebracht sind. Drehen wir das Wellrad, so sehen wir etwa das Kilogewicht um 2 M. sinken, während das Zweikilogewicht um 1 M. steigt. Es ist auf beiden Seiten das Produkt
Kgr. M. Kgr. M.
1 x 2 = 2 x 1
gleich. So lange dieses Produkt beiderseits gleich ist, bewegt sich das Wellrad nicht von selbst. Wählen wir aber die Belastungen oder die Halbmesser so, daß das Produkt Kilo × Meter bei einer Verschiebung auf der einen Seite einen Überschuß erhält, so wird diese Seite sinken. Das Produkt ist also charakteristisch für den mechanischen Vorgang, und ist eben deshalb mit einem besonderen Namen belegt, Arbeit genannt worden.
Bei allen mechanischen Vorgängen, und da alle physikalischen Vorgänge eine mechanische Seite darbieten, bei allen physikalischen Prozessen, spielt die Arbeit eine maßgebende Rolle. Auch die elektrischen Kräfte bringen nur solche Veränderungen hervor, bei welchen Arbeit geleistet wird. Insofern bei den elektrischen Erscheinungen Kräfte ins Spiel kommen, reichen sie ja, mögen sie sonst was immer sein, ins Gebiet der Mechanik hinein und fügen sich den in diesem Gebiete geltenden Gesetzen. Als Maß der Arbeit betrachtet man also das Produkt aus der Kraft in den Wirkungsweg derselben, und in dem C.-G.-S.-System gilt als Arbeitseinheit die Wirkung einer Kraft, welche einer Grammmasse in der Sekunde einen Geschwindigkeitszuwachs von 1 Cm. erteilt auf 1 Cm. Wegstrecke, also rund etwa die Wirkung eines Milligramm-Gewichtsdruckes auf 1 Cm. Wegstrecke.
Von einem positiv geladenen Körper wird Elektrizität, den Abstoßungskräften folgend und Arbeit leistend, wenn eine leitende Verbindung besteht, zur Erde abfließen. An einen negativ geladenen Körper gibt umgekehrt unter denselben Umständen die Erde positive Elektrizität ab. Die elektrische Arbeit, welche bei der Wechselwirkung eines Körpers mit der Erde möglich ist, charakterisiert den elektrischen Zustand des ersteren. Wir wollen die Arbeit, welche wir auf die Einheit der positiven Elektrizitätsmenge aufwenden, wenn wir dieselbe von der Erde zu dem Körper K hinaufschaffen, das Potential des Körpers K nennen.
Fußnote aus technischen Gründen im Text wiedergegeben. Re. Da diese Definition in ihrer einfachen Form zu Mißverständnissen Anlaß geben kann, werden derselben gewöhnlich noch Erläuterungen hinzugefügt. Es ist nämlich klar, daß man keine Elektrizitätsmenge auf
K hinaufschaffen kann, ohne die Verteilung auf
K und das Potential auf
K zu ändern. Man hat sich demnach die Ladungen an
K festgehalten zu denken und eine so kleine Menge hinaufzuführen, daß durch dieselbe keine merkliche Änderung entsteht. Nimmt man die aufgewendete Arbeit so vielmal als jene kleine Menge in der Einheit aufgeht, so erhält man das Potential. – Kurz und scharf läßt sich das Potential eines Körpers
K in folgender Weise definieren. Wendet man das Arbeitselement
d W auf, um das Element
d Q der positiven Menge von der Erde auf den Leiter zu fördern, so ist das Potential des Leiters
K gegeben durch
![]()
Wir schreiben dem Körper K im C. G.-S.-System das Potential + 1 zu, wenn wir die Arbeitseinheit aufwenden müssen, um die positive elektrostatische Einheit der Elektrizitätsmenge von der Erde zu ihm hinaufzuschaffen, das Potential – 1, wenn wir bei derselben Prozedur die Arbeitseinheit gewinnen, das Potential 0, wenn hierbei keine Arbeit geleistet wird.
Den verschiedenen Teilen desselben im elektrischen Gleichgewicht befindlichen Leiters entspricht dasselbe Potential, denn andernfalls würde die Elektrizität, Arbeit leistend in diesem Leiter sich bewegen und es bestünde noch kein Gleichgewicht. Verschiedene Leiter von gleichem Potential, in leitende Verbindung gebracht, bieten keinen Austausch von Elektrizität dar, ebensowenig als bei sich berührenden Körpern von gleicher Temperatur ein Wärmeaustausch oder bei verbundenen Gefäßen von gleichem Flüssigkeitsdruck ein Flüssigkeitsaustausch stattfindet.
Nur zwischen Leitern verschiedenen Potentials findet ein Austausch der Elektrizität statt, und bei Leitern von gegebener Form und Lage ist eine bestimmte Potentialdifferenz notwendig, damit zwischen denselben ein die isolierende Luft durchbrechender Funke überspringt.
Je zwei verbundene Leiter nehmen sofort dasselbe Potential an, und hiermit ist das Mittel gegeben, das Potential eines Leiters mit Hilfe eines anderen hierzu geeigneten, eines sogenannten Elektrometers, ebenso zu bestimmen, wie man die Temperatur eines Körpers mit dem Thermometer bestimmt. Die auf diese Weise gewonnenen Potentialwerte der Körper erleichtern, wie dies nach dem Besprochenen einleuchtet, ungemein das Urteil über deren elektrisches Verhalten.
Denken wir uns einen positiv geladenen Leiter. Verdoppeln wir alle elektrischen Kräfte, welche derselbe auf einen mit der Einheit geladenen Punkt ausübt, d. h. verdoppeln wir an jeder Stelle die Menge, verdoppeln wir also auch die Gesamtladung, so besteht ersichtlich das Gleichgewicht fort. Führen wir aber nun die positive elektrostatische Einheit dem Leiter zu, so haben wir überall die doppelten Abstoßungskräfte zu überwinden wie zuvor, wir haben die doppelte Arbeit aufzuwenden, das Potential hat sich mit der Ladung des Leiters verdoppelt, Ladung und Potential sind einander proportional. Wir können also die gesamte Menge der Elektrizität eines Leiters mit Q, das Potential desselben mit V bezeichnend, schreiben: Q = CV, wobei also C eine Konstante bedeutet, deren Bedeutung sich ergibt, wenn wir bedenken, daß Q = C/V ist. Dividieren wir aber die Anzahl der Mengeneinheiten eines Leiters durch die Anzahl seiner Potentialeinheiten, so erfahren wir, welche Menge auf die Einheit des Potentials entfällt. Wir nennen nun die betreffende Zahl C die Kapazität des Leiters, und haben somit an Stelle der relativen eine absolute Bestimmung der Kapazität gesetzt. Zwischen den Begriffen »Wärmekapazität« und »elektrische Kapazität« besteht eine gewisse Übereinstimmung, doch darf auch der Unterschied beider Begriffe nicht außer acht gelassen werden. Die Wärmekapazität eines Körpers hängt nur von ihm selbst ab. Die elektrische Kapazität eines Körpers K wird aber durch alle Nachbarkörper beeinflußt, indem auch die Ladung dieser Körper das Potential von K ändern kann. Um demnach dem Begriff Kapazität ( C) des Körpers K einen unzweideutigen Sinn zu geben, versteht man unter C das Verhältnis Q/V für den Körper K bei einer gegebenen Lage aller Nachbarkörper und Ableitung aller benachbarten Leiter zur Erde, In den für die Praxis wichtigen Fällen gestaltet sich die Sache viel einfacher. Die Kapazität einer Flasche z. B., deren innere Belegung durch die äußere abgeleitete fast umschlossen ist, wird durch geladene oder ungeladene Nebenleiter nicht merklich beeinflußt.
In einfachen Fällen läßt sich nun der Zusammenhang zwischen Ladung, Potential und Kapazität ohne Schwierigkeit ermitteln. Der Leiter sei z. B. eine Kugel vom Radius r frei in einem großen Luftraum. Dann verteilt sich die Ladung q, da keine anderen Leiter in der Nähe sind, gleichmäßig auf ihrer Oberfläche, und einfache geometrische Betrachtungen ergeben für das Potential den Ausdruck V = q/r. Hiernach ist also q/V = r, d. h. die Kapazität wird durch den Radius, und zwar im C.-G.-S.-System in Centimetern gemessen. Diese Formeln ergeben sich sehr leicht aus dem Newtonschen Satze, daß eine homogene Kugelschicht, deren Elemente verkehrt quadratisch wirken, auf einen inneren Punkt gar keine Kraft ausübt, auf einen äußeren aber wie die im Kugelmittelpunkt vereinigte Masse wirkt. Aus demselben Satz fließen auch noch die zunächst folgenden Formeln. Eine elementare Ableitung findet sich bei Mach, Leitfaden der Physik. Prag 1891. S. 198. Es ist auch klar, da ein Potential eine Menge durch eine Länge dividiert ist, so muß eine Menge, durch ein Potential dividiert, eine Länge sein.
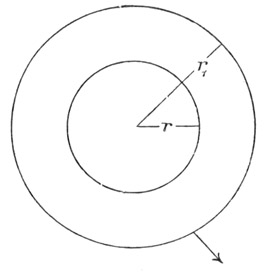
Fig. 39.
Denken wir uns (Fig. 39) eine Flasche aus zwei konzentrischen leitenden Kugelflächen von den Radien
r und r
1 gebildet, welche nur Luft zwischen sich enthalten. Leitet man die äußere Kugel zur Erde ab, und ladet die innere durch einen dünnen durch die erstere isoliert hindurchgeführten Draht mit der Menge
Q, so ist
![]() Q, und die Kapazität in diesem Falle
Q, und die Kapazität in diesem Falle
![]() , also wenn z. B. r = 16, r
1 = 19, nahe = 100 Cm.
, also wenn z. B. r = 16, r
1 = 19, nahe = 100 Cm.
Diese einfachen Fälle wollen wir nun benützen, um das Prinzip der Kapazitätsbestimmung und der Potentialbestimmung zu erläutern. Zunächst ist klar, daß wir die Flasche aus konzentrischen Kugeln von bekannter Kapazität als Maßflasche benutzen, und mit Hilfe derselben in der bereits dargelegten Weise die Kapazität einer vorgelegten Flasche F ermitteln können. Wir finden z. B., daß 37 Entladungen dieser Maßflasche von der Kapazität 100 die vorliegende Flasche zu gleicher Schlagweite, das ist zu gleichem Potential laden. Demnach ist die Kapazität der vorliegenden Flasche 3700 Cm. Die große Batterie des Prager physikalischen Institutes, welche aus 16 solchen nahe gleichen Flaschen besteht, hat demnach eine Kapazität von etwas mehr als 50 000 Cm., also dieselbe Kapazität wie eine frei im Luftraum schwebende Kugel von mehr als 1 Km. Durchmesser. Diese Bemerkung kann uns den großen Vorteil nahe legen, welchen Leydener Flaschen bei Aufspeicherung von Elektrizität gewöhnlichen Konduktoren gegenüber gewähren. In der Tat unterscheiden sich Flaschen von einfachen Konduktoren, wie schon Faraday wußte, wesentlich nur durch die große Kapazität.
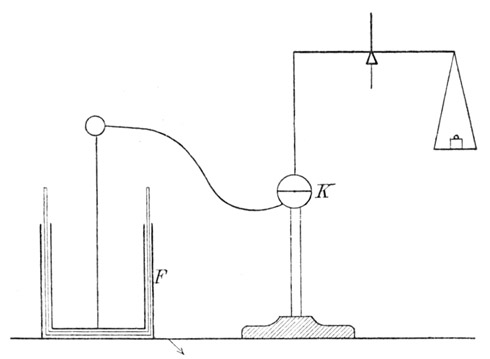
Fig. 40.
Zum Zwecke der Potentialbestimmung denken wir uns die innere Belegung einer Flasche
F, deren äußere Belegung abgeleitet ist, durch einen dünnen langen Draht mit einer leitenden Kugel
K verbunden, welche in einem Luftraume frei aufgestellt ist, gegen dessen Dimensionen der Kugelradius verschwindet. (Fig. 40.) Die Flasche und die Kugel nehmen sofort gleiches Potential an. Auf der Kugeloberfläche aber befindet sich, wenn dieselbe von allen anderen Leitern weit genug entfernt ist, eine gleichmäßige Schicht von Elektrizität. Enthält die Kugel vom Radius r die Ladung
q, so ist
Q = v/r ihr Potential. Ist nun die obere Kugelhälfte abgeschnitten und an einer Wage, an deren Balken sie mit Seidenfäden befestigt ist, äquilibriert, so wird die obere Hälfte von der unteren mit der Kraft
![]() abgestoßen. Diese Abstoßung P kann durch ein Zuleggewicht ausgeglichen und folglich bestimmt werden. Das Potential ist dann V - √8P.
abgestoßen. Diese Abstoßung P kann durch ein Zuleggewicht ausgeglichen und folglich bestimmt werden. Das Potential ist dann V - √8P.
Daß das Potential der Wurzel aus der Kraft proportional geht, ist leicht einzusehen. Bei doppeltem oder dreifachem Potential ist die Ladung aller Teile verdoppelt oder verdreifacht, demnach ihre gegenseitige Abstoßungswirkung schon vervierfacht, verneunfacht.
Betrachten wir ein besonderes Beispiel. Ich will auf der Kugel das Potential 40 herstellen. Welches Übergewicht muß ich der Kugelhälfte in Grammen geben, damit der Abstoßungskraft eben das Gleichgewicht gehalten wird? Da ein Grammgewicht etwa 1000 Krafteinheiten entspricht, so haben wir folgende einfache Rechnung 40 x 40 = 8 x 1000 · x, wobei x die Anzahl der Gramme bedeutet. Es ist rund x = 0·2 Gramme. Ich lade die Flasche. Es erfolgt der Ausschlag, ich habe das Potential 40 erreicht oder eigentlich überschritten und Sie sehen, wenn ich die Flasche entlade, den zugehörigen Funken.
Fußnote aus technischen Gründen im Text wiedergegeben. Re. Die eben angegebene Disposition ist aus mehreren Gründen zur wirklichen Messung des Potentials nicht geeignet. Das Thomsonsche absolute Elektrometer beruht auf einer sinnreichen Modifikation der elektrischen Wage von
Harris und
Volta. Von zwei großen planparallelen Platten ist die eine zur Erde abgeleitet, die andere auf das zu messende Potential gebracht. Ein kleines bewegliches Flächenstück
f der letzteren hängt an der Wage zur Bestimmung der Attraktion
P. Bei dem Plattenabstand
D ergibt sich
.
![]()
Die Schlagweite zwischen den Funkenkugeln einer Maschine wächst mit der Potentialdifferenz, wenn auch nicht proportional derselben. Die Schlagweite wächst rascher als die Potentialdifferenz. Bei einem Abstand der Funkenkugeln von 1 Cm. an dieser Maschine ist die Potentialdififerenz 110. Man kann sie leicht auf das Zehnfache bringen. Und welche bedeutende Potentialdifferenzen in der Natur vorkommen, sieht man daraus, daß die Schlagweite der Blitze bei Gewittern nach Kilometern zählt. Die Potentialdifferenzen bei galvanischen Batterien sind bedeutend kleiner, als jene an unserer Maschine, denn erst einige hundert Elemente geben einen Funken von mikroskopischer Schlagweite.
Wir wollen nun die gewonnenen Begriffe benützen, um eine andere wichtige Beziehung der elektrischen und mechanischen Vorgänge zu beleuchten. Wir wollen untersuchen, welche potentielle Energie oder welcher Arbeitsvorrat in einem geladenen Leiter, z. B. in einer Flasche, enthalten ist.
Schafft man eine Elektrizitätsmenge auf einen Leiter, oder ohne Bild gesprochen, erzeugt man durch Arbeit elektrische Kraft an einem Leiter, so vermag diese Kraft die Arbeit wiederzugeben, durch welche sie entstanden ist. Wie groß ist nun die Energie oder Arbeitsfähigkeit eines Leiters von bekannter Ladung Q und bekanntem Potential V?
Wir denken uns die genannte Ladung
Q in sehr kleine Teile
q,
q
1
q
2 .... geteilt, und dieselben nach einander auf den Leiter geschafft. Die erste sehr kleine
Menge
q gelangt ohne merkliche Arbeit hinauf, erzeugt aber ein kleines Potential
V
1. Zur Förderung der zweiten Menge brauchen wir dann schon die Arbeit
q
1
V
1 und analog für die folgenden Mengen die Arbeiten
q
2 V
2,
q
3 V
3 u. s. f. Da nun das Potential den zugeführten Mengen selbst proportional bis V ansteigt, so ergibt sich entsprechend unserer graphischen Darstellung (Fig. 41) die Gesamtarbeit W = I/2 QV, welche der gesamten Energie des geladenen Leiters entspricht. Mit Rücksicht auf die Gleichung
Q = CV, worin
C die Kapazität bedeutet, können wir auch sagen
![]()
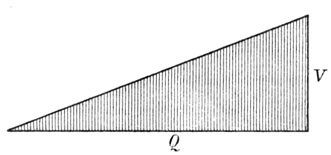
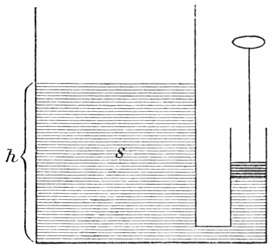
Fig. 41. Fig. 42.
Es wird vielleicht nützlich sein, den ausgeführten Gedanken noch durch eine Analogie aus dem Gebiete der Mechanik zu erläutern. Wenn wir eine Flüssigkeitsmenge
Q allmählich in ein zylindrisches Gefäß pumpen (Fig. 42), so steigt in diesem das Niveau ebenso allmählich. Je
mehr wir schon eingepumpt haben, mit desto größerem Druck müssen wir weiter pumpen, oder auf ein desto höheres Niveau müssen wir die Flüssigkeit heben. Die aufgespeicherte Arbeit wird wieder verwendbar, wenn das Flüssigkeitsgewicht
Q, welches bis zum Niveau
h reicht, wieder ausfließt. Diese Arbeit W entspricht dem Fall des ganzen Flüssigkeitsgewichts
Q um die mittlere Höhe h/2, oder um die Schwerpunktshöhe. Es ist W = 1/2 Qh. Und weil
Q =
K h, d. h. weil das Flüssigkeitsgewicht und die Höhe h proportional sind, ist auch
![]()
Betrachten wir als spezielles Beispiel unsere Flasche.
Die Kapazität ist C = 3700,
das Potential V = 110, demnach
die Menge Q = CV = 407.000 elektrostatische Einheiten,
und die Energie W = I/2 QV = 22,385,000 C.-G.-S.-Arbeitseinheiten.
Diese Arbeitseinheit des C.-G.-S.-System liegt unserm Gefühl fern, und ist für uns wenig anschaulich, da wir gewohnt sind, mit Gewichten zu operieren. Nehmen wir demnach als Arbeitseinheit ein Grammcentimeter, welche dem Druck eines Grammgewichtes auf die Wegstrecke von 1 cm entspricht, und welche rund 1000 mal größer ist als die vorher zu Grunde gelegte Einheit, so wird unsere Zahl rund 1000 mal kleiner. Und übergehen wir zu dem praktisch so geläufigen Kilogrammmeter als Arbeitseinheit, so ist dies wegen der 100mal größeren Wegstrecke und dem 1000mal größeren Gewicht, das wir nun zu Grunde legen, 100.000mal größer. Die Zahl für die Arbeit fällt also 100.000 mal kleiner aus, und wird rund 0.22 Kilogrammmeter. Wir können uns von dieser Arbeit sofort eine anschauliche Vorstellung verschaffen, wenn wir ein Kilogrammgewicht 22 cm tief fallen lassen.
Diese Arbeit wird also bei Ladung der Flasche geleistet, und kommt bei Entladung derselben nach Umständen teils als Schall, teils als mechanische Durchbrechung von Isolatoren, teils als Licht und Wärme u. s. w. zum Vorschein.
Die erwähnte große Batterie des physikalischen Institutes aus 16 Flaschen zu gleichem Potential geladen, liefert, obgleich der Entladungseffekt imposant ist, doch nur eine Gesamtarbeit von etwa 3 Kilogrammmeter.
Bei Entwicklung der eben dargelegten Gedanken sind wir durchaus nicht auf den von uns eingeschlagenen Weg beschränkt, welcher nur als ein zur Orientierung vorzugsweise geeigneter gewählt wurde. Der Zusammenhang unter den physikalischen Erscheinungen ist vielmehr ein so mannigfacher, daß man derselben Sache auf sehr verschiedene Weise beikommen kann. Namentlich hängen die elektrischen Erscheinungen mit allen übrigen so innig zusammen, daß man die Elektrizitätslehre billig die Lehre vom Zusammenhang der physikalischen Erscheinungen nennen könnte, was Ihnen die folgenden Vorträge ohne Zweifel recht nahe legen werden.
Was insbesondere das Prinzip der Erhaltung der Energie betrifft, welches die elektrischen mit den mechanischen Erscheinungen verknüpft, so möchte ich noch kurz auf zwei Wege aufmerksam machen, diesen Zusammenhang zu verfolgen.
Professor Rosetti hat vor einigen Jahren an einer durch Gewicht betriebenen Influenzmaschine, die er abwechselnd in elektrischem und unelektrischem Zustande mit gleicher Geschwindigkeit in Gang setzte, in beiden Fällen die aufgewendete mechanische Arbeit bestimmt, und war dadurch in den Stand gesetzt, die nach Abzug der Reibungsarbeit rein auf Elektrizitätsentwicklung entfallende mechanische Arbeit zu ermitteln.
Ich selbst habe den Versuch in modifizierter, und wie ich glaube, in vorteilhafter Form angestellt. Anstatt nämlich die Reibungsarbeit besonders zu bestimmen, habe ich den Apparat so eingerichtet, daß sie bei der Messung von selbst ausfällt, und gar nicht beachtet zu werden braucht. Die sogenannte fixe Scheibe der Maschine, deren Rotationsaxe vertikal steht, ist ähnlich wie ein Kronleuchter an drei gleich langen vertikalen Fäden von der Länge
l und dem Axenabstand
r aufgehängt. Nur wenn die Maschine erregt ist, erhält diese Scheibe, welche einen
Ponyschen Zaum vorstellt, durch die Wechselwirkung mit der rotierenden Scheibe eine Ablenkung
a und ein Drehungsmoment, welches durch
![]() ausgedrückt ist, wenn
P das
Scheibengewicht ist.
Dieses Drehungsmoment muß noch wegen der elektrischen Attraktion der erregten Scheiben korrigiert werden. Dies erreicht man, indem man das Scheibengewicht durch Zuleggewichte ändert, und noch eine Winkelablesung macht. Der Winkel
a wird durch einen auf die Scheibe gesetzten Spiegel bestimmt. Die bei n Umdrehungen aufgewendete Arbeit ist durch 2
n π D gegeben.
ausgedrückt ist, wenn
P das
Scheibengewicht ist.
Dieses Drehungsmoment muß noch wegen der elektrischen Attraktion der erregten Scheiben korrigiert werden. Dies erreicht man, indem man das Scheibengewicht durch Zuleggewichte ändert, und noch eine Winkelablesung macht. Der Winkel
a wird durch einen auf die Scheibe gesetzten Spiegel bestimmt. Die bei n Umdrehungen aufgewendete Arbeit ist durch 2
n π D gegeben.
Schließt man die Maschine in sich, wie es Rosetti getan hat, so erhält man einen kontinuierlichen Strom, der alle Eigenschaften eines sehr schwachen galvanischen Stromes hat, z. B. an einem eingeschalteten Multiplikator einen Ausschlag erzeugt u. s. w. Man kann nun direkt die zur Instandhaltung dieses Stromes aufgewendete mechanische Arbeit ermitteln.
Ladet man mit Hilfe der Maschine eine Flasche, so entspricht die Energie derselben, welche zur Funkenbildung, zur Durchbrechung von Isolatoren u. s. w. verwendet werden kann, nur einem Teil der aufgewendeten mechanischen Arbeit, indem ein anderer Teil im Schließungsbogen verbraucht wird. Es ist ein Bild der Kraft- oder richtiger der Arbeitsübertragung, welches diese Maschine mit eingeschalteter Flasche im Kleinen darbietet. Und in der Tat gelten hier ähnliche Gesetze für den ökonomischen Koëfficienten, wie sie für die großen Dynamomaschinen platzgreifen.
Fußnote aus technischen Gründen im Text wiedergegeben. Re.
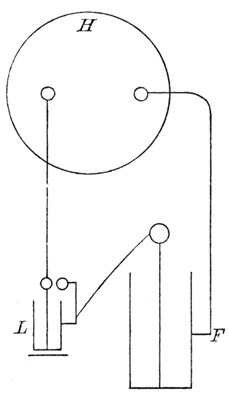
Fig. 43.
In unserm Experiment verhält sich die Flasche wie ein Akkumulator, der durch eine Dynamomaschine geladen wird. Welches Verhältnis zwischen der aufgewendeten und nutzbaren Arbeit besteht, wird durch folgende einfache Darstellung ersichtlich. Die
Holtbsche Maschine
H, Fig. 43, lade eine Maßflasche
L, welche nach
n Entladungen mit der Menge
q und dem Potential
v, die Flasche
F mit der Menge
Q zum Potential V geladen hat. Die Energie der Maßflaschen-Entladungen ist verloren, und jene der Flasche
F allein übrig. Demnach ist das Verhältnis der nutzbaren zur überhaupt aufgewendeten Arbeit:
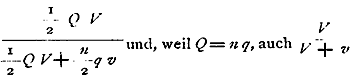 .
.
Schaltet man nun auch keine Maßflasche ein, so sind doch die Maschinenteile und Zuleitungsdrähte selbst solche Maßflaschen und es besteht die Formel fort
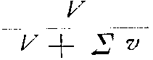 , in welcher
Σ v die Summe aller hintereinander geschalteten Potentialdifferenzen im Schließungskreise bedeutet.
, in welcher
Σ v die Summe aller hintereinander geschalteten Potentialdifferenzen im Schließungskreise bedeutet.
Ein anderes Mittel zur Untersuchung der elektrischen Energie ist die Umwandlung derselben in Wärme. Riess hat derartige Versuche mit Hilfe seines elektrischen Luft-Thermometers ausgeführt, und zwar vor langer Zeit schon (1838), als die mechanische Wärmetheorie noch nicht so populär war wie heute.
Wird die Entladung durch einen durch die Kugel des Luft-Thermometers gezogenen feinen Draht geleitet, so läßt sich eine Wärmeentwicklung nachweisen, welche dem schon erwähnten Ausdruck W = 1/2 QV proportional geht. Wenn es nun auch noch nicht gelungen ist, die gesamte Energie auf diese Weise in meßbare Wärme umzuwandeln, weil ein Teil in dem Funken in der Luft außerhalb des Thermometers verbleibt, so spricht doch alles dafür, daß die gesamte in allen Leiterteilen und Entladungswegen schließlich entwickelte Wärme das Äquivalent der Arbeit 1/2 QV sei.
Es kommt hierbei auch gar nicht darauf an, ob die elektrische Energie auf einmal oder teilweise, nach und nach, umgewandelt wird. Wenn z. B. von zwei gleichen Flaschen die eine mit der Menge Q zum Potential V geladen ist, so ist die vorhandene Energie 1/2 QV. Entladet man die Flasche in die andere, so sinkt wegen der doppelten Kapazität V auf V/2. Es verbleibt also die Energie 1/4 QV, während 1/4 QV im Entladungsfunken in Wärme umgewandelt wurde. Der Rest ist aber in beiden Flaschen gleich verteilt, so daß jede bei ihrer Entladung noch 1/8 QV in Wärme umzusetzen vermag.
Wir haben die Elektrizität in der beschränkten Erscheinungsform besprochen, welche den Forschern vor Volta allein bekannt war und die man, vielleicht nicht ganz glücklich, statische Elektrizität oder Spannungselektrizität genannt hat. Es versteht sich aber, daß die Natur der Elektrizität überall eine und dieselbe ist, daß ein wesentlicher Unterschied zwischen statischer und galvanischer Elektrizität nicht besteht. Nur die quantitativen Umstände sind in beiden Gebieten so sehr verschieden, daß in dem zweiten ganz neue Seiten der Erscheinung, wie z. B. die magnetischen Wirkungen deutlich hervortreten können, welche in dem ersten unbemerkt blieben, während umgekehrt wieder die statischen Anziehungen und Abstoßungen in dem zweiten Gebiete fast verschwinden. In der Tat kann man die magnetische Wirkung des Entladungsstromes einer Influenzmaschine leicht am Multiplikator nachweisen, doch hätte man schwerlich an diesem Strome die magnetische Wirkung entdecken können. Die statischen Fernwirkungen der Poldrähte eines galvanischen Elementes wären ebenfalls kaum zu beobachten, wenn die Erscheinung nicht schon von anderer Seite her in auffallender Form bekannt wäre.
Wollte man die beiden Gebiete in den Hauptzügen charakterisieren, so würde man sagen, daß in dem ersteren hohe Potentiale und kleine Mengen, in dem letzteren kleine Potentiale und große Mengen ins Spiel kommen. Eine sich entladende Flasche und ein galvanisches Element verhalten sich etwa wie eine Windbüchse und ein Orgelblasebalg. Erstere gibt plötzlich unter sehr hohem Druck eine kleine Luftquantität, letzterer allmählich unter sehr geringem Druck eine große Luftquantität frei.
Es würde zwar prinzipiell nichts im Wege stehen, auch im Gebiet der galvanischen Elektrizität die elektrostatischen Maße festzuhalten, und z. B. die Stromstärke zu messen durch die Zahl der elektrostatischen Feinheiten, welche in der Sekunde den Querschnitt passieren, allein dies wäre in doppelter Hinsicht unpraktisch. Erstens würde man die magnetischen Anhaltspunkte der Messung, welche der Strom bequem darbietet, unbeachtet lassen, und dafür eine Messung setzen, die sich an dem Strom nur schwer und mit geringer Genauigkeit ausführen läßt. Zweitens würde man eine viel zu kleine Einheit anwenden und dadurch in dieselbe Verlegenheit kommen, wie ein Astronom, der die Himmelsräume in Metern, statt in Erdradien und Erdbahnhalbmessern ausmessen wollte, denn der Strom, welcher nach magnetischem Maße (in C.-G.-S.) die Einheit darstellt, fördert etwa 30.000,000.000 (30 Tausend Millionen) elektrostatischer Einheiten in der Sekunde durch den Querschnitt. Deshalb müssen hier andere Maße zu Grunde gelegt werden. Dies auseinanderzusetzen gehört aber nicht mehr zu meiner Aufgabe. Es liegt die Bemerkung nahe, daß man mit jedem der Begriffe Q V, W unmittelbar an die Beobachtung anknüpfen kann. Die beiden andern Begriffe lassen sich dann durch den als Fundamentalbegriff gewählten und die nötigen Konstanten ausdrücken. Coulomb geht von dem Mengenbegriff, Cavendihs von dem Potentialbegriff aus, während Rieß (allerdings nicht mit vollem Bewußtsein) an den Energiebegriff anknüpft. Des letzteren Luftthermometer ist eigentlich ein Funken kalorimeter, welches sich mit Vorteil in die Form des Bunsenschen Eiskalometers bringen ließe, und das dann wohl noch zu andern Untersuchungen (Schmelz- und Dampfwärme der Metalle usw.) dienen könnte. Man befreit sich von Zufälligkeiten der Auffassung, indem man sich die Folgen einer Änderung der historischen Reihenfolge von einander unabhängiger Entdeckungen vergegenwärtigt. Vgl. »Erhaltung der Arbeit«, »Mechanik« und den folgenden Artikel XII. – 1902.