
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Vortrag gehalten im deutschen Kasino zu Prag im Winter 1871.
Ein alter Philosoph meinte, die Leute, welche über die Natur des Mondes sich den Kopf zerbrächen, kämen ihm vor, wie Menschen, welche die Verfassung und Einrichtung einer fernen Stadt besprächen, von der sie doch kaum mehr als den bloßen Namen gehört haben. Der wahre Philosoph, sagt er, müsse seinen Blick nach Innen wenden, sich und seine Begriffe von Moral studieren, daraus würde er wirklichen Nutzen ziehen. Dieses alte Rezept, glücklich zu werden, ließe sich in die deutsche Philistersprache etwa so übersetzen: Bleibe im Lande und nähre dich redlich.
Wenn nun dieser Philosoph aufstehen und wieder unter uns wandeln könnte, so würde er sich wundern, wie ganz anders die Dinge heute liegen.
Die Bewegungen des Mondes und anderer Weltkörper sind genau bekannt. Die Kenntnis der Bewegungen unseres eigenen Körpers ist lange noch nicht so vollendet. Die Gebirge und Gegenden des Mondes sind in genauen Karten verzeichnet. Eben fangen die Physiologen erst an, in den Gegenden unseres Hirns sich zurecht zu finden. Die chemische Beschaffenheit vieler Fixsterne ist bereits untersucht. Die chemischen Vorgänge des Tierkörpers sind viel kompliziertere und schwierigere Fragen. Die mécanique céleste ist da. Eine mécanique soziale oder eine mécanique morale von gleicher Zuverlässigkeit bleibt noch zu schreiben.
In der Tat, unser Philosoph würde eingestehen, daß wir Menschen Fortschritte gemacht haben. Allein wir haben sein Rezept nicht befolgt. Der Patient ist gesund geworden, er hat aber ungefähr das Gegenteil von dem getan, was der Herr Doktor verordnet hat.
Die Menschen sind nun von der ihnen entschieden widerratenen Reise in den Weltraum etwas klüger zurückgekehrt. Nachdem sie die einfachen großen Verhältnisse dort draußen im Reich kennen gelernt, fangen sie an, ihr kleines verzwacktes Ich mit kritischem Auge zu mustern. Es klingt absurd, ist aber wahr, nachdem wir über den Mond spekuliert, können wir an die Psychologie gehen. Wir mußten einfache und klare Ideen gewinnen, um uns in dem Komplizierten zurecht zu finden, und diese hat uns hauptsächlich die Astronomie verschafft.
Eine Schilderung der gewaltigen wissenschaftlichen Bewegung, welche von der Naturwissenschaft ausgehend, sich in das Gebiet der Psychologie erstreckt, hier zu versuchen, wäre Vermessenheit. Ich will es nur wagen, Ihnen an einigen der einfachsten Beispiele zu zeigen, wie man, von den Erfahrungen der physischen Welt ausgehend, in das Gebiet der Psychologie und zwar zuerst in das nächstliegende der Sinneswahrnehmung eindringen kann. Auch soll meine Ausführung keineswegs einen Maßstab für den Stand derartiger wissenschaftlicher Fragen abgeben.
Es ist eine bekannte Sache, daß manche Gegenstände uns gefällig erscheinen, andere nicht. Im allgemeinen gibt ein Produzieren nach einer bestimmten, konsequent festgehaltenen Regel etwas leidlich Hübsches. Wir sehen deshalb die Natur selbst, welche immer nach festen Regeln handelt, eine Menge solcher gefälliger Dinge hervorbringen. Täglich fallen dem Physiker in seinem Laboratorium die schönsten Schwingungsfiguren, Klangfiguren, Polarisationserscheinungen und Beugungsgestalten auf.
Eine Regel setzt immer eine Wiederholung voraus. Es spielt also die Wiederholung wohl eine Rolle im Angenehmen. Hiermit ist freilich das Wesen des Angenehmen nicht erschöpft. Die Wiederholung eines physikalischen Vorganges kann auch nur dann zur Quelle des Angenehmen werden wenn sie mit einer Wiederholung der Empfindung verbunden ist.
Ein Beispiel dafür, daß Wiederholung der Empfindung angenehm sein kann, bietet das Schreibheft jedes Schuljungen, welches eine Fundgrube für dergleichen Dinge ist, und in der Tat nur eines Abbé Domenech bedarf, um berühmt zu werden. Irgend eine noch so abgeschmackte Gestalt einige Male wiederholt und in eine Reihe gestellt, gibt immer ein leidliches Ornament.
Die angenehme Wirkung der Symmetrie beruht nun ebenfalls auf der Wiederholung der Empfindungen. Geben wir uns einen Augenblick diesem Gedanken hin, ohne zu glauben, daß wir damit das Wesen des Angenehmen oder gar des Schönen vollständig durchschauen.
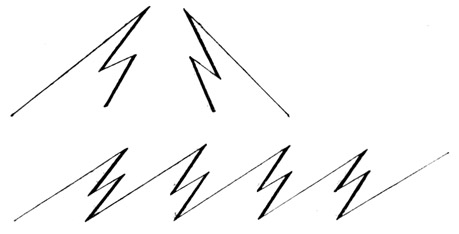
Fig. 25.
Verschaffen wir uns zunächst eine deutlichere Vorstellung von der Symmetrie. Hierzu ziehe ich aber ein lebendiges Bild einer Definition vor. Sie wissen, daß das Spiegelbild eines Gegenstandes eine große Ähnlichkeit mit dem Gegenstande selbst hat. Alle Größenverhältnisse und Formen sind dieselben. Doch besteht zwischen dem Gegenstande und seinem Spiegelbild auch ein gewisser Unterschied.
Bringen Sie Ihre rechte Hand vor den Spiegel, so erblicken Sie in demselben eine linke Hand. Ihr rechter Handschuh ergänzt sich vor dem Spiegel zu einem Paare; denn Sie könnten nimmermehr das Spiegelbild zur Bekleidung der rechten, sondern nur der linken Hand benützen, wenn es Ihnen leibhaftig vorgelegt würde. Ebenso gibt Ihr rechtes Ohr als Spiegelbild ein linkes, und sehr leicht gelangen Sie zu der Einsicht, daß überhaupt die linke Körperhälfte als Spiegelbild der rechten gelten könnte.
So wie nun an die Stelle eines fehlenden rechten Ohres niemals ein linkes gesetzt werden könnte, man müßte denn, das Ohrläppchen nach oben oder die Öffnung der Ohrmuschel nach hinten gekehrt, das Ohr ansetzen: so kann auch trotz aller Formengleichheit das Spiegelbild eines Gegenstandes nicht den Gegenstand vertreten. Kant hat zu einem andern Zwecke (Prolegomena zu einer jeden künftigen Metaphysik) auf diesen Fall hingewiesen.
Diese Verschiedenheit von Gegenstand und Spiegelbild hat einen einfachen Grund. Das Bild erscheint so weit hinter dem Spiegel, als der Gegenstand sich vor dem Spiegel befindet. Die Teile des Gegenstandes, welche gegen den Spiegel hin rücken, werden also auch im Bilde näher an die Spiegelebene heranrücken. Dadurch wird aber die Folge, die Ordnung der Teile im Spiegelbilde umgekehrt, wie man am besten an dem Bilde eines Uhrzifferblattes oder einer Schrift sieht.
Man kann nun leicht bemerken, daß, wenn man einen Punkt des Gegenstandes mit dem Spiegelbild desselben Punktes verbindet, diese Verbindungslinie senkrecht zum Spiegel ausfällt und durch denselben halbiert wird. Dies gilt für alle entsprechenden Punkte von Gegenstand und Spiegelbild.
Wenn man nun einen Gegenstand durch eine Ebene so in zwei Hälften zerlegen kann, daß jede Hälfte das Spiegelbild der andern in der spiegelnden Teilungsebene sein könnte, so nennt man diesen Gegenstand symmetrisch und die erwähnte Teilungsebene die Symmetrieebene.
Ist die Symmetrieebene vertikal, so kann man sagen, der Körper sei von vertikaler Symmetrie. Ein Beispiel dafür ist ein gotischer Dom.
Ist die Symmetrieebene horizontal, so wollen wir den betreffenden Gegenstand horizontal symmetrisch nennen. Eine Landschaft an einem See nebst ihrem Spiegelbilde in dem See ist ein System von horizontaler Symmetrie.
Hier zeigt sich nun sofort ein bemerkenswerter Unterschied. Die vertikale Symmetrie eines gotischen Domes fällt uns sofort auf, während man am Rhein auf und ab reisen kann, ohne die Symmetrie zwischen Bild und Gegenstand recht gewahr zu werden. Die Vertikalsymmetrie ist gefällig, während die Horizontalsymmetrie gleichgiltig ist, und nur von dem erfahrenen Auge bemerkt wird.
Woher kommt dieser Unterschied? Ich sage daher daß die Vertikalsymmetrie eine Wiederholung derselben Empfindung bedingt, die Horizontalsymmetrie aber nicht. Daß dem so sei, will ich sofort nachweisen.
Betrachten wir folgende Buchstaben:
d b
q p
Es ist eine Müttern und Lehrern bekannte Tatsache, daß Kinder bei ihren ersten Schreib- und Leseversuchen d und b, ebenso q und p fort und fort verwechseln; nie hingegen d, und q oder b und p. Nun sind d und b ebenso wie q und p die beiden Hälften einer vertikal symmetrischen, hingegen d und q, sowie b und p die beiden Hälften einer horizontal symmetrischen Figur. Zwischen den ersteren tritt Verwechslung ein, was nur zwischen solchen Dingen möglich ist, welche gleiche oder ähnliche Empfindungen erregen.
Man findet häufig Figuren zur Garten- oder Salonverzierung, zwei Blumenträgerinnen, von welchen die eine in der rechten, die andere in der linken Hand den Blumenkorb trägt. Wenn man nun nicht sehr aufmerksam ist, verwechselt man diese Figuren fortwährend mit einander.
Während man die Umkehrung von rechts nach links meist gar nicht merkt, verhält sich das Auge nicht so gleichgiltig gegen eine Umkehrung von oben nach unten. Ein von oben nach unten umgekehrtes menschliches Gesicht ist kaum als solches wiederzuerkennen und hat etwas durchaus Fremdes. Dies liegt nicht nur in der Ungewohnheit des Anblickes, denn es ist ebenso schwer, eine umgekehrte Arabeske, bei welcher die Gewohnheit gar nichts zu sagen hat, wiederzuerkennen. Hierauf beruhen die bekannten Scherze, welche man sich mit den Porträts unbeliebter Persönlichkeiten erlaubt, die man so zeichnet, daß bei aufrechter Stellung dieses Blattes sich ein getreues Conterfei, bei Umkehrung desselben aber irgend ein populäres Tier präsentiert.
Es ist also Tatsache, die beiden Hälften einer vertikal symmetrischen Figur werden sehr leicht mit einander verwechselt und bedingen also wahrscheinlich sehr ähnliche Empfindungen. Es handelt sich also darum, anzugeben, warum die beiden Hälften einer vertikal symmetrischen Figur gleiche oder ähnliche Empfindungen hervorbringen. Die Antwort darauf ist die: Weil unser Sehapparat, bestehend aus zwei Augen, selbst vertikal symmetrisch ist.
So ähnlich ein Auge auch äußerlich dem andern ist, so sind sie doch nicht gleich. Das rechte Auge des Menschen kann die Stelle des linken nicht vertreten, so wenig wie wir unsere beiden Ohren oder Hände vertauschen können. Man kann künstlich die Rolle der beiden Augen vertauschen und befindet sich dann sofort in einer neuen ganz ungewohnten Welt. Alles Erhabene erscheint uns dann hohl und alles Hohle erhaben, das Fernere näher, das Nähere ferner u. s. w.
Das linke Auge ist das Spiegelbild des rechten, und namentlich ist die lichtempfindende Netzhaut des linken Auges in allen ihren organischen Einrichtungen ein Spiegelbild der rechten Netzhaut.
Die Linse des Auges entwirft wie eine laterna magica ein Bild der Gegenstände auf der Netzhaut. Und Sie können sich nun die lichtempfindende Netzhaut mit ihren unzähligen Nerven wie eine Hand mit unzähligen Fingern denken, bestimmt, das Lichtbild zu tasten. Die Nervenenden sind nun wie die Finger verschieden. Die beiden Netzhäute verhalten sich wie eine rechte und linke tastende Hand.
Denken Sie sich etwa die rechte Hälfte eines T hier:
![]() . Statt der beiden Netzhäute, auf welche beide dieses Bild fällt, denken Sie sich meine beiden ausgestreckten tastenden Hände. Das
. Statt der beiden Netzhäute, auf welche beide dieses Bild fällt, denken Sie sich meine beiden ausgestreckten tastenden Hände. Das
![]() , mit der rechten Hand angefaßt, gibt nun eine andere Empfindung, als mit der linken Hand gefaßt, denn es kommt auch auf die tastenden Stellen an. Kehren
wir nun dieses Zeichen von rechts nach links um
, mit der rechten Hand angefaßt, gibt nun eine andere Empfindung, als mit der linken Hand gefaßt, denn es kommt auch auf die tastenden Stellen an. Kehren
wir nun dieses Zeichen von rechts nach links um
![]() , so gibt es nun dieselbe Empfindung in der linken Hand, die es früher in der rechten gab. Es wiederholt sich die Empfindung.
, so gibt es nun dieselbe Empfindung in der linken Hand, die es früher in der rechten gab. Es wiederholt sich die Empfindung.
Nehmen wir ein ganzes T, so löst die rechte Hälfte in der rechten Hand dieselbe Empfindung aus, welche die linke Hälfte in der linken Hand auslöst und. umgekehrt.
Die symmetrische Figur gibt dieselbe Empfindung zweimal.
Stürze ich das T so:
![]() oder kehre ich das halbe T nun etwa so:
oder kehre ich das halbe T nun etwa so:
![]() , so kann ich, so lange ich die Lage meiner Hände nicht wesentlich verändere, diese Betrachtung nicht mehr anwenden.
, so kann ich, so lange ich die Lage meiner Hände nicht wesentlich verändere, diese Betrachtung nicht mehr anwenden.
Die Netzhäute sind in der Tat ganz wie meine beiden Hände. Auch sie haben eine Art Daumen, wenn gleich zu Tausenden und Zeigefinger, wenn gleich wieder zu Tausenden, sagen wir etwa die Daumen nach der Nasen-, die übrigen Finger nach der Außenseite zu.
Ich hoffe, Ihnen hiermit vollständig klar gemacht zu haben, wie die gefällige Wirkung der Symmetrie auf Wiederholung der Empfindung beruht, und wie ferner diese Wirkung bei symmetrischen Gestalten auch nur da eintritt, wo es eine Wiederholung der Empfindung gibt. Die angenehme Wirkung regelmäßiger Gestalten, der Vorzug, welcher den geraden Linien, namentlich den vertikalen und horizontalen vor beliebigen anderen eingeräumt wird, beruht auf einem ähnlichen Grunde. Die gerade Linie kann in horizontaler und in vertikaler Lage auf beiden Netzhäuten dasselbe Bild entwerfen, welches zudem auf einander symmetrisch entsprechende Stellen fällt. Hierauf beruht, wie es scheint, der psychologische Vorzug der Geraden vor der Krummen und nicht etwa auf der Eigenschaft, die Kürzeste zwischen zwei Punkten zu sein. Die Gerade wird, um es kurz zu sagen, als symmetrisch zu sich selbst empfunden, so wie die Ebene. Das Krumme empfinden wir als Abweichung vom Geraden, als Abweichung von der Symmetrie. Der Umstand, daß man den ersten und zweiten Differentialquotienten einer Kurve unmittelbar sieht, die höheren aber nicht, erklärt sich einfach. Der erste gibt die Lage der Tangente, die Abweichung der Geraden von der Symmetrielage, der zweite die Abweichung der Kurve von den Geraden. – Es ist vielleicht nicht unnütz, hier zu bemerken, daß die gewöhnliche Prüfung des Lineals und ebener Platten (durch umgekehrtes Anlegen) in der Tat die Abweichung von der Symmetrie zu sich selbst ermittelt. Wenn nun auch von Geburt Einäugige ein gewisses Gefühl für Symmetrie haben, so ist dies allerdings ein Rätsel. Freilich kann das optische Symmetriegefühl, wenn auch zunächst durch die Augen erworben, nicht auf diese beschränkt bleiben. Es muß sich wohl auch noch in anderen Teilen des Organismus durch mehrtausendjährige Übung des Menschengeschlechtes festsetzen, und kann dann nicht mit dem Verlust des einen Auges sofort wieder verschwinden.
Alles das gründet sich aber doch im ganzen, wie es scheint, auf die eigentümliche Struktur unserer Augen. Man sieht leicht ein, daß unsere Vorstellungen von schön und unschön sofort eine Veränderung erfahren müßten, wenn unsere Augen anders würden. Ist die ganze Betrachtung richtig, so wird man notwendig an dem sogenannten ewig Schönen etwas irre. Es ist dann kaum zu glauben, daß die Kultur, welche dem Menschenleib ihren unverkennbaren Stempel aufprägt, nicht auch die Vorstellungen vom Schönen ändern sollte. Mußte doch ehedem alles musikalisch Schöne sich in dem engen Rahmen einer fünftönigen Leiter entwickeln.
Die Erscheinung, daß Wiederholung der Empfindungen angenehm wirkt, beschränkt sich nicht auf das Sichtbare. Der Musiker und Physiker wissen heute beide, daß die harmonische oder melodische Hinzufügung eines Klanges zu einem andern dann angenehm berührt, wenn der neu hinzugefügte Klang einen Teil der Empfindung wiedergibt, welche der frühere erregt. Wenn ich zum Grundtone die Oktave hinzufüge, so höre ich in der Oktave einen Teil dessen, was im Grundtone zu hören ist. Dies hier genauer auszuführen, ist jedoch nicht mein Zweck. Wir wollen uns vielmehr für heute die Frage vorlegen, ob etwas Ähnliches wie die Symmetrie der Gestalten nicht auch im Reiche der Töne vorkommt.
Betrachten Sie ein Klavier im Spiegel.
Sie werden leicht bemerken, daß Sie ein solches Klavier in Wirklichkeit noch nicht gesehen haben, denn es hat seine hohen Töne links, seine tiefen rechts. Ein solches Klavier wird nicht gebaut.
Wenn Sie nun an ein solches Spiegelklavier hintreten und in Ihrer gewöhnlichen Weise spielen wollten, so würde offenbar jeder Tonschritt, den Sie nach oben auszuführen meinen, ein ebenso großer Tonschritt nach unten sein. Der Effekt wäre nicht wenig überraschend.
Für den geübten Musiker, welcher gewöhnt ist, beim Anschlag bestimmter Tasten auch bestimmte Töne zu vernehmen, ist es schon ein sehr frappantes Schauspiel, dem Spieler im Spiegel zuzusehen und zu beobachten, wie er gerade immer das Gegenteil von dem tut, was man hört.
Noch merkwürdiger aber wäre der Effekt, wenn Sie versuchen würden, auf dem Spiegelklavier eine Harmonie anzuschlagen. Für die Melodie ist es nicht einerlei, ob ich einen Tonschritt hinauf oder den gleichen hinab ausführe. Für die Harmonie kann ein so großer Unterschied durch die Umkehrung nicht entstehen. Ich behalte immer die gleiche Konsonanz, ob ich zu einem Grundton eine Ober- oder Unterterz hinzufüge. Nur die Ordnung der Intervalle einer Harmonie wird umgekehrt.
In der Tat, wenn wir auf dem Spiegelklavier einen Gang in Dur ausführen, vernehmen wir einen Klang in Moll und umgekehrt.
Es handelt sich nun darum, die besprochenen Experimente auszuführen. Statt nun auf dem Klavier im Spiegel zu spielen, was unmöglich ist, oder statt uns ein solches Klavier bauen zu lassen, was ziemlich kostspielig wäre, können wir unsere Versuche einfacher auf folgende Art anstellen:
1. Wir spielen auf unserem gewöhnlichen Klavier, sehen in den Spiegel und spielen auf demselben Klavier nochmals, was wir in dem Spiegel gesehen haben. Dadurch verwandeln wir alle Tonschritte nach oben in gleich große Tonschritte nach unten. Wir spielen einen Satz und dann den in Bezug auf die Tastatur symmetrischen Satz.
2. Wir legen unter das Notenblatt einen Spiegel, in welchem sich die Noten wie in einer Wasserfläche abbilden, und spielen aus dem Spiegel. Dadurch werden ebenfalls alle Schritte nach oben in gleich große Schritte nach unten umgekehrt.
3. Wir kehren das Notenblatt um und lesen von rechts nach links und von unten nach oben. Hierbei haben wir alle Kreuze als b und alle b als Kreuze anzusehen, weil sie halben Linien und Zwischenräumen entsprechen. Außerdem kann man bei Verwendung des Notenblattes nur den Baßschlüssel gebrauchen, weil in diesem allein die Tonschritte bei der symmetrischen Umkehrung nicht verändert werden.
Aus den in der Notenbeilage S. 113 folgenden Beispielen können Sie den Effekt dieser Experimente entnehmen. Die obere Zeile enthält den einen, die untere Zeile den symmetrisch umgekehrten Satz.
Die Wirkung unseres Verfahrens läßt sich kurz bezeichnen. Die Melodie wird unkenntlich, die Harmonie erfährt eine Transposition aus Dur in Moll oder umgekehrt. Das Studium dieser interessanten Tatsache, welche den Physikern und Musikern bekannt ist, wurde in neuester Zeit wieder durch v. Öttingen angeregt. A. v. Öttingen, Harmoniesystem in dualer Entwickelung. Dorpat 1866.

Obgleich ich nun in allen obigen Beispielen die Schritte nach oben in gleich große nach unten verkehrt, also wie man mit Recht sagen kann, zu jedem Satz den symmetrischen ausgeführt habe, so merkt das Ohr doch wenig oder nichts von Symmetrie. Die Umkehrung aus Dur in Moll ist die einzige Andeutung der Symmetrie, welche übrig bleibt. Die Symmetrie ist da für den Verstand sie fehlt für die Empfindung. Für das Ohr gibt es keine Symmetrie, weil eine Umkehrung der Tonschritte keine Wiederholung der Empfindung bedingt. Hätten wir ein Ohr für die Höhe und eines für die Tiefe, wie wir ein Auge für rechts und eines für links haben, so würden sich auch symmetrische Tongebilde hierzu finden. Der Gegensatz von Dur und Moll beim Ohr entspricht einer Umkehrung von oben nach unten beim Auge, welche auch nur für den Verstand Symmetrie ist, aber nicht als solche empfunden wird.
Zur Vervollständigung des Ganzen will ich für den mathematisch unterrichteten Teil meiner verehrten Zuhörer noch eine kurze Bemerkung hinzufügen.
Unsere Notenschrift ist im wesentlichen eine graphische Darstellung des Musikstückes in Form von Kurven, wobei die Zeit als Abscisse, der Logarithmus der Schwingungszahl als Ordinate aufgetragen wird. Die Abweichungen der Notenschrift von diesem Prinzipe sind nur solche, welche entweder die Übersicht erleichtern, oder einen historischen Grund haben.
Wenn man nun noch bemerkt, daß auch die Empfindung der Tonhöhe proportional geht dem Logarithmus der Schwingungszahl, sowie daß die Tastenabstände den Differenzen der Logarithmen der Schwingungszahlen entsprechen: so liegt darin die Berechtigung, die im Spiegel gelesenen Harmonien und Melodien in gewissem Sinne symmetrisch zu den Originalen zu nennen.
Ich wollte Ihnen durch diese höchst fragmentarische Auseinandersetzung nur zu Gemüte führen, daß die Fortschritte der Naturwissenschaften für jene Teile der Psychologie, die es nicht verschmäht haben, sich mit denselben in Beziehung zu setzen, nicht ohne Nutzen geblieben sind. Dafür fängt aber auch die Psychologie an, die mächtigen Anregungen, welche sie von der Naturwissenschaft erhalten hat, gleichsam wie zum Danke zurückzugeben.
Jene Theorien der Physik, welche alle Erscheinungen auf Bewegung und Gleichgewicht kleinster Teile zurückführen, die sogenannten Moleculartheorien, sind durch die Fortschritte der Theorie der Sinne und des Raumes bereits etwas ins Schwanken geraten, und man kann sagen, daß ihre Tage gezählt seien.
Ich habe anderwärts zu zeigen versucht, daß die Tonreihe nichts weiter sei, als eine Art Raum, jedoch von einer einzigen (und zwar einseitigen) Dimension. Wenn nun jemand, der bloß hören würde, versuchen wollte, sich eine Weltanschauung in seinem linearen Raume zu entwickeln, so würde er damit beträchtlich zu kurz kommen, indem sein Raum nicht im stande wäre, die Vielseitigkeit der wirklichen Beziehungen zu fassen. Es ist aber nicht mehr berechtigt, wenn wir meinen, die gesamte Welt, auch so weit sie nicht gesehen werden kann, in den Raum unseres Auges pressen zu können. In diesem Falle befinden sich aber sämtliche Moleculartheorien. Wir besitzen einen Sinn, welcher in Bezug auf die Vielseitigkeit der Beziehungen, welche er fassen kann, reicher ist, als jeder andere. Es ist unser Verstand. Dieser steht über den Sinnen. Er allein ist im stande, eine dauerhafte und ausreichende Weltanschauung zu begründen. Die mechanische Weltanschauung hat seit Galilei Gewaltiges geleistet. Doch wird sie jetzt einem freieren Blicke Platz machen müssen. Dieser wird von selbst dazu führen, daß man die Abhängigkeit der Naturerscheinungen von einander statt räumlich und zeitlich durch bloße Zahlenbeziehungen ausdrücken wird. – Vgl. Meine Note in Fichtes Zeitschrift für Philosophie 1866. Vgl. auch Artikel XIII. Das hier weiter auszuführen, kann nicht meine Absicht sein.
Ich wollte Ihnen nur einen andern Punkt klar machen. Jene Weisung unseres zitierten Philosophen, sich auf das Nächstliegende und Nützliche beim Forschen zu beschränken, welche in dem heutigen Ruf der Forscher nach Selbstbeschränkung und Teilung der Arbeit einigermaßen einen Wiederklang findet – es ist nicht immer an der Zeit, sie zu befolgen. Wir quälen uns in unserer Stube vergebens ab, ein Werk zu stande zu bringen, und die Mittel, es zu vollenden, liegen vielleicht vor der Türe.
Muß der Forscher schon ein Schuster sein, der nur an seinem Leisten klopft, so darf er doch vielleicht ein Schuster sein wie Hans Sachs, der es nicht verschmäht, nach des Nachbars Werk zu sehen, und darüber seine Glossen zu machen. Dies zu meiner Entschuldigung, wenn ich mir für heute erlaubt, über meinen Leisten hinweg zu sehen. Weitere Ausführungen über die hier besprochenen Probleme finden sich in meiner Schrift: » Beiträge zur Analyse der Empfindungen.« Jena 1886. 3. Aufl. 1902. Auch J. P. Soret, » Sur la perception du beau,« (Geneve 1892) betrachtet die Wiederholung als ein Prinzip der Ästhetik. Sorets Ausführungen über Ästhetik sind weitläufiger als die meinigen. In Bezug auf die psychologische und physiologische Begründung des Prinzipes glaube ich jedoch tiefer gegangen zu sein. – Zum erstenmal wurden die hier dargelegten Gedanken ausgesprochen in dem folgenden Artikel VIII.