Raum und Kraft

Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++

Über den Ursprung und die Bedeutung der geometrischen Axiome

Die Tatsache, daß eine Wissenschaft von der Art bestehen und in der Weise aufgebaut werden kann, wie es bei der Geometrie der Fall ist, hat von jeher die Aufmerksamkeit aller derer, welche für die prinzipiellen Fragen der Erkenntnistheorie Interesse fühlten, im höchsten Grade in Anspruch nehmen müssen. Unter allen Zweigen menschlicher Wissenschaft gibt es keine zweite, die gleich ihr fertig, wie eine erzgerüstete Minerva aus dem Haupte des Zeus, hervorgesprungen erscheint, keine, vor deren vernichtender Ägis Widerspruch und Zweifel so wenig ihre Augen aufzuschlagen wagten. Dabei fällt ihr in keiner Weise die mühsame und langwierige Aufgabe zu, Erfahrungstatsachen sammeln zu müssen, wie es die Naturwissenschaften im engeren Sinne zu tun haben, sondern die ausschließliche Form ihres wissenschaftlichen Verfahrens ist die Deduktion. Schluß wird aus Schluß entwickelt, und doch zweifelt schließlich niemand von gesunden Sinnen daran, daß diese geometrischen Sätze ihre sehr praktische Anwendung auf die uns umgebende Wirklichkeit finden müssen. Die Feldmeßkunst wie die Architektur, die Maschinenbaukunst wie die mathematische Physik, sie berechnen fortdauernd Raumverhältnisse der verschiedensten Art nach geometrischen Sätzen; sie erwarten, daß der Erfolg ihrer Konstruktionen und Versuche sich diesen Rechnungen füge, und noch ist kein Fall bekannt geworden, wo sie sich in dieser Erwartung getäuscht hätten, vorausgesetzt, daß sie richtig und mit ausreichenden Daten gerechnet hatten.

So ist denn auch die Tatsache, daß Geometrie besteht und solches leistet, in dem Streite über diejenige Frage, welche gleichsam den Kernpunkt aller Gegensätze der philosophischen Systeme bildet, immer benutzt worden, um an einem imponierenden Beispiele zu erweisen, daß ein Erkennen von Sätzen realen Inhalts ohne entsprechende aus der Erfahrung hergenommene Grundlage möglich sei. Namentlich bilden bei der Beantwortung von Kants berühmter Frage: »Wie sind synthetische Sätze a priori möglich?« die geometrischen Axiome wohl diejenigen Beispiele, welche am evidentesten zu zeigen schienen, daß überhaupt synthetische Sätze a priori möglich seien. Weiter gilt ihm der Umstand, daß solche Sätze existieren und sich unserer Überzeugung mit Notwendigkeit aufdrängen, als Beweis dafür, daß der Raum eine a priori gegebene Form aller äußeren Anschauung sei. Er scheint dadurch für diese a priori gegebene Form nicht nur den Charakter eines rein formalen und an sich inhaltsleeren Schema in Anspruch zu nehmen, in welches jeder beliebige Inhalt der Erfahrung passen würde, sondern auch gewisse Besonderheiten des Schema mit einzuschließen, die bewirken, daß eben nur ein in gewisser Weise gesetzmäßig beschränkter Inhalt in dasselbe eintreten und uns anschaubar werden könne.

Eben dieses erkenntnistheoretische Interesse der Geometrie ist es nun, welches mir den Mut gibt in einer Versammlung, deren Mitglieder nur zum kleinsten Teile tiefer, als es der Schulunterricht mit sich brachte, in mathematische Studien eingedrungen sind, von geometrischen Dingen zu reden. Glücklicher Weise wird das, was der Gymnasialunterricht an geometrischen Kenntnissen zu lehren pflegt, genügen, um Ihnen wenigstens den Sinn der im folgenden zu besprechenden Sätze verständlich zu machen.

Ich beabsichtige nämlich Ihnen Bericht zu erstatten über eine Reihe sich aneinander schließender neuerer mathematischer Arbeiten, welche die geometrischen Axiome, ihre Beziehungen zur Erfahrung und die logische Möglichkeit, sie durch andere zu ersetzen, betreffen.

Da die darauf bezüglichen Originalarbeiten der Mathematiker – zunächst nur bestimmt, Beweise für den Sachverständigen in einem Gebiet zu führen, welches eine höhere Kraft der Abstraktion in Anspruch nimmt als irgendein anderes–dem Nichtmathematiker ziemlich unzugänglich sind, so will ich versuchen auch für einen solchen anschaulich zu machen, um was es sich handelt. Ich brauche wohl nicht zu bemerken, daß meine Auseinandersetzung keinen Beweis von der Richtigkeit der neuen Einsichten geben soll. Wer einen solchen sucht, der muß sich schon die Mühe nehmen, die Originalarbeiten zu studieren.

Wer einmal durch die Pforten der ersten elementaren Sätze in die Geometrie, das heißt die mathematische Lehre vom Raum, eingetreten ist, der findet vor sich auf seinem weiteren Weg jene lückenlose Kette von Schlüssen, von denen ich vorher gesprochen habe, durch welche immer mannigfachere und verwickeltere Raumformen ihre Gesetze empfangen. Aber in jenen ersten Elementen werden einige Sätze aufgestellt, von denen die Geometrie selbst erklärt, daß sie sie nicht beweisen könne; daß sie nur darauf rechnen müsse, jeder, der den Sinn dieser Sätze verstehe, werde ihre Richtigkeit zugeben. Das sind die sogenannten Axiome der Geometrie. Zu diesen gehört zunächst der Satz, daß, wenn man die kürzeste Linie, die zwischen zwei Punkten gezogen werden kann, eine gerade Linie nennt, es zwischen zwei Punkten nur eine und nicht zwei verschiedene solche gerade Linien geben könne. Es ist ferner ein Axiom, daß durch je drei Punkte des Raumes, die nicht in einer geraden Linie liegen, eine Ebene gelegt werden kann, das heißt eine Fläche, in welche jede gerade Linie, die zwei ihrer Punkte verbindet, ganz hinein fällt. Ein anderes vielbesprochenes Axiom sagt aus, daß durch einen außerhalb einer geraden Linie liegenden Punkt nur eine einzige und nicht zwei verschiedene, jener ersten parallele, Linien gelegt werden können. Parallel aber nennt man zwei Linien, die in ein und derselben Ebene liegen und sich niemals schneiden, so weit sie auch verlängert werden mögen. Außerdem sprechen die geometrischen Axiome Sätze aus, welche die Anzahl der Dimensionen sowohl des Raumes als seiner Flächen, Linien, Punkte bestimmen, und den Begriff der Kontinuität dieser Gebilde erläutern, wie die Sätze, daß die Grenze eines Körpers eine Fläche, die einer Fläche eine Linie, die einer Linie ein Punkt, und der Punkt unteilbar ist; ferner die Sätze, daß durch Bewegung eines Punktes eine Linie, durch Bewegung einer Linie eine Linie oder Fläche, durch Bewegung einer Fläche eine Fläche oder ein Körper, durch Bewegung eines Körpers aber immer nur wieder ein Körper beschrieben werde.

Woher kommen nun solche Sätze, unbeweisbar und doch unzweifelhaft richtig im Felde einer Wissenschaft, wo sich alles andere der Herrschaft des Schlusses hat unterwerfen lassen? Sind sie ein Erbteil aus der göttlichen Quelle unserer Vernunft, wie die idealistischen Philosophen meinen, oder ist der Scharfsinn der bisher aufgetretenen Generationen von Mathematikern nur noch nicht ausreichend gewesen den Beweis zu finden? Natürlich versucht jeder neue Jünger der Geometrie, der mit frischem Eifer an diese Wissenschaft herantritt, der Glückliche zu sein, welcher alle Vorgänger überflügelt. Auch ist es ganz recht, daß ein jeder sich von neuem daran versucht; denn nur durch die Fruchtlosigkeit der eigenen Versuche konnte man sich bei der bisherigen Sachlage von der Unmöglichkeit des Beweises überzeugen. Leider finden sich von Zeit zu Zeit auch immer einzelne Grübler, welche sich so lange und tief in verwickelte Schlußfolgen verstricken, bis sie die begangenen Fehler nicht mehr entdecken können und die Sache gelöst zu haben glauben. Namentlich der Satz von den Parallelen hat eine große Zahl scheinbarer Beweise hervorgerufen.

Die größte Schwierigkeit in diesen Untersuchungen bestand und besteht immer darin, daß sich mit den logischen Begriffsentwickelungen gar zu leicht Ergebnisse der alltäglichen Erfahrung als scheinbare Denknotwendigkeiten vermischten, so lange die einzige Methode der Geometrie die von Euklides gelehrte Methode der Anschauung war. Namentlich ist es außerordentlich schwer, auf diesem Wege vorschreitend sich überall klarzumachen, ob man in den Schritten, die man für die Beweisführung nacheinander vorschreibt, nicht unwillkürlich und unwissentlich gewisse allgemeinste Ergebnisse der Erfahrung zu Hilfe nimmt, welche die Ausführbarkeit gewisser vorgeschriebener Teile des Verfahrens uns schon praktisch gelehrt haben. Der wohlgeschulte Geometer fragt bei jeder Hilfslinie, die er für irgendeinen Beweis zieht, ob es auch immer möglich sein wird eine Linie von der verlangten Art zu ziehen. Bekanntlich spielen die Konstruktionsaufgaben in dem System der Geometrie eine wesentliche Rolle. Oberflächlich betrachtet sehen dieselben aus wie praktische Anwendungen, welche man zur Einübung der Schüler hineingesetzt hat. In Wahrheit aber stellen sie die Existenz gewisser Gebilde fest. Sie zeigen, daß Punkte, gerade Linien oder Kreise von der Art, wie sie in der Aufgabe zu konstruieren verlangt werden, entweder unter allen Bedingungen möglich sind, oder bestimmen die etwa vorhandenen Ausnahmefälle. Der Punkt, um den sich die im folgenden zu besprechenden Untersuchungen drehen, ist wesentlich dieser Art. Die Grundlage aller Beweise in der Euklidschen Methode ist der Nachweis der Kongruenz der betreffenden Linien, Winkel, ebenen Figuren, Körper usw. Um die Kongruenz anschaulich zu machen, stellt man sich vor, daß die betreffenden geometrischen Gebilde zueinander hinbewegt werden, natürlich ohne ihre Form und Dimensionen zu verändern. Daß dies in der Tat möglich und ausführbar sei, haben wir alle von frühester Jugend an erfahren. Wenn wir aber Denknotwendigkeiten auf diese Annahme freier Beweglichkeit fester Raumgebilde mit unveränderter Form nach jeder Stelle des Raumes hin bauen wollen, so müssen wir die Frage aufwerfen, ob diese Annahme keine logisch unerwiesene Voraussetzung einschließt. Wir werden gleich nachher sehen, daß sie in der Tat eine solche einschließt, und zwar eine sehr folgenreiche. Wenn sie das aber tut, so ist jeder Kongruenzbeweis auf eine nur aus der Erfahrung genommene Tatsache gestützt.

Ich führe diese Überlegungen hier zunächst nur an, um klarzumachen, auf welche Schwierigkeiten wir bei der vollständigen Analyse aller von uns gemachten Voraussetzungen nach der Methode der Anschauung stoßen. Ihnen entgehen wir, wenn wir die von der neueren rechnenden Geometrie ausgearbeitete analytische Methode auf die Untersuchung der Prinzipien anwenden. Die ganze Ausführung der Rechnung ist eine rein logische Operation; sie kann keine Beziehung zwischen den der Rechnung unterworfenen Größen ergeben, die nicht schon in den Gleichungen, welche den Ansatz der Rechnung bilden, enthalten ist. Die erwähnten neueren Untersuchungen sind deshalb fast ausschließlich mittelst der rein abstrakten Methode der analytischen Geometrie geführt worden.

Übrigens läßt sich nun doch, nachdem die abstrakte Methode die Punkte, auf die es ankommt, kennen gelehrt hat, einigermaßen eine Anschauung dieser Punkte geben; am besten, wenn wir in ein engeres Gebiet herabsteigen, als unsere eigene Raumwelt ist. Denken wir uns–darin liegt keine logische Unmöglichkeit–verstandbegabte Wesen von nur zwei Dimensionen, die an der Oberfläche irgendeines unserer festen Körper leben und sich bewegen. Wir nehmen an, daß sie nicht die Fähigkeit haben, irgend etwas außerhalb dieser Oberfläche wahrzunehmen, wohl aber Wahrnehmungen zu machen, ähnlich den unserigen, innerhalb der Ausdehnung der Fläche, in der sie sich bewegen. Wenn sich solche Wesen ihre Geometrie ausbilden, so würden sie ihrem Raume natürlich nur zwei Dimensionen zuschreiben. Sie würden ermitteln, daß ein Punkt, der sich bewegt, eine Linie beschreibt, und eine Linie, die sich bewegt, eine Fläche, was für sie das vollständigste Raumgebilde wäre, das sie kennen. Aber sie würden sich ebenso wenig eine Vorstellung machen können von einem weiteren räumlichen Gebilde, das entstände, wenn eine Fläche sich aus ihrem flächenhaften Raume herausbewegte, als wir es können von einem Gebilde, das durch Herausbewegung eines Körpers aus dem uns bekannten Raume entstände. Unter dem viel mißbrauchten Ausdruck »sich vorstellen« oder »sich denken können, wie etwas geschieht« verstehe ich–und ich sehe nicht, wie man etwas anderes darunter verstehen kann, ohne allen Sinn des Ausdrucks aufzugeben–, daß man sich die Reihe der sinnlichen Eindrücke ausmalen könne, die man haben würde, wenn so etwas in einem einzelnen Falle vor sich ginge. Ist nun gar kein sinnlicher Eindruck bekannt, der sich auf einen solchen nie beobachteten Vorgang bezöge, wie für uns eine Bewegung nach einer vierten, für jene Flächenwesen eine Bewegung nach der uns bekannten dritten Dimension des Raumes wäre, so ist ein solches »Vorstellen« nicht möglich, ebenso wenig als ein von Jugend auf absolut Blinder sich wird die Farben »vorstellen« können, auch wenn man ihm eine begriffliche Beschreibung derselben geben könnte.

Jene Flächenwesen würden ferner auch kürzeste Linien in ihrem flächenhaften Raume ziehen können. Da wären nicht notwendig gerade Linien in unserem Sinne, sondern was wir nach geometrischer Terminologie geodätische Linien der Fläche, auf der jene leben, nennen würden, Linien, wie sie ein gespannter Faden beschreibt, den man an die Fläche anlegt, und der ungehindert an ihr gleiten kann. Ich will mir erlauben, im folgenden dergleichen Linien als die geradesten Linien der bezeichneten Fläche (beziehlich eines gegebenen Raumes) zu bezeichnen, um dadurch ihre Analogie mit der geraden Linie in der Ebene hervorzuheben. Ich hoffe den Begriff durch diesen Ausdruck der Anschauung meiner nicht mathematischen Zuhörer näherzurücken, ohne doch Verwechslungen zu veranlassen.

Wenn nun Wesen dieser Art auf einer unendlichen Ebene lebten, so würden sie genau dieselbe Geometrie aufstellen, welche in unserer Planimetrie enthalten ist. Sie würden behaupten, daß zwischen zwei Punkten nur eine gerade Linie möglich ist, daß durch einen dritten, außerhalb derselben liegenden Punkt nur eine Parallele mit der ersten geführt werden kann, daß übrigens gerade Linien in das Unendliche verlängert werden können, ohne daß ihre Enden sich wieder begegnen, und so weiter. Ihr Raum könnte unendlich ausgedehnt sein, aber auch, wenn sie an Grenzen ihrer Bewegung und Wahrnehmung stießen, würden sie sich eine Fortsetzung jenseits dieser Grenzen anschaulich vorstellen können. In dieser Vorstellung würde ihnen ihr Raum unendlich ausgedehnt erscheinen, gerade wie uns der unsrige, obgleich auch wir mit unserem Leib nicht unsere Erde verlassen können, und unser Blick nur so weit reicht, als sichtbare Fixsterne vorhanden sind.

Nun könnten aber intelligente Wesen dieser Art auch an der Oberfläche einer Kugel leben. Ihre kürzeste oder geradeste Linie zwischen zwei Punkten würde dann ein Bogen des größten Kreises sein, der durch die betreffenden Punkte zu legen ist. Jeder größte Kreis, der durch zwei gegebene Punkte geht, verfällt dabei in zwei Teile. Wenn beide ungleich lang sind, ist der kleinere Teil allerdings die einzige kürzeste Linie auf der Kugel, die zwischen diesen beiden Punkten besteht. Aber auch der andere größere Bogen desselben größten Kreises ist eine geodätische oder geradeste Linie, d. h. jedes kleinere Stück desselben ist eine kürzeste Linie zwischen seinen beiden Endpunkten. Wegen dieses Umstandes können wir den Begriff der geodätischen oder geradesten Linie nicht kurzweg mit dem der kürzesten Linie identifizieren. Wenn nun die beiden gegebenen Punkte Endpunkte desselben Durchmessers der Kugel sind, so schneiden alle durch diesen Durchmesser gelegten Ebenen Halbkreise aus der Kugelfläche, welche alle kürzeste Linien zwischen den beiden Endpunkten sind. In einem solchen Falle gibt es also unendlich viele untereinander gleiche kürzeste Linien zwischen den beiden gegebenen Punkten. Somit würde das Axiom, daß nur eine kürzeste Linie zwischen zwei Punkten bestehe, für die Kugelbewohner nicht ohne eine gewisse Ausnahme giltig sein.

Parallele Linien würden die Bewohner der Kugel gar nicht kennen. Sie würden behaupten, daß beliebige zwei geradeste Linien, gehörig verlängert, sich schließlich nicht nur in einem, sondern in zwei Punkten schneiden müßten. Die Summe der Winkel in einem Dreieck würde immer größer sein als zwei Rechte, und um so größer, je größer die Fläche des Dreiecks. Eben deshalb würde ihnen auch der Begriff der geometrischen Ähnlichkeit der Form zwischen größeren und kleineren Figuren derselben Art fehlen. Denn ein größeres Dreieck muß notwendig andere Winkel haben als ein kleineres. Ihr Raum würde allerdings unbegrenzt, aber endlich ausgedehnt gefunden oder mindestens vorgestellt werden müssen.

Es ist klar, daß die Wesen auf der Kugel bei denselben logischen Fähigkeiten, doch ein ganz anderes System geometrischer Axiome aufstellen müßten, als die Wesen auf der Ebene, und als wir selbst in unserem Raume von drei Dimensionen. Diese Beispiele zeigen uns schon, daß, je nach der Art des Wohnraumes, verschiedene geometrische Axiome aufgestellt werden müßten von Wesen, deren Verstandeskräfte den unsrigen ganz entsprechend sein könnten.

Aber gehen wir weiter. Denken wir uns vernünftige Wesen existierend an der Oberfläche eines eiförmigen Körpers. Zwischen je drei Punkten einer solchen Oberfläche könnte man kürzeste Linien ziehen und so ein Dreieck konstruieren. Wenn man aber versuchte an verschiedenen Stellen dieser Fläche kongruente Dreiecke zu konstruieren, so würde sich zeigen, daß, wenn zwei Dreiecke gleich lange Seiten haben, ihre Winkel nicht gleich groß ausfallen. An dem spitzeren Ende des Eies gezeichnet, würde die Winkelsumme des Dreiecks sich mehr von zwei Rechten unterscheiden, als wenn ein Dreieck mit denselben Seiten an dem stumpferen Ende gezeichnet würde; daraus geht hervor, daß an einer solchen Fläche sich nicht einmal ein so einfaches Raumgebilde, wie ein Dreieck, ohne Änderung seiner Form von einem Orte nach jedem anderen fortbewegen lassen würde. Ebenso würde sich zeigen, daß, wenn an verschiedenen Stellen einer solchen Oberfläche Kreise mit gleichen Radien konstruiert würden (die Länge der Radien immer durch kürzeste Linien längs der Fläche gemessen), deren Peripherie am stumpfen Ende größer ausfallen würde, als am spitzeren Ende.

Daraus folgt weiter, daß es eine besondere geometrische Eigenschaft einer Fläche ist, wenn sich in ihr liegende Figuren, ohne Veränderung ihrer sämtlichen längs der Fläche gemessenen Linien und Winkel, frei verschieben lassen, und daß dies nicht auf jeder Art von Fläche der Fall sein wird. Die Bedingung dafür, daß eine Fläche diese wichtige Eigenschaft habe, hatte schon Gauß in seiner berühmten Abhandlung über die Krümmung der Flächen nachgewiesen. Die Bedingung ist, daß das, was er das »Maß der Krümmung« genannt hat (nämlich der reziproke Wert des Produktes der beiden Hauptkrümmungsradien), überall längs der ganzen Ausdehnung der Fläche gleiche Größe habe.

Gauß hat gleichzeitig nachgewiesen, daß dieses Maß der Krümmung sich nicht verändert, wenn die Fläche gebogen wird, ohne dabei in irgendeinem Teil eine Dehnung oder Zusammenziehung zu erleiden. So können wir ein ebenes Papierblatt zu einem Zylinder oder einem Kegel (Düte) aufrollen, ohne daß die längs der Fläche des Blattes genommenen Abmessungen seiner Figuren sich verändern. Und ebenso können wir die halbkugelförmige geschlossene Hälfte einer Schweinsblase in Spindelform zusammenrollen, ohne die Abmessungen in dieser Fläche selbst zu verändern. Es wird also auch die Geometrie auf einer Ebene dieselbe sein wie in einer Zylinderfläche. Wir müssen uns nur im letzteren Falle vorstellen, daß unbegrenzt viele Lagen dieser Fläche, wie die Lagen eines umgewickelten Papierblattes, übereinander liegen, und daß man bei jedem ganzen Umgang um den Zylinderumfang in eine andere Lage hineinkommt, verschieden von derjenigen, in der man sich früher befand.

Diese Bemerkungen sind nötig, um Ihnen eine Vorstellung von einer Art von Fläche geben zu können, deren Geometrie der der Ebene im ganzen ähnlich ist, für welche aber das Axiom von den Parallellinien nicht gilt. Es ist dies eine Art gekrümmter Fläche, welche sich in geometrischer Beziehung wie das Gegenteil einer Kugel verhält, und die deshalb von dem ausgezeichneten italienischen Mathematiker E. Beltrami, der ihre Eigenschaften untersucht hat, die pseudosphärische Fläche genannt worden ist. Es ist eine sattelförmige Fläche, von der in unserem Raume nur begrenzte Stücke oder Streifen zusammenhängend dargestellt werden können, die man aber doch sich nach allen Richtungen in das Unendliche fortgesetzt denken kann, da man jedes an der Grenze des konstruierten Flächenteiles liegende Stück nach der Mitte desselben zurückgeschoben und dann fortgesetzt denken kann. Das verschobene Flächenstück muß dabei seine Biegung, aber nicht seine Dimensionen ändern, geradeso wie man auf einem durch tütenförmiges Zusammenrollen einer Ebene entstandenen Kegel ein Papierblatt hin und her schieben kann. Ein solches paßt sich der Kegelfläche überall an, aber es muß, näher der Spitze des Kegels, stärker gebogen werden und kann über die Spitze hinaus nicht so verschoben werden, daß es dem existierenden Kegel und seiner idealen Fortsetzung jenseits der Spitze angepaßt bliebe.

Wie die Ebene und die Kugel sind die pseudosphärischen Flächen von konstanter Krümmung, so daß sich jedes Stück derselben an jede andere Stelle der Fläche vollkommen anschließend anlegen kann, und also alle an einem Orte in der Fläche konstruierten Figuren an jeden anderen Ort in vollkommen kongruenter Form und mit vollkommener Gleichheit aller in der Fläche selbst liegenden Dimensionen übertragen werden können. Das von Gauß aufgestellte Maß der Krümmung, das für die Kugel positiv und für die Ebene gleich Null ist, würde für die pseudosphärischen Flächen einen konstanten, negativen Wert haben, weil die beiden Hauptkrümmungen einer sattelförmigen Fläche ihre Konkavität nach entgegengesetzten Seiten kehren.

Ein Streifen einer pseudosphärischen Fläche kann zum Beispiel aufgewickelt als Oberfläche eines Ringes dargestellt werden. Denken Sie sich eine Fläche wie aabb, Figur 1, um ihre Symmetrieaxe A B gedreht, so würden die beiden Bogen ab eine solche pseudosphärische Ringfläche beschreiben. Die beiden Ränder der Fläche oben bei aa und unten bei bb würden sich mit immer schärfer werdender Biegung nach außen wenden, bis die Fläche senkrecht zur Axe steht, und dort würde sie mit einer unendlich starken Krümmung an der Kante enden. Auch zu einem kelchförmigen Champagnerglase mit unendlich verlängertem, immer dünner werdendem Stiel wie Figur 2 könnte eine Hälfte einer pseudosphärischen Fläche aufgewickelt werden. Aber an einer Seite ist sie notwendig immer durch einen scharf abbrechenden Rand begrenzt, über den hinaus eine kontinuierliche Fortsetzung der Fläche nicht unmittelbar ausgeführt werden kann. Nur dadurch daß man jedes einzelne Stück des Randes losgeschnitten und längs der Fläche des Ringes oder Kelchglases verschoben denkt, kann man es zu Stellen von anderer Biegung bringen, an denen weitere Fortsetzung dieses Flächenstücks möglich ist.

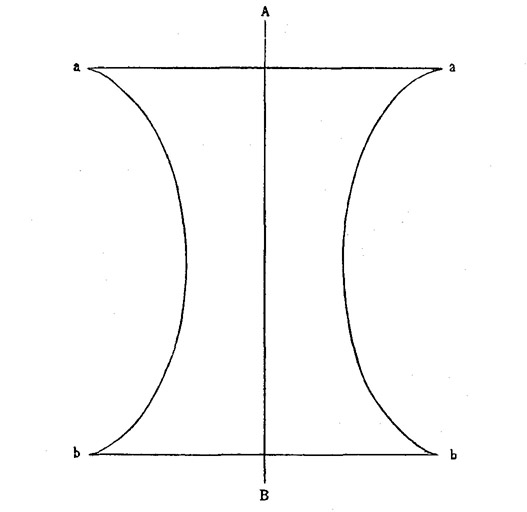
Fig. 1

In dieser Weise lassen sich denn auch die geradesten Linien der pseudosphärischen Fläche unendlich verlängern. Sie laufen nicht wie die der Kugel in sich zurück, sondern, wie auf der Ebene, ist zwischen zwei gegebenen Punkten immer nur eine einzige kürzeste Linie möglich. Aber das Axiom von den Parallelen trifft nicht zu. Wenn eine geradeste Linie auf der Fläche gegeben ist und ein Punkt außerhalb derselben, so läßt sich ein ganzes Bündel von geradesten Linien durch den Punkt legen, welche alle die erstgenannte Linie nicht schneiden, auch wenn sie ins Unendliche verlängert werden. Es sind dies alle Linien, welche zwischen zwei das Bündel begrenzenden geradesten Linien liegen. Die eine von diesen, unendlich verlängert, trifft die erstgenannte Linie im Unendlichen bei Verlängerung nach einer Seite, die andere bei Verlängerung nach der anderen Seite.

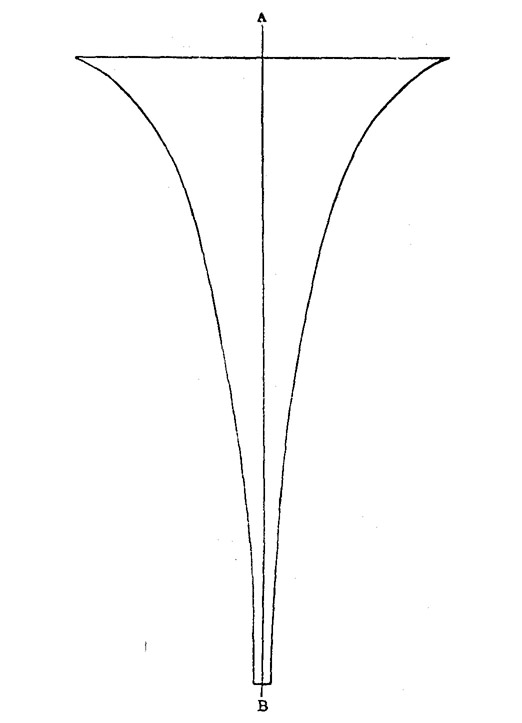
Fig. 2

Eine solche Geometrie, welche das Axiom von den Parallelen fallen läßt, ist übrigens schon im Jahre 1829 nach der synthetischen Methode des Euklid von dem Mathematiker N. I. Lobatschewsky zu Kasan vollständig ausgearbeitet worden. Es zeigte sich, daß deren System ebenso konsequent und ohne Widerspruch durchzuführen sei, wie das des Euklides. Diese Geometrie ist in vollständiger Übereinstimmung mit der der pseudosphärischen Flächen, wie sie Beltrami neuerdings ausgebildet hat.

Wir sehen daraus, daß in der Geometrie zweier Dimensionen die Voraussetzung, jede Figur könne, ohne irgendwelche Änderung ihrer in der Fläche liegenden Dimensionen, nach allen Richtungen hin fortbewegt werden, die betreffende Fläche charakterisiert als Ebene oder Kugel oder pseudosphärische Fläche. Das Axiom, daß zwischen je zwei Punkten immer nur eine kürzeste Linie bestehe, trennt die Ebene und pseudosphärische Fläche von der Kugel, und das Axiom von den Parallelen scheidet die Ebene von der Pseudosphäre. Diese drei Axiome sind also notwendig und hinreichend, um die Fläche, auf welche sich die Euklidische Planimetrie bezieht, als Ebene zu charakterisieren, im Gegensatz zu allen anderen Raumgebilden zweier Dimensionen.

Der Unterschied zwischen der Geometrie in der Ebene und derjenigen auf der Kugelfläche ist längst klar und anschaulich gewesen, aber der Sinn des Axioms von den Parallelen konnte erst verstanden werden, nachdem Gauß den Begriff der ohne Dehnung biegsamen Flächen und damit der möglichen unendlichen Fortsetzung der pseudosphärischen Flächen entwickelt hatte. Wir als Bewohner eines Raumes von drei Dimensionen und begabt mit Sinneswerkzeugen, um alle diese Dimensionen wahrzunehmen, können uns die verschiedenen Fälle, in denen flächenhafte Wesen ihre Raumanschauung auszubilden hätten, allerdings anschaulich vorstellen, weil wir zu diesem Ende nur unsere eigenen Anschauungen auf ein engeres Gebiet zu beschränken haben. Anschauungen, die man hat, sich wegdenken ist leicht; aber Anschauungen, für die man nie ein Analogon gehabt hat, sich sinnlich vorstellen ist sehr schwer. Wenn wir deshalb zum Raum von drei Dimensionen übergehen, so sind wir in unserem Vorstellungsvermögen gehemmt durch den Bau unserer Organe und die damit gewonnenen Erfahrungen, welche nur zu dem Raume passen, in dem wir leben.

Nun haben wir aber noch einen anderen Weg zur wissenschaftlichen Behandlung der Geometrie. Es sind nämlich alle uns bekannten Raumverhältnisse meßbar, das heißt, sie können auf Bestimmung von Größen (von Linienlängen, Winkeln, Flächen, Volumina) zurückgeführt werden. Eben deshalb können die Aufgaben der Geometrie auch dadurch gelöst werden, daß man die Rechnungsmethoden aufsucht, mittels deren man die unbekannten Raumgrößen aus den bekannten herzuleiten hat. Dies geschieht in der analytischen Geometrie, in welcher die sämtlichen Gebilde des Raumes nur als Größen behandelt und durch andere Größen bestimmt werden. Auch sprechen schon unsere Axiome von Raumgrößen. Die gerade Linie wird als die kürzeste zwischen zwei Punkten definiert, was eine Größenbestimmung ist. Das Axiom von den Parallelen sagt aus, daß, wenn zwei gerade Linien in derselben Ebene sich nicht schneiden (parallel sind), die Wechselwinkel, beziehlich die Gegenwinkel, an einer dritten, sie schneidenden, paarweise gleich sind. Oder dafür wird der Satz gesetzt, daß die Summe der Winkel in jedem Dreieck gleich zwei Rechten ist. Auch dies sind Größenbestimmungen.

Man kann also auch von dieser Seite des Raumbegriffs ausgehen, wonach die Lage jedes Punktes, in bezug auf irgendwelches als fest angesehenes Raumgebilde (Koordinatensystem), durch Messungen irgendwelcher Größen bestimmt werden kann; dann zusehen, welche besonderen Bestimmungen unserem Raum, wie er bei den tatsächlich auszuführenden Messungen sich darstellt, zukommen, und ob solche da sind, durch welche er sich von ähnlich mannigfaltig ausgedehnten Größen unterscheidet. Der der Wissenschaft leider zu früh entrissene Riemann in Göttingen hat zuerst diesen Weg eingeschlagen. Dieser Weg hat den eigentümlichen Vorzug, daß alle Operationen, die in ihm vorkommen, reine rechnende Größenbestimmungen sind, wobei die Gefahr, daß sich gewohnte Anschauungstatsachen als Denknotwendigkeiten unterschieben könnten, ganz wegfällt.

Die Zahl der Abmessungen, welche nötig ist, um die Lage eines Punktes zu geben, ist gleich der Anzahl der Dimensionen des betreffenden Raumes. In einer Linie genügt der Abstand von einem festen Punkte, also eine Größe; in einer Fläche muß man schon die Abstände von zwei festen Punkten angeben; im Raum von dreien, um die Lage des Punktes zu fixieren; oder wir brauchen, wie auf der Erde, geographische Länge, Breite und Hohe über dem Meere, oder, wie in der analytischen Geometrie gewöhnlich, die Abstände von drei Koordinatebenen. Riemann nennt ein System von Unterschieden, in welchem das Einzelne durch n-Abmessungen bestimmt werden kann, eine n-fach ausgedehnte Mannigfaltigkeit oder eine Mannigfaltigkeit von n-Dimensionen. Somit ist also der uns bekannte Raum, in dem wir leben, eine dreifach ausgedehnte Mannigfaltigkeit von Punkten, eine Fläche eine zweifache, eine Linie eine einfache, die Zeit ebenso eine einfache. Auch das System der Farben bildet eine dreifache Mannigfaltigkeit, insofern jede Farbe nach Thomas Youngs und Maxwells Untersuchungen dargestellt werden kann, als die Mischung dreier Grundfarben, von deren jeder ein bestimmtes Quantum anzuwenden ist. Mit dem Farbenkreisel kann man solche Mischungen und Abmessungen wirklich ausführen.

Ebenso könnten wir das Reich der einfachen Töne als eine Mannigfaltigkeit von zwei Dimensionen betrachten, wenn wir sie nur nach Tonhöhe und Tonstärke verschieden nehmen und die Verschiedenheiten der Klangfarbe beiseite lassen. Diese Verallgemeinerung des Begriffes ist sehr geeignet, um hervortreten zu lassen, wodurch sich der Raum von anderen Mannigfaltigkeiten dreier Dimensionen unterscheidet. Wir können, wie Sie alle aus alltäglicher Erfahrung wissen, im Raume den Abstand zweier übereinander gelegener Punkte vergleichen mit dem horizontalen Abstande zweier Punkte des Fußbodens, weil wir einen Maßstab bald an das eine, bald an das andere Paar anlegen können. Aber wir können nicht den Abstand zweier Töne von gleicher Höhe und verschiedener Intensität vergleichen mit dem zweier Töne von gleicher Intensität und verschiedener Höhe. Riemann zeigte durch Betrachtungen dieser Art, daß die wesentliche Grundlage jeder Geometrie der Ausdruck sei, durch welchen die Entfernung zweier in beliebiger Richtung von einander liegender, und zwar zunächst zweier unendlich wenig von einander entfernter Punkte gegeben wird. Für diesen Ausdruck nahm er aus der analytischen Geometrie die allgemeinste Form, welche derselbe erhält, wenn man die Art der Abmessungen, durch welche der Ort jedes Punktes gegeben wird, ganz beliebig läßt. Er zeigte dann, daß diejenige Art der Bewegungsfreiheit bei unveränderter Form, welche den Körpern in unserem Raum zukommt, nur bestehen kann, wenn gewisse, aus der Rechnung hervorgehende Größen, die bezogen auf die Verhältnisse an Flächen sich auf das Gaußsche Maß der Flächenkrümmung reduzieren, überall den gleichen Wert haben. Eben deshalb nennt Riemann diese Rechnungsgrößen, wenn sie für eine bestimmte Stelle nach allen Richtungen hin denselben Wert haben, das Krümmungsmaß des betreffenden Raumes an dieser Stelle. Um Mißverständnisse abzuwehren, will ich hier nur noch hervorheben, daß dieses sogenannte Krümmungsmaß des Raumes eine auf rein analytischem Wege gefundene Rechnungsgröße ist, und daß seine Einführung keineswegs auf einer Unterschiebung von Verhältnissen, die nur in der sinnlichen Anschauung Sinn hätten, beruht. Der Name ist nur als kurze Bezeichnung eines verwickelten Verhältnisses von dem einen Falle hergenommen, wo der bezeichneten Größe eine sinnliche Anschauung entspricht.

Wenn nun dieses Krümmungsmaß des Raumes überall den Wert Null hat, entspricht ein solcher Raum überall den Axiomen des Euklides. Wir können ihn in diesem Falle einen ebenen Raum nennen, im Gegensatz zu anderen analytisch konstruierbaren Räumen, die man gekrümmte nennen könnte, weil ihr Krümmungsmaß einen von Null verschiedenen Wert hat. Indessen läßt sich die analytische Geometrie für Räume der letzteren Art ebenso vollständig und in sich konsequent durchführen, wie die gewöhnliche Geometrie unseres tatsächlich bestehenden ebenen Raumes.

Ist das Krümmungsmaß positiv, so erhalten wir den sphärischen Raum, in welchem die geradesten Linien in sich zurücklaufen, und in welchem es keine Parallelen gibt. Ein solcher Raum wäre, wie die Oberfläche einer Kugel, unbegrenzt, aber nicht unendlich groß. Ein negatives konstantes Krümmungsmaß dagegen gibt den pseudosphärischen Raum, in welchem die geradesten Linien in das Unendliche auslaufen, und in jeder ebensten Fläche durch jeden Punkt ein Bündel von geradesten Linien zu legen ist, die eine gegebene andere geradeste Linie jener Fläche nicht schneiden.

Diese letzteren Verhältnisse hat Beltrami dadurch der Anschauung zugänglich gemacht, daß er zeigte, wie man die Punkte, Linien und Flächen eines pseudosphärischen Raumes von drei Dimensionen im Inneren einer Kugel des Euklidschen Raumes so abbilden kann, daß jede geradeste Linie des pseudosphärischen Raumes in der Kugel durch eine gerade Linie vertreten wird, jede ebenste Fläche des ersteren durch eine Ebene in der letzteren. Die Kugeloberfläche selbst entspricht dabei den unendlich entfernten Punkten des pseudosphärischen Raumes; die verschiedenen Teile desselben sind in ihrem Kugelabbild um so mehr verkleinert, je näher sie der Kugeloberfläche liegen und zwar in der Richtung der Kugelradien stärker als in den Richtungen senkrecht darauf. Gerade Linien in der Kugel, die sich erst außerhalb der Kugeloberfläche schneiden, entsprechen geradesten Linien des pseudosphärischen Raumes, die sich nirgends schneiden.

Somit zeigte sich, daß der Raum, als Gebiet meßbarer Größen betrachtet, keineswegs dem allgemeinsten Begriffe einer Mannigfaltigkeit von drei Dimensionen entspricht, sondern noch besondere Bestimmungen erhält, welche bedingt sind durch die vollkommen freie Beweglichkeit der festen Körper mit unveränderter Form nach allen Orten hin und bei allen möglichen Richtungsänderungen. Ferner durch den besonderen Wert des Krümmungsmaßes, welches für den tatsächlich vorliegenden Raum gleich Null zu setzen ist, oder sich wenigstens in seinem Werte nicht merklich von Null unterscheidet. Diese letztere Festsetzung ist in den Axiomen von den geraden Linien und von den Parallelen gegeben.

Während Riemann von den allgemeinsten Grundfragen der analytischen Geometrie her dieses neue Gebiet betrat, war ich selbst teils durch Untersuchungen über die räumliche Darstellung des Systems der Farben, also durch Vergleichung einer dreifach ausgedehnten Mannigfaltigkeit mit einer anderen, teils durch Untersuchungen über den Ursprung unseres Augenmaßes für Abmessungen des Gesichtsfeldes zu ähnlichen Betrachtungen gekommen. Riemann ging von dem oben erwähnten algebraischen Ausdrucke, welcher die Entfernungen zweier einander unendlich naher Punkte in allgemeinster Form darstellt, als seiner Grundannahme aus, und leitete daraus die Sätze über Beweglichkeit fester Raumgebilde her; während ich von der Tatsache der Beobachtung ausgegangen bin, daß in unserem Raum die Bewegung fester Raumgebilde mit demjenigen Grade von Freiheit möglich ist, den wir kennen, und aus dieser Tatsache die Notwendigkeit jenes algebraischen Ausdrucks hergeleitet habe, den Riemann als Axiom hinstellt. Die Annahme, welche ich der Rechnung zugrunde legen mußte, waren die folgenden.

Erstens–um überhaupt rechnende Behandlung möglich zu machen–muß vorausgesetzt werden, daß die Lage jedes Punktes A gegen gewisse als unverständlich und fest betrachtete Raumgebilde durch Messungen von irgendwelchen Raumgrößen, seien es Linien, oder Winkel zwischen Linien, oder Winkel zwischen Flächen usw. bestimmt werden könne. Bekanntlich nennt man die zur Bestimmung der Lage des Punktes A nötigen Abmessungen seine Koordinaten. Die Anzahl der im allgemeinen zur vollständigen Bestimmung der Lage eines jeden Punktes nötigen Koordinaten bestimmt die Anzahl der Dimensionen des betreffenden Raumes. Es wird vorausgesetzt, daß bei Bewegung des Punktes A sich die als Koordinaten gebrauchten Raumgrößen kontinuierlich verändern.

Zweitens ist die Definition eines festen Körpers, beziehlich festen Punktsystems zu geben, wie sie nötig ist, um Vergleichung von Raumgrößen durch Kongruenz vornehmen zu können. Da wir hier noch keine speziellen Methoden zur Messung der Raumgrößen voraussetzen dürfen, so kann die Definition eines festen Körpers nur erst durch folgendes Merkmal gegeben werden: Zwischen den Koordinaten je zweier Punkte, die einem festen Körper angehören, muß eine Gleichung bestehen, die eine bei jeder Bewegung des Körpers unveränderte Raumbeziehung zwischen den beiden Punkten (welche sich schließlich als ihre Entfernung ergibt) ausspricht, und welche für kongruente Punktpaare die gleiche ist. Kongruent aber sind solche Punktpaare, die nach einander mit demselben im Raume festen Punktpaare zusammenfallen können.

Trotz ihrer anscheinend so unbestimmten Fassung ist diese Bestimmung äußerst folgenreich, weil bei Vermehrung der Punktzahl die Anzahl der Gleichungen viel schneller wächst, als die Zahl der durch sie bestimmten Koordinaten der Punkte. Fünf Punkte, A, B, C, D, E, geben zehn verschiedene Punktpaare:

also zehn Gleichungen, die im Raum von drei Dimensionen fünfzehn veränderliche Koordinaten enthalten, von denen aber sechs frei verfügbar bleiben müssen, wenn das System der fünf Punkte frei beweglich und drehbar sein soll. Es dürfen also durch jene zehn Gleichungen nur neun Koordinaten bestimmt werden, als abhängig von jenen sechs veränderlichen. Bei sechs Punkten bekommen wir fünfzehn Gleichungen für zwölf veränderliche Größen, bei sieben Punkten einundzwanzig Gleichungen für fünfzehn Größen usw. Nun können wir aber aus n von einander unabhängigen Gleichungen n darin vorkommende Größen bestimmen. Haben wir mehr als n Gleichungen, so müssen die überzähligen selbst herzuleiten sein aus den n ersten derselben. Daraus folgt, daß jene Gleichungen, welche zwischen den Koordinaten jedes Punktpaares eines festen Körpers bestehen, von besonderer Art sein müssen; so daß, wenn sie im Raum von drei Dimensionen für neun aus je fünf Punkten gebildete Punktpaare erfüllt sind, aus ihnen die Gleichung für das zehnte Paar identisch folgt. Auf diesem Umstande beruht es, daß die genannte Annahme für die Definition der Festigkeit doch genügt, um die Art der Gleichungen zu bestimmen, welche zwischen den Koordinaten zweier fest mit einander verbundener Punkte bestehen.

Drittens ergab sich, daß der Rechnung noch eine besondere Eigentümlichkeit der Bewegung fester Körper als Tatsache zugrunde gelegt werden mußte, eine Eigentümlichkeit, welche uns so geläufig ist, daß wir ohne diese Untersuchung vielleicht nie darauf verfallen wären, sie als etwas zu betrachten, was auch nicht sein könnte. Wenn wir nämlich in unserem Raum von drei Dimensionen zwei Punkte eines festen Körpers festhalten, so kann er nur noch Drehungen um deren gerade Verbindungslinie als Drehachse machen. Drehen wir ihn einmal ganz um, so kommt er genau wieder in die Lage, in der er sich zuerst befunden hatte. Daß nun Drehung ohne Umkehr jeden festen Körper immer wieder in seine Anfangslage zurückführt, muß besonders erwähnt werden. Es wäre eine Geometrie möglich, wo dies nicht so wäre. Am einfachsten ist dies für die Geometrie der Ebene einzusehen. Man denke sich, daß bei jeder Drehung jeder ebenen Figur ihre linearen Dimensionen dem Drehungswinkel proportional wüchsen, so würde nach einer ganzen Drehung um dreihundertsechzig Grad die Figur nicht mehr ihrem Anfangszustande kongruent sein. Übrigens würde ihr aber jede zweite Figur, die ihr in der Anfangslage kongruent war, auch in der zweiten Lage kongruent gemacht werden können, wenn auch die zweite Figur um dreihundertsechzig Grad gedreht wird. Es würde ein konsequentes System der Geometrie auch unter dieser Annahme möglich sein, welches nicht unter die Riemannsche Form fällt.

Andererseits habe ich gezeigt, daß die aufgezählten drei Annahmen zusammengenommen ausreichend sind, um den von Riemann angenommenen Ausgangspunkt der Untersuchung zu begründen, und damit auch alle weiteren Ergebnisse von dessen Arbeit, die sich auf den Unterschied der verschiedenen Räume nach ihrem Krümmungsmaß beziehen.

Es ließe sich nun noch fragen, ob auch die Gesetze der Bewegung und ihrer Abhängigkeit von den bewegenden Kräften ohne Widerspruch auf die sphärischen oder pseudosphärischen Räume übertragen werden können. Diese Untersuchung ist von Herrn Lipschitz in Bonn durchgeführt worden. Es läßt sich in der Tat der zusammenfassende Ausdruck aller Gesetze der Dynamik, das Hamiltonsche Prinzip, direkt auf Räume, deren Krümmungsmaß nicht gleich Null ist, übertragen. Also auch nach dieser Seite hin verfallen die abweichenden Systeme der Geometrie in keinen Widerspruch.

Wir werden nun weiter zu fragen haben, wo diese besonderen Bestimmungen herkommen, welche unsern Raum als ebenen Raum charakterisieren, da dieselben, wie sich gezeigt hat, nicht in dem allgemeinen Begriff einer ausgedehnten Größe von drei Dimensionen und freier Beweglichkeit der in ihr enthaltenen begrenzten Gebilde eingeschlossen sind. Denknotwendigkeiten, die aus dem Begriff einer solchen Mannigfaltigkeit und ihrer Meßbarkeit, oder aus dem allgemeinsten Begriff eines festen in ihr enthaltenen Gebildes und seiner freiesten Beweglichkeit herfließen, sind sie nicht.

Wir wollen nun die entgegengesetzte Annahme, die sich über ihren Ursprung machen läßt, untersuchen, die Frage nämlich, ob sie empirischen Ursprungs seien, ob sie aus Erfahrungstatsachen abzuleiten, durch solche zu erweisen, beziehlich zu prüfen und vielleicht auch zu widerlegen seien. Diese letztere Eventualität würde dann auch einschließen, daß wir uns Reihen beobachtbarer Erfahrungstatsachen müßten vorstellen können, durch welche ein anderer Wert des Krümmungsmaßes angezeigt würde, als derjenige ist, den der ebene Raum des Euklides hat. Wenn aber Räume anderer Art in dem angegebenen Sinne vorstellbar sind, so wäre damit auch widerlegt, daß die Axiome der Geometrie notwendige Folgen einer a priori gegebenen transzendentalen Form unserer Anschauungen im Kantschen Sinne seien.

Der Unterschied der Euklidschen, sphärischen und pseudosphärischen Geometrie beruht, wie oben bemerkt, auf dem Wert einer gewissen Konstante, welche Riemann das Krümmungsmaß des betreffenden Raumes nennt, und deren Wert gleich Null sein muß, wenn die Axiome des Euklides gelten. Ist sie nicht gleich Null, so würden Dreiecke von großem Flächeninhalt eine andere Winkelsumme haben müssen, als kleine, erstere im sphärischen Raum eine größere, im pseudosphärischen eine kleinere. Ferner ist geometrische Ähnlichkeit großer und kleiner Körper oder Figuren nur möglich im Euklidschen Raum. Alle Systeme praktisch ausgeführter geometrischer Messungen, bei denen die drei Winkel großer geradliniger Dreiecke einzeln gemessen worden sind, also auch namentlich alle Systeme astronomischer Messungen, welche die Parallaxe der unmeßbar weit entfernten Fixsterne gleich Null ergeben (im pseudosphärischen Raum müßten auch die unendlich entfernten Punkte positive Parallaxe haben), bestätigen empirisch das Axiom von den Parallelen, und zeigen, daß in unserem Raume und bei Anwendung unserer Messungsmethoden das Krümmungsmaß des Raumes als von Null ununterscheidbar erscheint. Freilich muß mit Riemann die Frage aufgeworfen werden, ob sich dies nicht vielleicht anders verhalten würde, wenn wir statt unserer begrenzten Standlinien, deren größte die große Achse der Erdbahn ist, größere Standlinien benutzen könnten.

Aber wir dürfen dabei nicht vergessen, daß alle geometrischen Messungen schließlich auf dem Prinzip der Kongruenz beruhen. Wir messen Entfernungen von Punkten, indem wir den Zirkel oder den Maßstab oder die Meßkette zu ihnen hinbewegen. Wir messen Winkel, indem wir den geteilten Kreis oder den Theodoliten an den Scheitel des Winkels bringen. Daneben bestimmen wir gerade Linien auch durch den unserer Erfahrung nach geradlinigen Gang der Lichtstrahlen; aber daß das Licht sich längs kürzester Linien ausbreitet, so lange es in einem ungeänderten brechenden Medium bleibt, würde sich ebenso auch auf Räume von anderem Krümmungsmaß übertragen lassen. Alle unsere geometrischen Messungen beruhen also auf der Voraussetzung, daß unsere von uns für fest gehaltenen Meßwerkzeuge wirklich Körper von unveränderlicher Form sind, oder daß sie wenigstens keine anderen Arten von Formveränderung erleiden, als diejenigen, die wir an ihnen kennen, wie z. B. die von geänderter Temperatur, oder die kleinen Dehnungen, welche von der bei geänderter Stellung anders wirkenden Schwere herrühren.

Wenn wir messen, so führen wir nur mit den besten und zuverlässigsten uns bekannten Hilfsmitteln dasselbe aus, was wir sonst durch Beobachtung nach dem Augenmaß und dem Tastsinn, oder durch Abschreiten zu ermitteln pflegen. In den letzteren Fällen ist unser eigener Körper mit seinen Organen das Meßwerkzeug, welches wir im Raum herumtragen. Bald ist die Hand, bald sind die Beine unser Zirkel, oder das nach allen Richtungen sich wendende Auge, der Theodolit, mit dem wir Bogenlängen oder Flächenwinkel im Gesichtsfelde abmessen.

Jede Größe vergleichende Schätzung oder Messung räumlicher Verhältnisse geht also aus von einer Voraussetzung über das physikalische Verhalten gewisser Naturkörper, sei es unseres eigenen Leibes, sei es der angewendeten Meßinstrumente, welche Voraussetzung übrigens den höchsten Grad von Wahrscheinlichkeit haben und mit allen uns sonst bekannten physikalischen Verhältnissen in der besten Übereinstimmung stehen mag, aber jedenfalls über das Gebiet der reinen Raumanschauungen hinausgreift.

Ja, es läßt sich ein bestimmtes Verhalten der uns als fest erscheinenden Körper angeben, bei welchem die Messungen im Euklidschen Raume so ausfallen würden, als wären sie im pseudosphärischen oder sphärischen Raum angestellt. Um dies einzusehen, erinnere ich zunächst daran, daß, wenn die sämtlichen linearen Dimensionen der uns umgebenden Körper und die unseres eigenen Leibes mit ihnen in gleichem Verhältnisse, z. B. alle auf die Hälfte verkleinert oder alle auf das Doppelte vergrößert würden, wir eine solche Änderung durch unsere Mittel der Raumanschauung gar nicht würden bemerken können. Dasselbe würde aber auch der Fall sein, wenn die Dehnung oder Zusammenziehung nach verschiedenen Richtungen hin verschieden wäre, vorausgesetzt, daß unser eigener Leib in derselben Weise sich veränderte und vorausgesetzt ferner, daß ein Körper, der sich drehte, in jedem Augenblick ohne mechanischen Widerstand zu erleiden oder auszuüben, denjenigen Grad der Drehung seiner verschiedenen Dimensionen annehme, der seiner zeitigen Lage entspricht. Man denke an das Abbild der Welt in einem Konvexspiegel. Die bekannten versilberten Kugeln, welche in Gärten aufgestellt zu werden pflegen, zeigen die wesentlichen Erscheinungen eines solchen Bildes, wenn auch gestört durch einige optische Unregelmäßigkeiten. Ein gut gearbeiteter Konvexspiegel von nicht zu großer Öffnung zeigt das Spiegelbild jedes vor ihm liegenden Gegenstandes scheinbar körperlich und in bestimmter Lage und Entfernung hinter seiner Fläche. Aber die Bilder des fernen Horizontes und der Sonne am Himmel liegen in begrenzter Entfernung, welche der Brennweite des Spiegels gleich ist, hinter dem Spiegel. Zwischen diesen Bildern und der Oberfläche des Spiegels sind die Bilder aller anderen vor letzterem liegenden Objekte enthalten, aber so, daß die Bilder um so mehr verkleinert und um so mehr abgeplattet sind, je ferner ihre Objekte vom Spiegel liegen. Die Abplattung, das heißt die Verkleinerung der Tiefendimensionen, ist verhältnismäßig bedeutender als die Verkleinerung der Flächendimensionen. Dennoch wird jede gerade Linie der Außenwelt durch eine gerade Linie im Bilde, jede Ebene durch eine Ebene dargestellt. Das Bild eines Mannes, der mit einem Maßstab eine von dem Spiegel sich entfernende gerade Linie abmißt, würde immer mehr zusammenschrumpfen, je mehr das Original sich entfernt, aber mit seinem ebenfalls zusammenschrumpfenden Maßstab würde der Mann im Bild genau dieselbe Zahl von Zentimetern herauszählen, wie der Mann in der Wirklichkeit; überhaupt würden alle geometrischen Messungen von Linien oder Winkeln, mit den gesetzmäßig veränderlichen Spiegelbildern der wirklichen Instrumente ausgeführt, genau dieselben Resultate ergeben wie die in der Außenwelt. Alle Kongruenzen würden in den Bildern bei wirklicher Aneinanderlagerung der betreffenden Körper ebenso passen wie in der Außenwelt, alle Visierlinien der Außenwelt durch gerade Visierlinien im Spiegel ersetzt sein. Kurz, ich sehe nicht, wie die Männer im Spiegel herausbringen sollten, daß ihre Körper nicht feste Körper und ihre Erfahrungen gute Beispiele für die Richtigkeit der Axiome des Euklides seien. Könnten sie aber hinausschauen in unsere Welt, wie wir hineinschauen in die ihrige, ohne die Grenze überschreiten zu können, so würden sie unsere Welt für das Bild eines Konvexspiegels erklären müssen und von uns gerade so reden, wie wir von ihnen, und wenn sich die Männer beider Welten mit einander besprechen könnten, so würde, soweit ich sehe, keiner den anderen überzeugen können, daß er die wahren Verhältnisse habe, der andere die verzerrten; ja ich kann nicht erkennen, daß eine solche Frage überhaupt einen Sinn hätte, so lange wir keine mechanischen Betrachtungen einmischen.

Nun ist Beltramis Abbildung des pseudosphärischen Raumes in einer Vollkugel des Euklidschen Raumes von ganz ähnlicher Art, nur daß die Fläche des Hintergrundes nicht eine Ebene, wie bei dem Konvexspiegel, sondern eine Kugelfläche ist, und das Verhältnis, in welchem sich die der Kugelfläche näher kommenden Bilder zusammenziehen, einen anderen mathematischen Ausdruck hat. Denkt man sich also umgekehrt, daß in der Kugel, für deren Innenraum die Axiome des Euklides gelten, sich Körper bewegen, die, wenn sie sich vom Mittelpunkt entfernen, sich jedesmal zusammenziehen, ähnlich den Bildern im Konvexspiegel, und zwar sich in der Weise zusammenziehen, daß ihre im pseudosphärischen Raum konstruierten Abbilder unveränderte Dimensionen behalten, so würden Beobachter, deren Leiber selbst dieser Veränderung regelmäßig unterworfen wären, bei geometrischen Messungen, wie sie sie ausführen könnten, Ergebnisse erhalten, als lebten sie selbst im pseudosphärischen Raum.

Wir können von hier aus sogar noch einen Schritt weiter gehen; wir können daraus ableiten, wie einem Beobachter, dessen Augenmaß und Raumerfahrung sich gleich den unserigen im ebenen Raum ausgebildet haben, die Gegenstände einer pseudosphärischen Welt erscheinen würden, falls er in eine solche eintreten könnte. Ein solcher Beobachter würde die Linien der Lichtstrahlen oder die Visierlinien seines Auges fortfahren als gerade Linien anzusehen, wie solche im ebenen Raum vorkommen, und wie sie in dem kugeligen Abbild des pseudosphärischen Raumes wirklich sind. Das Gesichtsfeld der Objekte im pseudosphärischen Raum würde ihm deshalb denselben Eindruck machen, als befände er sich im Mittelpunkt des Beltramischen Kugelbildes. Er würde die entferntesten Gegenstände dieses Raumes in endlicher Entfernung rings um sich zu erblicken glauben, nehmen wir beispielsweise an, in hundert Fuß Abstand. Ginge er aber auf diese entfernten Gegenstände zu, so würden sie sich vor ihm dehnen, und zwar noch mehr nach der Tiefe, als nach der Fläche; hinter ihm aber würden sie sich zusammenziehen. Er würde erkennen, daß er nach dem Augenmaß falsch geurteilt hat. Sähe er zwei gerade Linien, die sich nach seiner Schätzung mit einander parallel bis auf diese Entfernung von hundert Fuß, wo ihm die Welt abgeschlossen erscheint, hinausziehen, so würde er, ihnen nachgehend, erkennen, daß sie bei dieser Dehnung der Gegenstände, denen er sich nähert, auseinander rücken, je mehr er an ihnen vorschreitet; hinter ihm dagegen würde ihr Abstand zu schwinden scheinen, so daß sie ihm beim Vorschreiten immer mehr divergent und immer entfernter von einander erscheinen würden. Zwei gerade Linien aber, die vom ersten Standpunkt aus nach einem und demselben Punkt des Hintergrundes in hundert Fuß Entfernung zu konvergieren scheinen, würden dies immer tun, so weit er ginge und er würde ihren Schnittpunkt nie erreichen. Nun können wir ganz ähnliche Bilder unserer wirklichen Welt erhalten, wenn wir eine große Konvexlinse von entsprechender negativer Brennweite vor die Augen nehmen, oder auch nur zwei konvexe Brillengläser, die etwas prismatisch geschliffen sein müßten, als wären sie Stücke aus einer zusammenhängenden größeren Linse. Solche zeigen uns ebenso, wie die oben erwähnten Konvexspiegel, die fernen Gegenstände genähert, die fernsten bis zur Entfernung des Brennpunktes der Linse. Wenn wir uns mit einer solchen Linse vor den Augen bewegen, gehen ganz ähnliche Dehnungen der Gegenstände, auf die wir zugehen, vor, wie ich sie für den pseudosphärischen Raum beschrieben habe. Wenn nun jemand eine solche Linse vor die Augen nimmt, nicht einmal eine Linse von hundert Fuß, sondern eine viel stärkere von nur sechzig Zoll Brennweite, so merkt er im ersten Augenblick vielleicht, daß er die Gegenstände genähert sieht. Aber nach wenigem Hin- und Hergehen schwindet die Täuschung, und er beurteilt trotz der falschen Bilder die Entfernung richtig. Wir haben allen Grund zu vermuten, daß es uns im pseudosphärischen Raum bald genug ebenso gehen würde, wie es bei einem angehenden Brillenträger nach wenigen Stunden schon der Fall ist. Kurz der pseudosphärische Raum würde uns verhältnismäßig gar nicht sehr fremdartig erscheinen; wir würden uns nur in der ersten Zeit, bei der Abmessung der Größe und Entfernung fernerer Gegenstände nach ihrem Gesichtseindruck, Täuschungen unterworfen finden.

Die entgegengesetzten Täuschungen würde ein sphärischer Raum von drei Dimensionen mit sich bringen, wenn wir mit dem im Euklidschen Raume erworbenen Augenmaße in ihn eintreten. Wir würden entferntere Gegenstände für entfernter und größer halten, als sie sind; wir würden auf sie zugehend finden, daß wir sie schneller erreichen, als wir nach dem Gesichtsbild annehmen mußten. Wir würden aber auch Gegenstände vor uns sehen, die wir nur mit divergierenden Gesichtslinien fixieren können; dies würde bei allen denjenigen der Fall sein, welche von uns weiter als ein Quadrant eines größten Kreises entfernt sind. Diese Art des Anblicks würde uns kaum sehr ungewöhnlich vorkommen, denn wir können denselben auch für irdische Gegenstände hervorbringen, wenn wir vor das eine Auge ein schwach prismatisches Glas nehmen, dessen dickere Seite zur Nase gekehrt ist. Auch dann müssen wir die Augen divergent stellen, um entfernte Gegenstände zu fixieren. Das erregt ein gewisses Gefühl ungewohnter Anstrengung in den Augen, ändert aber nicht merklich den Anblick der so gesehenen Gegenstände. Den seltsamsten Teil des Anblicks der sphärischen Welt würde aber unser eigener Hinterkopf bilden, in dem alle unsere Gesichtslinien wieder zusammenlaufen würden, so weit sie zwischen anderen Gegenständen frei durchgehen könnten, und welcher den äußersten Hintergrund des ganzen perspektivischen Bildes ausfüllen müßte.

Dabei ist freilich noch weiter zu bemerken, daß, wie eine kleine ebene elastische Scheibe, etwa eine kleine ebene Kautschukplatte, einer schwach gewölbten Kugelfläche nur unter relativer Kontraktion ihres Randes und Dehnung ihrer Mitte angepaßt werden kann, so auch unser im Euklidschen ebenen Raum gewachsener Körper nicht in einen gekrümmten Raum übergehen könnte ohne ähnliche Dehnungen und Zusammenpressungen seiner Teile zu erleiden, deren Zusammenhang natürlich nur so weit erhalten bleiben könnte, als die Elastizität der Teile ein Nachgeben ohne Reißen und Brechen erlaubte. Die Art der Dehnung würde dieselbe sein müssen, als wenn wir uns im Mittelpunkt von Beltramis Kugel einen kleinen Körper dächten, und von diesem dann auf sein pseudosphärisches oder sphärisches Abbild übergingen. Damit ein solcher Übergang als möglich erscheine, wird immer vorausgesetzt werden müssen, daß der übergehende Körper hinreichend elastisch und klein sei im Vergleich mit dem reellen oder imaginären Krümmungsradius des gekrümmten Raumes, in den er übergehen soll.

Es wird dies genügen um zu zeigen, wie man auf dem eingeschlagenen Weg aus den bekannten Gesetzen unserer sinnlichen Wahrnehmungen die Reihe der sinnlichen Eindrücke herleiten kann, welche eine sphärische oder pseudosphärische Welt uns geben würde, wenn sie existierte. Auch dabei treffen wir nirgends auf eine Unfolgerichtigkeit oder Unmöglichkeit, ebensowenig wie in der rechnenden Behandlung der Maßverhältnisse. Wir können uns den Anblick einer pseudosphärischen Welt ebensogut nach allen Richtungen hin ausmalen, wie wir ihren Begriff entwickeln können. Wir können deshalb auch nicht zugeben, daß die Axiome unserer Geometrie in der gegebenen Form unseres Anschauungsvermögens begründet wären, oder mit einer solchen irgendwie zusammenhingen.

Anders ist es mit den drei Dimensionen des Raumes. Da alle unsere Mittel sinnlicher Anschauung sich nur auf einen Raum von drei Dimensionen erstrecken, und die vierte Dimension nicht bloß eine Abänderung von vorhandenem, sondern etwas vollkommen Neues wäre, so befinden wir uns schon wegen unserer körperlichen Organisation in der absoluten Unmöglichkeit, uns eine Anschauungsweise einer vierten Dimension vorzustellen.

Schließlich möchte ich nun noch hervorheben, daß die geometrischen Axiome gar nicht Sätze sind, die nur der reinen Raumlehre angehörten. Sie sprechen, wie ich schon erwähnt habe, von Größen. Von Größen kann man nur reden, wenn man irgend welches Verfahren kennt und im Sinn hat, nach dem man diese Größen vergleichen, in Teile zerlegen und messen kann. Alle Raummessung, und daher überhaupt alle auf den Raum angewendeten Größenbegriffe setzen also die Möglichkeit der Bewegung von Raumgebilden voraus, deren Form und Größe man trotz der Bewegung für unveränderlich halten darf. Solche Raumformen pflegt man in der Geometrie allerdings nur als geometrische Körper, Flächen, Winkel, Linien zu bezeichnen, weil man von allen anderen Unterschieden physikalischer und chemischer Art, welche die Naturkörper zeigen, abstrahiert; aber man bewahrt doch die eine physikalische Eigenschaft derselben, die Festigkeit. Für die Festigkeit der Körper und Raumgebilde haben wir aber kein anderes Merkmal, als daß sie, zu jeder Zeit und an jedem Ort und nach jeder Drehung aneinander gelegt, immer wieder dieselben Kongruenzen zeigen, wie vorher. Ob sich aber die aneinander gelegten Körper nicht selbst beide in gleichem Sinne verändert haben, können wir auf rein geometrischem Wege, ohne mechanische Betrachtungen hinzuzunehmen, gar nicht entscheiden.

Wenn wir es zu irgendeinem Zwecke nützlich fänden, so könnten wir in vollkommen folgerichtiger Weise den Raum, in welchem wir leben, als den scheinbaren Raum hinter einem Konvexspiegel mit verkürztem und zusammengezogenem Hintergrunde betrachten; oder wir könnten eine abgegrenzte Kugel unseres Raumes, jenseits deren Grenzen wir nichts mehr wahrnehmen, als den unendlichen pseudosphärischen Raum betrachten. Wir müßten dann nur den Körpern, welche uns als fest erscheinen, und ebenso unserem eigenen Leibe gleichzeitig die entsprechenden Dehnungen und Verkürzungen zuschreiben, und würden allerdings das System unserer mechanischen Prinzipien gleichzeitig gänzlich verändern müssen; denn schon der Satz, daß jeder bewegte Punkt, auf den keine Kraft wirkt, sich in gerader Linie mit unveränderter Geschwindigkeit fortbewegt, paßt auf das Abbild der Welt im Konvexspiegel nicht mehr. Die Bahnlinie wäre zwar noch gerade, aber die Geschwindigkeit abhängig vom Ort.

Die geometrischen Axiome sprechen also gar nicht über Verhältnisse des Raumes allein, sondern gleichzeitig auch über das mechanische Verhalten unserer festesten Körper bei Bewegungen. Man könnte freilich auch den Begriff des festen geometrischen Raumgebildes als einen transzendentalen Begriff auffassen, der unabhängig von wirklichen Erfahrungen gebildet wäre, und dem diese nicht notwendig zu entsprechen brauchten, wie ja unsere Naturkörper tatsächlich ganz rein und ungestört nicht einmal denjenigen Begriffen entsprechen, die wir auf dem Wege der Induktion von ihnen abstrahiert haben. Unter Hinzunahme eines solchen nur als Ideal konzipierten Begriffs der Festigkeit könnte dann ein strenger Kantianer allerdings die geometrischen Axiome als a priori durch transzendentale Anschauung gegebene Sätze betrachten, die durch keine Erfahrung bestätigt oder widerlegt werden könnten, weil man erst nach ihnen zu entscheiden hätte, ob irgend welche Naturkörper als feste Körper zu betrachten seien. Dann müßten wir aber behaupten, daß unter dieser Auffassung die geometrischen Axiome gar keine synthetischen Sätze im Sinne Kants wären. Denn sie würden dann nur etwas aussagen, was aus dem Begriff der zur Messung notwendigen festen geometrischen Gebilde analytisch folgen würde, da als feste Gebilde nur solche anerkannt werden könnten, die jenen Axiomen genügen.

Nehmen wir aber zu den geometrischen Axiomen noch Sätze hinzu, die sich auf die mechanischen Eigenschaften der Naturkörper beziehen, wenn auch nur den Satz von der Trägheit, oder den Satz, daß die mechanischen und physikalischen Eigenschaften der Körper unter übrigens gleichbleibenden Einflüssen nicht vom Ort, wo sie sich befinden, abhängen können, dann erhält ein solches System von Sätzen einen wirklichen Inhalt, der durch Erfahrung bestätigt oder widerlegt werden, eben deshalb aber auch durch Erfahrung gewonnen werden kann.

Übrigens ist es natürlich nicht meine Absicht, zu behaupten, daß die Menschheit erst durch sorgfältig ausgeführte Systeme genauer geometrischer Messungen Anschauungen des Raumes, die den Axiomen des Euklides entsprechen, gewonnen habe. Es mußte vielmehr eine Reihe alltäglicher Erfahrungen, namentlich die Anschauung von der geometrischen Ähnlichkeit großer und kleiner Körper, welche nur im ebenen Raum möglich ist, darauf führen, jede geometrische Anschauung, die dieser Tatsache widersprach, als unmöglich zu verwerfen. Dazu war keine Erkenntnis des begrifflichen Zusammenhanges zwischen der beobachteten Tatsache geometrischer Ähnlichkeit und den Axiomen nötig, sondern nur durch zahlreiche und genaue Beobachtungen von Raumverhältnisse gewonnene anschauliche Kenntnis ihres typischen Verhaltens; eine solche Art der Anschauung, wie sie der Künstler von den darzustellenden Gegenständen besitzt und mittels deren er sicher und fein entscheidet, ob eine versuchte neue Kombination der Natur des darzustellenden Gegenstandes entspricht oder nicht. Das wissen wir zwar in unserer Sprache auch mit keinem anderen Namen als dem der »Anschauung« zu bezeichnen; aber es ist dies eine empirische, durch Häufung und Verstärkung gleichartig wiederkehrender Eindrücke, in unserem Gedächtnis gewonnene Kenntnis, keine transzendentale und vor aller Erfahrung gegebene Anschauungsform. Daß dergleichen empirisch erlangte und noch nicht zur Klarheit des bestimmt ausgesprochenen Begriffs durchgearbeitete Anschauungen eines typischen gesetzlichen Verhaltens häufig genug den Metaphysikern als a priori gegebene Sätze imponiert haben, brauche ich hier nicht weiter zu erörtern.