
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Ich nahm an, daß 2 097 152 Sätze sich in 1 048 576 rote und ebensoviel schwarze teilten. Es besteht ja kein Grund für das Gegenteil. Das wäre mit dem Prinzip der simple chance im Widerspruch. Wenn nun auch einmal eine der beiden Farben vorherrscht, so kommt doch immer ein Augenblick von Gleichheit heraus. Wollte man das bestreiten, so müßte man annehmen, daß entweder die Farbe, die gerade voraus ist, stets den Vorrang behaupten wird – was gegen den gleichen Anspruch der anderen Farbe streitet – oder daß die Farben, nachdem einmal eine vorausgeeilt ist, von nun an immer eine gleiche Häufigkeit haben würden – wodurch ein einmal bestehender Unterschied konsolidiert würde. Das ist aber undenkbar, weil dann die dauernden Abweichungen – écarts
Ich weiß wohl, daß die Annahme einer Gleichheit auf 2 097 152 Sätze willkürlich ist. Aber das fällt weg, wenn ich anstatt einer bestimmten Zahl die Anzahl einfach auf n setze. Dann wird jeder zugeben, daß n/2 mal Rot und n/2 mal Schwarz kommen muß, oder wenigstens, daß man auf kein anderes Verhältnis eine Berechnung gründen kann, und hierum ist es uns in diesem Falle zu tun.
Zum Überfluß führe ich noch an, daß ich bei der Behandlung der simple chance der Einfachheit halber nur von Rot und Schwarz sprach. Alles, was ich darüber sagte, paßt ebenso auf alle anderen Chancen, die bei jedem Satze den Wert ½ haben, und deren Art man willkürlich ausdehnen kann. Es gibt z.B. ebensoviel coups, die der Farbe folgen, wie solche, die es nicht tun. Ebenso viele, die dem vorletzten gleich sind, und die ihm nicht gleich sind. Ebenso viele, die eine beginnende Serie zur Intermittenz abbrechen, wie solche, die sie zu einem Zweischlag machen u.s.w.
Zu all diesen Verhältnissen sind auch die zu fügen, welche auf die relative Häufigkeit gerader und ungerader Serien gegründet sind. Die Zahl der geraden Serien beträgt die Hälfte der ungeraden, aber die auf dies Verhältnis gegründeten coups sind, ebenso wie die Chancen auf Rouge oder Noir unterworfen dem Gesetz der durch scheinbar willkürliche Abweichungen vielfach unterbrochenen, aber gerade dadurch schließlich zustande kommenden Gleichheit.
Dieselbe Betrachtung paßt auf die Zahl Sätze, die der Spieler gewinnt oder verliert, gleichgültig, ob er durchgehends dieselbe Farbe wählt, ob er fortwährend oder ab und zu, nach Laune, wechselt, ob er auf oder gegen die »Gagnante« spielt, ob er sein Glück in Intermittenzen oder Serien sucht, ob er auf das Verhältnis ungerader oder gerader Serien spekuliert ... immer bleibt der Wert jedes Einsatzes
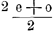
Nicht mehr, nicht weniger.
Diese allzu einfache Wahrheit ...
Es ist nicht so ganz überflüssig, sie dem Spieler vorzuführen! Er scheint doch dadurch, daß er das Geldstück, das in seiner Börse 1 beträgt, auf den Spieltisch legt, die Meinung
zu äußern, daß
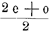 mehr beträgt als 1. Mit anderen Worten: die gleiche Chance, seine Einheit zu 2 erhöht oder zu 0 verringert zu sehen, scheint ihm der Sicherheit, daß er 1 besitzt, vorzuziehen – oder er hält die Chance nicht für gleich.
mehr beträgt als 1. Mit anderen Worten: die gleiche Chance, seine Einheit zu 2 erhöht oder zu 0 verringert zu sehen, scheint ihm der Sicherheit, daß er 1 besitzt, vorzuziehen – oder er hält die Chance nicht für gleich.
Diese einfache Betrachtung sollte in gewissem Sinne ausreichen, um alle Spieler von ihren Systemen zu kurieren.
In der Spielerwelt aber ist ein Adagio im Umlauf, das die Genesung als unmöglich kennzeichnet. Man sagt: »Qui a joué, jouera – wer gespielt hat, spielt wieder!«
Ich meine, es gibt wohl ein Mittel, um jemand vom Spiel zu kurieren. Man muß den Patienten rechnen lehren. Rechnen, mit Zahlen arbeiten, das gehört zu der Naturkunde, die ich als bewährtes Mittel gegen allerlei Aberglauben empfehle. Die Anbetung des Rouge et Noir hält ebensowenig wie andere Theologien gegen den Einfluß des Logos, der Vernunft, stand. Wer töricht genug ist, einen Gott um Regen oder Trockenheit oder Genesung von einer Krankheit zu bitten, der wird bei derselben Arzenei Hilfe finden, die ihn von der Furcht kuriert, die Gagnante zu beleidigen, oder von dem festen Vertrauen auf eine »Figur.«

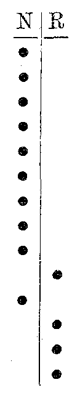
Von »Figuren« habe ich noch nicht gesprochen. Es gibt Leute am grünen Tische, die ihr Heil in einer mehr oder minder willkürlich aufgestellten Kombination von Sätzen suchen. Sie spielen weniger auf Intermittenzen noch auf Serien, sondern auf eine vorausbestimmte besondere Reihenfolge der Farben einer gewissen Gruppe. Man nimmt an, hofft oder glaubt, z.B. daß herauskommen werden: dreimal Rot, einmal Schwarz, zweimal Rot, fünfmal Schwarz, einmal Rot, einmal Schwarz, und dann noch einmal Rot. Auf den durch die Bank gelieferten Spielkärtchen, auf denen man die Sätze mit einem Stecknadelstich bezeichnet, sähe diese Figur so aus (Siehe nebenstehende Figur):
Die meisten wagen natürlich ihre Phantasie nicht daran, eine sehr große Zahl von Sätzen vorauszusagen. Was sie veranlaßt, die gewählte Figur für wahrscheinlicher zu halten als eine andere, ist mir unbekannt. Wenn wir den Gründen nachforschten, die sie dazu veranlassen, kämen wir vielleicht wieder in die angenehme Nachbarschaft der bewußten Kreuzspinne.
Vielleicht hat man auch ausgerechnet, daß man diese Figur jetzt mit großer Wahrscheinlichkeit erwarten könne, weil sie sich lange nicht gezeigt hat.
Dies lange Ausbleiben ist nicht so auffallend, wenn man bedenkt, daß die Reihenfolge von vierzehn Sätzen sich auf 16 384 verschiedene Arten zeigen kann.
Wer daher sein Glück von dieser einen Art abhängig macht, nimmt ein Los in einer Lotterie von 16 384 Nummern, in denen nur ein Gewinner ist.
Ich brauche wohl nicht zu sagen, daß nicht der geringste Grund vorhanden ist, einer nach Laune bestimmten Abwechselung vor einer regelmäßigen Serie den Vorzug zu geben. Vierzehn Schwarze, vierzehn Rote haben genau so viel Existenzberechtigung wie die Folge, die ich eben ganz willkürlich zu einer sogenannten Figur zusammensetzte.
Ich tat das auch durchaus nicht, um mich in die Gewinnhoffnungen zu vertiefen, die sich auf solche Spielerei gründen. Mein Ziel ist, nach diesen Figuren auf ein ganz anderes Terrain überzugehen, auf das Regelmaß von allem, was ist.
Jeder Spieler weiß, daß jeder Satz ungewiß ist. Und doch gibt er dieser oder jener Farbe den Vorzug. Was veranlaßt ihn dazu?
Er muß doch der Ansicht sein, daß die Natur eine gewisse Ordnung beobachtet.
Gleichzeitig aber scheint er es sonderbar zu finden, wenn diese Ordnung sich deutlich offenbart.
Darin liegt ein sonderbarer Widerspruch.
Nehmen wir an, daß auf dem Spielkärtchen, in dem die ganze Taille eingestochen ist, sich eine der Figuren zeigt, die hier (S. 175) in den fünf Beispielen gezeigt worden.
Mit welchem Rechte finden wir die scheinbar unregelmäßige Abwechselung im ersten Beispiel weniger auffallend als die Regelmäßigkeit in den anderen Beispielen?
Mancher wird es sogar geradezu für unmöglich halten, daß eine ganze Taille nur aus Intermittenzen besteht wie im zweiten Beispiel.

Oder daß eine so regelmäßige Viererfolge möglich wäre, wie bei Nummer 3. Daß die ganze Taille in zwei gleiche Hälften zerfiele wie in Nummer 4. Und nun gar – aber auch das ohne mehr Grund – daß sie ganz und gar aus schwarzen Coups bestehen sollte, wie in Nummer 5.
Bei einigem Nachdenken wird man jedoch zugeben müssen, daß alle diese Taillen nicht allein möglich sind, sondern daß jede einzelne davon genau so viel Anspruch auf Existenzberechtigung hat wie irgend eine andere Gruppe von 27 Sätzen.
Immer aber bleiben viele, die die Regelmäßigkeit ... unnatürlich finden und dahinter etwas anderes suchen als den Lauf des sogenannten »Schicksals.« Der Zufall – mit oder ohne indiskrete Bemühung einer Gottheit – kann wohl Taillen nach Modell 1 machen, aber die anderen gehen über seine Kraft. Das Schicksal ist hier schwacher als der Mensch sogar, als ein Kind – denn wir konnten aus dem Quinetschen Fasse so viel schwarze Kügelchen herausholen als wir wollen!
Um diesen Widerspruch in der Auffassung recht deutlich zu machen, nehme ich einmal einen Spieler an, der ein Krüppel, lahm oder krank ist. Er sitzt vielleicht gefangen, aber er hat – mit Hilfe der heiligen Morfondaria natürlich – von Rot geträumt.
Er schätzt sich glücklich, daß er einen »alten treuen« Diener hat, den er ins Kurhaus schickt, um ein Goldstück auf die geträumte Farbe zu setzen.
Der alte Getreue kommt wieder mit der Meldung, daß der Einsatz futsch ist, »weil Schwarz herauskam.«
Wenn nun unser Gefangener behauptete, das wäre unmöglich, und den Diener wegen Unehrlichkeit wegjagte, handelte er wie ein Narr. Die Möglichkeit – wir sind hier mitten in der Wahrscheinlichkeitslehre – daß der alte Getreue mit einem Male ein Spitzbube geworden sein sollte, kommt ihm kleiner vor, als daß diesmal gegen seine Erwartung Schwarz gekommen sein sollte.
Er glaubt also, was der Mann berichtete, und gibt ihm nun zwei Stücke, wieder um sie auf Rot zu setzen.
Der Knecht kommt wieder mit der Botschaft, daß der Ausgang Schwarz war.
Hat er jetzt die zwei Stücke gestohlen? Oder vielleicht gar vier? Zwei, wenn er sich die Stücke zueignete, ohne zu setzen, vier, wenn er gesetzt und gewonnen hat?
Unser Gefangener denkt nicht klein. Er zweifelt wieder nicht an der Rechtschaffenheit seines Dieners und schickt ihn wieder, um auf Rot zu setzen, diesmal mit vier Stücken.
Heraus kam Schwarz!
Der Knecht wird jetzt mit
acht Stücken geschickt ...
Heraus kam Schwarz.
Mit
sechzehn Stücken ...
Schwarz.
Mit
zweiunddreißig Stücken ...
Schwarz.
Mit vierundsechzig Stücken ...
Schwarz!
Ich kann hier abbrechen.
Der Leser denke sich nun einmal das Maximum weg, das soll es nicht geben, und er setze das Hin- und Herlaufen des Dieners fort, bis der Herr ihn als Dieb davonjagt, Frage: beim wievielsten Satz gibst du dem Herrn recht? Beim wievielsten Satz hättest du, Leser, den alten Getreuen selber davongejagt?
Es kann doch nicht immer Schwarz kommen, nicht?
Immer? Nein.
Aber ich habe selber zweiundzwanzig Sätze von derselben Farbe hintereinander gesehen, ohne noch zu wissen, ob die Serie damit endete. Die Taille war aus, und ich wartete nicht ab, ob die folgende vielleicht die Serie fortsetzte.
Warum nicht! Alte Spielratten sprechen von höheren Serien, und die Wahrscheinlichkeit ist, daß ich, der den Spielsaal selten besucht, nicht gerade der seltenen allerhöchsten beigewohnt habe. Es soll welche von vierunddreißig gegeben haben. Wer sich darüber wundert, vergißt wieder, daß jede andere Gruppe von vierunddreißig Sätzen ebenso selten kommt. Der Nenner des Bruches dieser Wahrscheinlichkeit ist 17 179 868 184 = 2 x 2 x 2 x 2 ... (34mal).
Jeder erste Satz ist unfehlbar eine Abweichung von der Gleichheit. Die herausgekommene Farbe steht zu der nichtherausgekommenen wie 1 zu 0. Nach dem zweiten Satz ist die Möglichkeit der Erhöhung der Abweichung ebenso groß wie die des Gleichwerdens. Die Farben stehen dann wie 2 zu 0 oder wie 1 zu 1. Auf vier Möglichkeiten
| s
s |
oder | s
r |
oder | r
r |
oder | r
s |
ist die Summe der Abweichungen 4, d.h. im Mittel 1. Dies, geteilt durch die Zahl der Sätze – in diesem Falle 2 – kann die mittlere Abweichung auf zwei coups auf ein halb für jeden Satz festsetzen.
Drei Sätze können sich auf acht Weisen zeigen:
| s | s | s | s | r | r | r | r |
| s | s | r | r | s | s | r | r |
| s | r | s | r | s | r | s | r |
Die Summe der Abweichungen ist 12, oder, geteilt durch die Zahl der Variationen, 1 1/2 was sich zur Zahl der Sätze verhält wie 1:2. Vier Sätze zeigen sich als:
| s | s | s | s | s | s | s | s | r | r | r | r | r | r | r | r |
| s | s | s | s | r | r | r | r | s | s | s | s | r | r | r | r |
| s | s | r | r | s | s | r | r | s | s | r | r | s | s | r | r |
| s | r | s | r | s | r | s | r | s | r | s | r | s | r | s | r |
Die Summe der Abweichungen ist 24. Dies beträgt auf 16 Möglichkeiten 1½; die vermutliche Abweichung auf 4 Sätze beträgt also ⅔ auf den Satz.
Diese Berechnung hat nicht den geringsten Wert, wenn man sie auf kleine Gruppen anwendet. Ja sie scheint sogar ungereimt, da alle Abweichungen aus ganzen Sätzen entstehen und also jeder Bruch undenkbar ist. Das ist aber der gewöhnliche Fehler einer Mitte. Ich glaube nicht, daß man auf andere Weise zu einem Urteil über die vermutlichen Abweichungen für eine größere Zahl von Sätzen kommen kann. Als Beispiel für den, der sich damit befassen will, gebe ich die folgende Aufstellung:
| Zahl der Sätze | Möglichkeiten der Zusammenstellung d. Gruppe | Summe der Abweichungen | Mittlere Abweichung auf eine Gruppe | Mittlere Abweichung auf den Satz |
| 1 | 2 | 2 | 1 | 1 |
| 2 | 4 | 4 | 1 | 1/2 |
| 3 | 8 | 12 | 1 1/2 | 1/2 |
| 4 | 16 | 24 | 1 1/2 | 3/8 |
| 5 | 32 | 60 | 1 7/8 | 3/8 |
| 6 | 64 | 120 | 1 7/8 | 5/16 |
| 7 | 128 | 280 | 2 3/16 | 5/16 |
| 8 | 256 | 560 | 2 3/16 | 35/128 |
| 9 | 512 | 1260 | 2 59/128 | 35/128 |
| 10 | 1024 | 2520 | 2 59/128 | 68/256 |
Es ist mir nicht deutlich, wie man diese Berechnung mit jenem Wurzelverhältnis, das ich einmal anführte, in Zusammenhang bringen kann. Auch sehe ich nicht, wie sie dem Spieler nützen kann. Zum ersten weiß er nicht, nach welcher Seite die Abweichung stattfinden wird, und da jede der beiden Farben den gleichen Anspruch hat, voraus zu sein, folgt hieraus das zweite: daß bei jedem Übergang ein Punkt vollkommener Gleichheit muß erreicht und passiert werden. Der Lauf der Sätze ist ein fortwährender Kampf zwischen Abweichungen und Gleichwerden und kann mit dem Auf- und Abgehen zweier Wagebalken verglichen werden.
Daß dieses Oscillieren uns weniger regelmäßig scheint, liegt daran, daß wir gewöhnlich die unendlich vielen Arten von Gleichgewicht unbeachtet lassen, die durch die Natur der Dinge erreicht werden müssen.
Es ist vielleicht eine Reihenfolge vorhanden, wie diese:
Da würden wir erwarten, daß jetzt Rot folgte, weil die Schwarzen (Noir) sechs coups voraus sind. Gleichzeitig sehen wir aber in diesem Schema zehn Sätze, die »der Farbe folgen« und nur drei, die mit der vorigen nicht übereinkommen. Um der Gleichheit in dieser Hinsicht willen müßte der fünfzehnte Satz nach Rot also Schwarz sein. In diesem Falle schlösse aber der rote Dreischlag als ungerade Serie, was nun schon das dritte Mal wäre, ohne eine einzige gerade Serie. Hieraus müßte man wieder schließen, daß der fünfzehnte Satz Rot sein würde, damit aus diesem Dreischlag ein Vierer würde. Da kommen wir aber wieder in Konflikt mit den Ansprüchen der kleinen Serien und Intermittenzen, die in diesem Schema nicht genug vertreten sind. Die wollen ihre Rückständigkeit auch einholen. Es ist also als fünfzehnter Satz ein schwarzer zu erwarten oder ... ein roter!
So ist es. Denn wir verlieren uns in Unsicherheit.
Und ich sprach noch nicht einmal von dem Oscillieren der Abweichungen, von dem Abweichen der Abweichungen, die ganz selbständig bald Intermittenzen, bald wieder eigensinnig eine Zeitlang dieselbe Seite wählen. Auch darin kommt schließlich Gleichheit zustande, aber nur auf Kosten scheinbarer Unregelmäßigkeiten, auf die der scharfsinnigste Rechner kein System gründen kann.
Ach, ich beginne zu fürchten, daß meine Studien nicht geeignet sein werden »pour gagner la banque« – die Bank zu sprengen. Zum Glück sorgen andere Spielprofessoren dafür. Selbst Schlüngelhans soll im Zuchthaus seine Zeit einem unfehlbaren System gewidmet haben ...
In der Voraussetzung, daß er nicht rechnen kann, billige ich ihm mehr Hoffnung auf Erfolg zu als mir selber, und ich gebe dem Leser die Erlaubnis, den Früchten seiner Muße erwartungsvoll entgegenzusehen. Meine Untersuchungen führen nicht weiter als zu der Sicherheit, daß der Ausschlag jedes coups ebenso unsicher ist Wie der aller anderen, und daß man daher nur im besonderen Falle Grund hatte
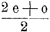 als größer als e anzusehen.
als größer als e anzusehen.
Dieser Fall muß gedacht werden können.
Jemand besitzt e und muß eine Reise machen, zu der er mehr als e, aber nicht mehr als 2 e (sagen wir r) nötig hat. Um das ihm Fehlende zu erhalten, müßte er darum schreiben, aber das Warten auf Antwort verursacht ihm u Unkosten. Wenn er nun sein e auf simple chance setzt, hat dies Geld für ihn als Einsatz mehr Wert als wenn er es im Geldbeutel behielte.
Beim Verlust nämlich hat er einen negativen Besitz von u + r. Er hat nichts in der Kasse und muß Unkosten und Reise bezahlen.
Im Fall des Gewinns hat er 2 e–r. Er vermeidet die Unkosten für das Warten und kann die Reise bestreiten.
Wenn er nicht spielt, hat er e in der Kasse, ist aber Unkosten und Reise schuldig. Sein Besitz ist dann: e–r–u.
Da nun der mittlere Wert der beiden Möglichkeiten, wenn er spielt, beträgt
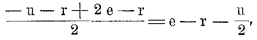
so ergibt sich, daß e als Einsatz auf simple chance 1/2 u (d.h. die Hälfte der zu machenden Unkosten) mehr wert ist als e in seiner Börse.
Es versteht sich, daß diese Erwägung unrichtig wird, wenn man u/2 kleiner setzt als e/74 oder e/79, weil in diesem Falle die Aussicht, die Unkosten zu gewinnen, nicht gegen zéro oder refait standhält.
Man wird weiter eingeladen, das durch mich gewählte Beispiel der Dringlichkeit auf Dinge größeren Interesses auszubreiten. Ich redete nur von Reisekosten und von einem Satz auf simple chance. Es liegt auf der Hand, daß ein Kaufmann ein großes Interesse haben kann, in einem bestimmten Augenblick über eine gewisse Summe zu verfügen, deren Verlust weniger Schaden bringt als von dem möglichen Gewinn Vorteil erwartet werden kann. Es wird behauptet, daß das an der Frankfurter Börse wohl bekannt ist, und daß das Spekulieren in Staatspapieren ziemlich regelmäßig abwechselt mit der Übung der Theorie von simple chance. Warum dies stets »unter der Rose« geschieht, verstehe ich nicht. Die Effektenmenschen werden sich doch nicht einbilden, daß sie herunterstiegen, wenn sie ihr Comptoir an den grünen Tisch verpflanzen?
Ja, das glauben sie!
Es ist albern, eingebildet, unaufrichtig, heuchlerisch oder vielleicht statt alledem: dumm, aber es ist so!
Und nicht bloß Effektenmenschen.
Auch andere Spekulanten ...
Davon etwas im folgenden Kapitel.