Gesetz, Kausalität und Wahrscheinlichkeit

Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++

Über den Begriff der Ganzheit.

(Zuerst erschienen in »Wissenschaftlicher Jahresbericht der Philosophischen Gesellschaft an der Universität zu Wien für das Vereinsjahr 1933/34 und 1934/35«.)

Die Philosophie ist keineswegs nur, wie ein großer Spötter meinte, der »Mißbrauch einer eigens zu diesem Zwecke erfundenen Terminologie«, sondern man kann ebensogut der Auffassung sein, daß sie überhaupt keiner besonderen Kunstausdrücke bedarf. Sie vermag, wie das Beispiel der größten Denker lehrt, tiefste Wahrheiten mit den alltäglichen Worten der Umgangssprache auszudrücken – aber auch, wie andere Beispiele zeigen, dieselben alltäglichen Wörter zu den kühnsten Spekulationen und zu unsinnigem Gerede mißbrauchen. Was ist mit dem unschuldigen Verbum »Sein« seit der Zeit der Eleaten nicht alles angestellt worden! So haben die harmlosesten Wörter des täglichen Gebrauchs ein bewegtes philosophisches Schicksal.

Wenn in der Umgangssprache von einem »Ganzen« im Gegensatz zu seinen »Teilen« geredet wird, so ist damit gewöhnlich keinerlei Unklarheit verbunden; wenn aber, wie das etwa schon bei Aristoteles geschah, diese Termini benutzt werden, um einen Grundgedanken eines philosophischen Systems zu formulieren, so entsteht eine schwere Problematik. Sie bleibt so lange unaufgelöst, als man sich nicht bis ins einzelne und letzte Rechenschaft darüber gibt, in welcher Weise man eigentlich die Worte gebrauchen will. Denn mit dem Übergang vom Alltäglichen zum Theoretischen und Allgemeinen hat man eine neue Verwendung der Termini eingeführt, mit der sich erst dann ohne Unklarheit und Widersprüche arbeiten läßt, wenn man sich über ihre Bedeutung, das heißt über die Regeln ihres Gebrauchs, restlos geeinigt hat.

Aus dem σύνολον des Aristoteles ist die »Ganzheit« oder »Totalität« der modernen philosophischen Schriftsteller geworden. Sie führen diese Worte (oder andere von ähnlicher Bedeutung) ohne Unterlaß im Munde und glauben damit auf dem Wege zur Lösung der größten Probleme zu sein. »Ganzheit« ist fast zu einem Zauberwort geworden, von dem man Befreiung aus allen Schwierigkeiten erhofft.

Drei fundamentale Fragen besonders glaubt man mit Hilfe dieses Begriffes beantworten zu können: die Frage des Verhältnisses des Organischen zum Anorganischen (das Lebensproblem), die Frage nach dem Verhältnis des Physischen zum Psychischen (das Leib-Seele-Problem) und die Frage nach dem Verhältnis des Individuums zur Gesamtheit (das Gemeinschaftsproblem). Es läßt sich auch so formulieren: Man vermeint das Zauberglas gefunden zu haben, welches die wesentlichen Beziehungen zwischen Psychologie, Biologie, Physik und Soziologie endgültig mit vollkommener Klarheit sichtbar macht. Und zwar wird von den meisten Schriftstellern der Begriff der Ganzheit zur Aufstellung der Behauptung benutzt, daß das Organische vor dem Anorganischen, das Psychische vor dem Physischen, die Gesellschaft vor dem Individuum durch ganz besondere Eigenschaften ausgezeichnet sei, welche eine Zurückführung des einen auf das andere prinzipiell ausschlössen. Nur einige wenige Psychologen suchen mit Hilfe des Ganzheitsbegriffs – unter dem Namen der »Gestalt« – die entgegengesetzte Meinung zu stützen: daß nämlich die Grenzen zwischen jenen Gebietspaaren keineswegs unüberschreitbar seien, und daß kein prinzipieller Gegensatz der Begriffsbildung zwischen ihnen bestünde.

Die folgenden Betrachtungen verfolgen den Zweck, Behauptungen dieser Art kritisch zu prüfen; und zwar benütze ich dazu die Methode, die ich für die philosophische Methode schlechthin halte: ich forsche nämlich nach dem Sinn solcher Behauptungen. Es gilt nur genau festzustellen, was denn mit den verschiedenen Sätzen, in denen das Wort »Ganzheit« auftritt, eigentlich gesagt sein soll; es handelt sich einfach um die Festlegung der logischen Grammatik dieses Wortes (und des Wortes »Teil«). Da stellt sich denn heraus, daß die Autoren derartiger Sätze wohl oft etwas ganz Bestimmtes und Richtiges mit ihnen gemeint haben, daß es ihnen aber fast immer nur undeutlich vorschwebte und infolgedessen falsch ausgedrückt wurde. Daher stimmen ihre Folgerungen im allgemeinen nicht, und die darauf erbauten Philosopheme müssen zusammenbrechen.

Der besondere Gebrauch, der in der philosophischen Literatur der Gegenwart von dem Ganzheitsbegriff gemacht wird, besteht bekanntlich darin, daß man zwei verschiedene Arten von Gebilden unterscheidet. Erstens solche, die, wie man sagt, eine bloße »Summe« der Teile darstellen, aus denen sie »zusammengesetzt« sind, wie etwa ein Haus aus einzelnen Steinen, eine Torte aus Schichten von Kuchen und Creme. Meist wird behauptet, daß in der anorganischen Natur keine anderen Gebilde als nur diese vorkommen; stets aber läßt man sie als völlig unproblematisch beiseite, um die ganze Aufmerksamkeit der zweiten Art von »Ganzen« zuzuwenden, nämlich denjenigen, die, wie man sagt, mehr sind als eine bloße Summe ihrer Teile und ganz andere Eigenschaften haben als diese; wie etwa eine Melodie etwas ganz anderes ist als die einzelnen Töne, aus denen sie besteht; ein Organismus viel mehr als ein bloßer »Haufen« von Zellen. Solche Gebilde meint man allein, wenn man von einem »Ganzen« in prägnantem Sinne spricht; und gewöhnlich wird die Meinung vertreten, daß sie nur im Reiche des Organischen, des Psychischen, des Geistes, der Gesellschaft zu finden seien, und daß eben hierin der charakteristische Unterschied zwischen den Gebieten des Lebens und des Geistes auf der einen Seite und der toten Natur auf der anderen Seite bestehe.

Das Wort »Gestalt«, welches in dieser besonderen Bedeutung zunächst bei Gebilden verwendet wurde, die den Gegenstand der Psychologie bilden, dann aber von W. Koehler auch auf physische Ganzheiten übertragen worden ist, dürfen wir für unsere Zwecke als völlig gleichbedeutend mit dem Worte »Ganzheit« betrachten.

Man pflegt zwei Kriterien dafür anzugeben, daß ein Komplex ein echtes Ganzes oder eine Gestalt ist und nicht eine »bloße Summe«: 1. Die Eigenschaften des Gebildes (manchmal fügt man hinzu: seine Wirkungen) sind nicht aus den Eigenschaften (bzw. Wirkungen) seiner Teile zusammensetzbar (manchmal sagt man: ableitbar). 2. Es ist »transponierbar«, das heißt, es kann in seinen charakteristischen Zügen unverändert bleiben, auch wenn keiner seiner Teile erhalten bleibt. Eine Melodie zum Beispiel hat Eigenschaften und Wirkungen von anderer Art als die einzelnen Töne, aus denen sie gebildet ist; die Verhaltungsweisen eines lebendigen Organismus sind ganz andere als die der Zellen oder gar der Moleküle, die ihn zusammensetzen. Beide sind ferner transponierbar, denn eine Melodie bleibt wesentlich dieselbe, wenn ich jeden ihrer Töne durch einen um eine Terz höheren Ton ersetze; ein Organismus behält alle seine charakteristischen Eigenschaften, obgleich alle seine Teile durch den Stoffwechsel fortwährend durch andere ersetzt werden, ja vielleicht etwa durch den Prozeß des Alterns sich beträchtlich ändern.

Jemand, dem der Ganzheitsbegriff an diesen Beispielen erläutert wurde, wird den Sinn der beiden Kriterien erfaßt zu haben glauben; ist er nun auch wirklich imstande, sie allgemein anzuwenden? Dies kann nur dann der Fall sein, wenn die Kriterien selbst ganz eindeutige Anweisungen dazu enthalten. Aber wie steht es damit? Was bedeuten die Ausdrücke »charakteristische Züge«, »zusammensetzbar«, »ableitbar«? Es wäre ein schlimmer Fehler, anzunehmen, daß solche Worte, wie »Summe«, »additive Zusammensetzung« und ähnliche, die gewöhnlich ohne Erläuterung gebraucht werden, bereits eine klare und allgemein bekannte Bedeutung besäßen.

Nehmt nur das Wort »zusammensetzen«! Wir sagen von einem Gebäude, es sei aus Steinen zusammengesetzt und wollen damit auf ein räumliches Nebeneinander der Steine hindeuten; wir sagen von einer Melodie, sie sei aus Tönen zusammengesetzt und meinen damit ein bestimmtes zeitliches Nacheinander der Töne; wir sagen aber auch von einem Akkord, daß er aus Einzeltönen zusammengesetzt sei, und in diesem Falle soll es heißen, daß die Töne zeitlich zugleich erklingen: es liegt also jedesmal ein anderer, teilweise geradezu entgegengesetzter Gebrauch desselben Wortes vor, und beliebig viele andere Verwendungsweisen sind denkbar. Wenn uns ein Physiker das Parallelogramm der Kräfte erklärt, so spricht er von einer Zusammensetzung von Vektoren zu einer Resultanten, und die Philosophen streiten darüber, ob es sich hier um einen »additiven«, »summativen« Prozeß handle oder nicht, ohne zu bedenken, daß dies schlechterdings nichts anderes ist als eine rein terminologische Frage, denn es steht uns frei, beliebig festzusetzen, wann wir von einer Summe sprechen wollen und wann nicht.

Man vergißt zu leicht, daß die Bedeutung des Wortes »Summe« zunächst nur für einen einzigen Fall eindeutig festgelegt ist, nämlich für Zahlen. Will man es in anderen Fällen verwenden, so bedarf es jedesmal einer besonderen neuen Definition, und die ist allein durch praktische Rücksichten bestimmt, sie richtet sich nach den vorliegenden Bedürfnissen. Die Physik hat zum Beispiel nicht einen Begriff »Summe zweier Temperaturen« definiert, wohl aber den einer Summe zweier Geschwindigkeiten.

Es lohnt der Mühe, an Beispielen wie den eben erwähnten die Willkür des Summenbegriffs (und damit seines Gegenteils, des Ganzheitsbegriffs) klarzumachen. Werfen wir also zunächst einen Blick auf die physikalische Temperatur!

Vielleicht sagt jemand, es komme doch vor, daß in einer physikalischen Formel der Ausdruck T₁ + T₂ auftrete, worin sowohl T₁ wie T₂ Temperaturen bedeuten – habe man hier also nicht eine »Summe zweier Temperaturen« vor sich? Wir antworten: wenn du willst, kannst du es so nennen; aber der Ausdruck T₁ + T₂, der ja in der physikalischen Formel für eine bestimmte Zahl steht, hat darin jedenfalls nicht die Bedeutung einer Temperatur, wie sie physikalisch (durch ein bestimmtes Meßverfahren) definiert ist. Denn ob nun zum Beispiel die beiden T die Temperaturen zweier verschiedener Körper oder eines und desselben Körpers zu verschiedenen Zeiten bedeuten: jedenfalls behauptet die Formel im allgemeinen nicht, daß nun irgendwo an einem Körper die Temperatur von der Größe T₁ + T₂ gemessen werden könnte oder müßte. Umgekehrt: ich kann sehr wohl sagen, daß ein Körper die Temperatur (15 + 5)° Celsius habe; damit habe ich ihm aber einfach die Temperatur 20° zugeschrieben, der Unterschied liegt allein in der Schreibweise (die arithmetischen Regeln wie die Formeln 15 + 5 = 20 sind ja nur Regeln für die Umformung symbolischer Ausdrücke). Ich habe nicht etwa die Temperatur des Körpers aus zwei Temperaturen, einer von 15° und einer von 5°, zusammengesetzt.

Wie steht es nun mit dem Ausdruck v₁ + v₁, wo jeder der beiden Summanden die Maßzahl einer Geschwindigkeit bedeutet? Er bezeichnet eine bestimmte Zahl auch dann, wenn v₁ und v₂ die Geschwindigkeit zweier verschiedener Körper in bezug auf zwei beliebige verschiedene Systeme bedeuten; aber definitionsgemäß sprechen die Physiker von einer »Zusammensetzung« oder »Addition« zweier Geschwindigkeiten nur in einem ganz bestimmten Fall, nämlich in folgendem: Es sind drei Körper A, B, C vorhanden und A hat in bezug auf B die Geschwindigkeit v₁, B in bezug auf C die Geschwindigkeit v₂; dann nennt man die Geschwindigkeit v, welche A in bezug auf C besitzt, die Resultante (Vektorsumme) von v₁ und v₂. Dabei ist – diese Bemerkung ist von höchster Wichtigkeit – jede der drei Geschwindigkeiten als eine Zahl definiert, die sich als Resultat eines ganz bestimmten Meßverfahrens ergibt. Welchen Wert dieses Meßverfahren für v, also für die Geschwindigkeit von A relativ zu C liefert, wenn man für die Geschwindigkeit von A relativ zu B den Wert v₁ und für die von B relativ zu C den Wert v₂ gefunden hat, kann selbstverständlich nur die Erfahrung lehren. 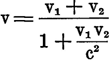Für den Fall, daß v₁ und v₂ gleichgerichtet sind, zeigt sich bekanntlich, daß Formel

(Einsteinsches Additionstheorem), worin c die Lichtgeschwindigkeit bedeutet und in der Formel deswegen vorkommt, weil sie eine Rolle spielt in dem Meßverfahren, durch welches die Geschwindigkeiten definiert sind.

Nach diesen Erläuterungen erscheint es fast unbegreiflich, daß manche Kritiker immer wieder behaupteten, es müsse notwendig v = v₁ + v₂ sein, da man sonst durch Verstoß gegen die Arithmetik eine logische Absurdität begehe. Der Fehler liegt (und deswegen sprechen wir hier davon) in einer völligen Unklarheit über den Begriff der Summe. Man sieht nicht, daß die Summe zweier Zahlen und die »Summe« zweier physikalischer Größen ganz verschiedene Dinge sind, daß mit der Definition des einen die Definition des anderen noch nicht gegeben ist, sondern besonders aufgestellt werden muß. Die Maßzahl der physikalischen »Summe« zweier Größen ist etwas ganz anderes als die arithmetische Summe der Maßzahlen der beiden Größen.

Die Verwechslung zeigt sich recht deutlich in der Formulierung, welche H. Driesch seiner Bestreitung des Additionstheorem gibt. Er sagt (Relativitätstheorie und Weltanschauung, 2. Aufl., Seite 39): »c + v₁ bleibt allemal = c + v₁ und ›ist‹ nie = c«. Er will nämlich behaupten, daß die resultierende Geschwindigkeit bei der Zusammensetzung der Geschwindigkeiten c und v₁ stets c + v₁ sein müsse und nie c sein könne, und dies spricht er in dem zitierten Satze aus, weil er voraussetzt, daß c + v₁ den Wert der Resultierenden bezeichnen müsse, weil sie ja als »Summe« von c und v₁ definiert ist. Die Relativitätstheorie lehrt aber nicht den Unsinn, den Driesch ihr zuschreibt, nämlich, daß c + v₁ = c, sondern vielmehr, daß die resultierende Geschwindigkeit = c wird, falls eine der Komponenten = c ist. Die oben mitgeteilte Formel des Additionstheorems liefert nämlich v = c, wenn man in ihr v₂ = c setzt.

Fußnote aus technischen Gründen als Anmerkung wiedergegeben. Re für Gutenberg.
Daß es auch heute noch Leute gibt, welche der Relativitätstheorie diesen Unsinn in die Schuhe schieben wollen, kann angesichts der Mentalität der Gegner jener Theorie nicht wundernehmen; für unmöglich aber hätte man es wohl gehalten, daß jemand behaupten könnte – und zwar auf Grund der obigen Textstelle – ich selbst hätte jenen Unsinn verteidigt. Es ist jedoch wirklich behauptet worden, und zwar von Herrn O. Kraus, ord. Professor der Philosophie an der deutschen Universität in Prag. In dem Bändchen »Zur Philosophie der Gegenwart. Vorträge und Reden anläßlich des 8. Internationalen Philosophenkongresses in Prag, gehalten von Mitgliedern der Brentano-Gesellschaft. Prag 1934« ist ein »Rundfunk-Epilog zum Philosophenkongreß« abgedruckt, der von dem Genannten gezeichnet ist und vermutlich auch vor dem Mikrophon gesprochen wurde. Es heißt dort auf Seite 67: »Es ist bezeichnend, daß von der Relativitätstheorie während des ganzen Kongresses nur einmal die Rede war, als Schlick aus Wien neuerlich die Absurdität rechtfertigen wollte, daß c - v = c sei.«

Herr O. Kraus kann sich nicht damit entschuldigen, daß ihm meine Worte nicht bekannt gewesen wären, denn der ganze Text meines Vortrages lag in dem hier wiedergegebenen Wortlaut zu Beginn des Kongresses vor und wurde den Teilnehmern eingehändigt. Herr Kraus kann sich nur auf diesen gedruckten Wortlaut gestützt haben, denn beim mündlichen Vortrag in Prag habe ich, um Zeit für andere Ausführungen zu gewinnen, die ganze obige Stelle überhaupt nicht gebracht.

Wenn auch das Minus-Zeichen bei Kraus statt des bei mir stehenden Plus-Zeichens vielleicht auf eine gewisse Flüchtigkeit der Lektüre deuten könnte, so ist mein Text doch so eindeutig und klar, daß der Leser es unmöglich finden wird, die zitierte Behauptung des Herrn Kraus durch ein Versehen zu erklären (übrigens würde auch eine Fahrlässigkeit, durch die dem Gegner genau das Gegenteil seiner wirklich geäußerten Meinung zugeschrieben wird, unter den vorliegenden Umständen eine gröbliche Verletzung der literarischen Pflicht darstellen). Man muß also vermuten, daß Herr Kraus seine Behauptung nur aufstellte, weil er eine ihm unsympathische philosophische Richtung diskreditieren wollte.

Da Summen (additive Komplexe) und Ganzheiten (nicht additive Komplexe) korrelative Begriffe sind, so kann man den einen nicht verstehen, ohne sich über den anderen klar zu sein. Da wir nun bei dem führenden Ganzheitstheoretiker der Gegenwart einen schweren Irrtum hinsichtlich des Summenbegriffs gefunden haben, so werden wir seine Versuche, den Ganzheitsbegriff von ihm abzugrenzen, mit doppelter Wachsamkeit betrachten müssen.

So stoßen wir auf allerlei Schwierigkeiten in unserem Bemühen, eine klare und eindeutige Verwendung für das Wort »Ganzheit« zu finden. Der Brauchbarkeit der angegebenen Kriterien müssen wir mit Skepsis gegenüberstehen wegen der Vieldeutigkeit der in ihnen auftretenden Termini. Geschwindigkeiten zum Beispiel lassen sich einerseits als zusammensetzbar und zerlegbar auffassen, wie wir soeben sahen; wenn aber anderseits jemand behauptete, jede müsse eigentlich als ein unteilbares »Ganzes« angesehen werden, da sich doch nicht wirklich Teile an ihr unterscheiden ließen, so kann man ihn nicht widerlegen, sondern seine Redeweise höchstens als unpraktisch erklären.

Die Frage: Summe oder Ganzheit? scheint keine Tatsachenfrage, sondern eine Angelegenheit der willkürlichen Festsetzung zu sein. In dieser Vermutung werden wir bestärkt durch den Streit darüber, ob echte Ganzheiten oder Gestalten auch im Gebiete der Physik vorkommen. W. Koehler bejaht diese Frage, indem er eine Reihe von Fällen angibt, in denen die Ganzheitskriterien zutreffen, zum Beispiel die Verteilung der Elektrizität auf einem beliebig gestalteten Leiter, für die ein bestimmter Gleichgewichtszustand charakteristisch ist, der sich nach jeder Störung von selbst wieder herstellt.

Driesch hat gegen Koehler eingewendet (Annalen der Philosophie, V, 1), daß »physikalische Gestalten« niemals echte Ganzheiten seien, sondern nur »Wirkungseinheiten«. Freilich seien sie keine bloßen Summen in dem Sinne, daß das System als Ganzes sich nicht änderte, wenn man einen seiner Teile wegnimmt oder verschiebt; aber das komme eben daher, daß die einzelnen Teile ganz bestimmte Wirkungen aufeinander ausüben. Kenne man das elementare Gesetz des Wirkens der Teile, so könne man alles voraussagen, was sich an dem System abspielen wird; das Verhalten des Ganzen sei aus dem der Teile ableitbar, wenn man nur die äußeren Sonderbedingungen kenne, unter denen das System steht. In jenem Falle der Elektrizitätsverteilung zum Beispiel seien diese Bedingungen durch die Form des Leiters gegeben: diese sei oft eine klare Ganzheit, aber nur deshalb, weil sie »Intelligenzprodukt«, »vom Physiker gemacht« sei.

Lassen wir den letzten Gedanken beiseite, weil er offenbar nur Verwirrung stiften kann (denn er läuft darauf hinaus, die Einfachheit oder Symmetrie geometrischer Formen zum Kriterium der Ganzheit zu erheben, wonach aber auch nicht von Physikern gemachte Gebilde, wie Sterne, Sonnensysteme, Kristalle, als Ganzheiten angesehen werden müßten, gewiß gegen Drieschs Absicht), so laufen diese Ausführungen darauf hinaus, daß die alten Ganzheitskriterien als unzureichend erklärt und neue aufgestellt werden. Wenn Driesch hervorhebt, daß Physik und Chemie ihre Gebilde niemals als reine »Und-Verbindungen« beschreiben, sondern stets als Wirkungseinheiten aufgefaßt hätten, so muß man ihm darin vollständig recht geben – falls nämlich die Bedeutung des Wortes »Und-Verbindung« die sein soll, daß es jede Wechselwirkung zwischen den Teilen ausschließt. Wenn »Wirkungseinheiten« schon »Ganzheiten« wären, so gäbe es – dies scheint Driesch sagen zu wollen – in der Natur überhaupt nur Ganzheiten; welche Kriterien schlägt er nun vor, um beide zu trennen?

Der auch sonst oft geäußerte Gedanke, bei einem echten Ganzen dürfe sein Verhalten nicht aus dem seiner Teile »ableitbar« sein, kann gewiß nicht so verstanden werden, daß Ganzheitsprozesse überhaupt nicht naturgesetzlich berechenbar seien (denn das würde Identifikation solcher Prozesse mit nichtdeterminiertem, zufallsmäßigem Geschehen bedeuten), sondern er meint offenbar – und diese Formulierung hört man sehr oft –, daß das Verhalten der Teile durch das Ganze bestimmt werde, nicht aber umgekehrt. Aber dieser Gedanke beruht, wie so viele andere Versuche, die Lebensvorgänge vor den anorganischen auszuzeichnen, auf völligem Mißverstehen der Begriffe »Gesetz«, »Kausalität«, »Bestimmen« Vgl. die Ausführungen des Verfassers über das »Kausalprinzip in der gegenwärtigen Physik«, dieses Buch, S. 3 ff.. Wenn die Gesetzmäßigkeit der Teile durch die des Ganzen ausgedrückt werden kann, so ist stets auch das Umgekehrte der Fall; es handelt sich um einen bloßen Unterschied der Schreibweise. Der Laie wird dies am leichtesten erkennen, wenn er darauf aufmerksam gemacht wird, daß das Ganze nur dann vorhanden ist, wenn alle seine Teile vorhanden sind, daß daher die Aussage, irgendein Geschehen werde durch das Ganze bestimmt, gleichbedeutend ist mit der Aussage, es werde durch alle seine Teile und deren Beziehungen untereinander bestimmt. Wenigstens gilt dies, so lange man unter Ganzheit etwas empirisch Feststellbares versteht, und wollte man dies nicht, so würde jede Verständigungsmöglichkeit aufhören, es gäbe keine Diskussion.

Das zweite in den oben angeführten Bemerkungen von Driesch vorgeschlagene Kriterium würde besagen, daß den organischen Strukturen ihre Ganzheit von außen, nämlich durch die gegebene physische Form, aufgeprägt sei, während sie bei lebendigen Wesen aus dem Innern stamme und sich daher nach äußeren Störungen in weiten Grenzen von selbst wiederherstelle (z. B. bei Regenerationsprozessen). Auch dies führt zu keiner scharfen Trennung; denn einerseits spielen äußere Bedingungen auch im Organischen eine niemals ganz zu vernachlässigende, oft durchaus entscheidende Rolle, und anderseits kommt Gestaltung und Ausbildung bestimmter Randbedingungen auch im Anorganischen vor, wie in den bereits erwähnten Fällen des Sonnensystems oder des Kristallwachstums. Für den Fall der »homogenen Tropfenbildung« gibt Driesch dies selbst zu, meint jedoch, daß dergleichen »sehr einfache spezifische Fälle als Analogien für das Biologische gar nicht in Frage« kämen. Warum kommen sie nicht in Frage? Nur weil sie einfach, die Organismen aber kompliziert sind? Dann läge der Unterschied zwischen echten Gestalten und physikalischen Gebilden nur in der Komplikation, wäre also rein graduell und folglich unscharf und willkürlich. Ein anderer Grund, warum keine Analogien vorliegen sollen, ist weder angegeben noch ersichtlich, und so werden wir in unserer Meinung bestärkt, daß es sich beim Gebrauch der Termini »summativ« und »ganzheitlich« gar nicht um eine rein objektive Charakterisierung der mit diesen Adjektiven belegten Gebilde handelt, sondern um eine Verschiedenheit der Beschreibung, der Erkenntnismittel, an denen stets etwas Willkürliches ist. Denn die Darstellung unserer Erkenntnisse hängt nicht nur ab von den Eigenschaften der erkannten Dinge, sondern auch von der Art der verwendeten Darstellungsmittel, welche mehr oder weniger zweckmäßig sein können.

Die Richtigkeit unserer Vermutung wird durch eine genauere Betrachtung der Sachlage bestätigt. Den Schriftstellern, die von einer »additiven« oder »summativen« Zusammensetzung sprechen, schwebt ohne Zweifel so etwas vor wie das Verfahren der klassischen Physik (dessen universale Anwendbarkeit freilich durch die neueste Entwicklung der Naturforschung in Frage gestellt ist). Es besteht darin, daß man sich das zur Beobachtung stehende Gebilde in zahllose sehr kleine Elementarbezirke Volumelemente) zerlegt denkt und seinen Gesamtzustand darstellt, indem man den physikalischen Zustand jedes einzelnen Elements vollständig angibt. Man kann stets sagen, das ganze Gebilde sei aus diesen kleinen Elementarvolumina »zusammengesetzt« – unbekümmert darum, ob diese aufeinander wirken und nach welchem Gesetz. Sofern man sich auf das Beobachtbare beschränkt, ist diese Betrachtungsweise stets möglich, bei jedem Organismus so gut wie bei einem unbelebten System, denn es liegt im Wesen der Beobachtung, daß alles Wahrgenommene räumlich und zeitlich bestimmt ist. Daher ist die Angabe alles dessen, was in jedem Raumteilchen eines Gebildes sich zu jeder Zeit ereignet, die vollständige Angabe des beobachtbaren Gesamtgeschehens in ihm. (Wir wissen heute, daß die Raum-Zeitbeschreibung für submikroskopische, atomare Dimensionen nicht ohne weiteres anwendbar ist, aber das ist hier nicht wichtig, da es für gestaltete und ungestaltete, organische und anorganische Gebilde gleichermaßen gilt; der Unterschied zwischen ihnen liegt ja im beobachtbaren Verhalten.)

Die vollständige Beschreibung des Verhaltens aller Teilchen eines Systems enthält bereits die lückenlose Beschreibung seines Gesamtverhaltens; die Gesetze des Geschehens in ihm sind nicht etwas, das zu der Beschreibung hinzukommen muß, sondern etwas, das aus ihr abzulesen ist. Dies geschieht dadurch, daß man die zahllosen Einzelbeschreibungen mit Hilfe möglichst einfacher Formeln auszudrücken sucht, durch die im Falle des Gelingens alles wundersam geordnet erscheint. Aufstellung von Naturgesetzen, das heißt Erklärung von Naturerscheinungen, ist nichts anderes als eine solche Vereinfachung vorliegender Beschreibungen, eine Zusammenfassung vieler mit Hilfe weniger Formeln oder Funktionen.

Die Gesetze werden entweder in mathematischer oder in loserer Form aufgestellt; im ersteren Falle können die dabei verwendeten Funktionen von verschiedenster Gestalt sein, keine ist von vornherein bevorzugt. Es ist für eine physikalische »Erklärung« durchaus nicht erforderlich, die Beschreibung der Vorgänge etwa durch von Punkt zu Punkt wirkende Kräfte durchzuführen (wie noch Helmholtz zuerst glaubte), oder durch Nahewirkungsgesetze (Differentialgleichungen einer Feldtheorie), sondern ganz andere Formen sind prinzipiell gleichberechtigt: es könnten zum Beispiel zeitliche Fernwirkungen angenommen werden, oder auch Abhängigkeiten von der Art, daß das Eintreten eines Ereignisses an den Ablauf eines bestimmten über endliche Zeiten und Räume sich erstreckenden Vorganges geknüpft wäre (in diesem Falle könnte man schon von »Ganzheitskausalität« sprechen).

Für uns ist wichtig, daß die Zusammenfassung der Einzelbeschreibungen prinzipiell willkürlich ist: nur die Rücksicht auf Einfachheit und Bequemlichkeit ist für die Wahl der Ordnung entscheidend. Hat man es z. B. mit einem Wirbelfaden in einer Flüssigkeit zu tun, so wird es bequem sein, die allgemeine Beschreibung der Vorgänge in der Flüssigkeit, welche darin besteht, daß man die Lage und Geschwindigkeit jedes Teilchens zu jeder Zeit angibt, dadurch zu vereinfachen, daß man die den Wirbelfaden bildenden Teilchen zusammenfaßt, also Beziehungen aufsucht, die gerade nur für diese Teilchen gelten. (Man findet z. B., daß das Produkt aus Querschnitt und Rotationsgeschwindigkeit für jeden Wirbelfaden konstant ist.) Man wird also ein solches Gebilde, wie einen Wirbelfaden, als eine »Individualität«, als ein »Ganzes« betrachten und etwa die Gesamtbewegung der Flüssigkeit dadurch charakterisieren, daß man die Bewegungen der einzelnen Wirbelfäden verfolgt. – An diesem Beispiel mag klar werden, was ganz allgemein gilt: Eine »ganzheitliche« Beschreibungsweise wird nirgends die einzig mögliche, aber immer dort am Platze, ja oft praktisch allein durchführbar sein, wo gewisse »Invarianten« auftreten, gewisse Anordnungen oder Kombinationen, die im Wechsel des Geschehens erhalten bleiben, indem sie bestimmte sinnlich auffällige Eigenschaften, wie besonders die Raumform und die Art des räumlichen Zusammenhanges der Teile bewahren.

Solche Invarianten treten nun immer an belebten Körpern auf und bestimmen ihre charakteristische Eigenart; alle organische »Zweckmäßigkeit« besteht eben darin, daß eine gewisse Gesetzmäßigkeit aller Teilvorgänge durch diese Invarianten ausgedrückt werden kann. Eine menschliche Hand zum Beispiel behält von der Geburt bis zum Tode des Individuums durch alle Zufälligkeiten des Stoffwechsels und des Lebenslaufs hindurch ihre Form im großen ganzen bei: sie hat immer fünf Finger, die mit Nägeln versehen sind, eine bestimmte relative Länge und Beweglichkeit besitzen, nach kleinen Verwundungen zuheilen usw. Erst nach dem Tode löst sich die Gestalt durch Verwesung auf. Der ganze Leib des Lebewesens, jedes Organ daran, jede Zelle, jeder Zellkern, jedes Gen kann als Ganzheit betrachtet werden, weil es eine Invariante in dem erklärten Sinne darstellt.

Ebenso wie es etwa in der Astronomie selbstverständlich ist, daß man die zu einem Planeten gehörenden Materieteilchen zusammenfaßt als einen Himmelskörper bildend, den man dann als Ganzes mit einem Namen belegt; oder wie es natürlich ist, den Zustand einer von Wirbellinien durchzogenen Flüssigkeit durch die Bewegung eben dieser Linien zu beschreiben, ebenso versteht es sich von selbst, daß man bei der Beschreibung und Erklärung organischer Vorgänge von Organen spricht, von Nerven, Augen, Knochen, Gliedern, Zellen, nicht aber etwa bloß von den Molekülen, aus denen diese Dinge bestehen. Diese natürliche Beschreibungsart und Sprechweise hochtönend als eine besondere, nämlich als »organismische« Auffassung des Lebens zu charakterisieren, scheint mir, milde ausgedrückt, ein terminologischer Fehlgriff zu sein.

Prinzipiell bleibt es auch bei jedem Organismus möglich, alles, was überhaupt über ihn gesagt werden kann, in der Weise zu sagen, daß man allein von den Teilchen spricht, die ihn aufbauen, und von deren Beziehungen zueinander. De facto mag dies nicht angängig sein – ja, beim gegenwärtigen Stande des Wissens ist es sicherlich ausgeschlossen, weil uns der Zustand aller Teilchen nicht bekannt ist – das ändert aber nichts an der Einsicht, daß Organismen auch einer »summativen« Beschreibung zugänglich sind (wenn man sie so nennen will), und daß es keineswegs in ihrem Wesen liegt, die »ganzheitliche« Darstellung als einzig mögliche zu fordern.

Umgekehrt gilt, daß es auch keine Gebilde gibt, deren Verhalten prinzipiell nur beschrieben werden könnte, indem man von jedem Teilchen einzeln redet, sondern man kann stets willkürlich Gruppenbildungen vornehmen und diese wie »Ganze« behandeln; aber das kann sehr unpraktisch sein, weil es in den meisten Fällen nur zu größeren Komplikationen führt. Wir haben aber Beispiele von anorganischen Gebilden kennengelernt, in denen es höchst vorteilhaft ist. Ein neues Beispiel würde uns etwa die meteorologische Behandlung der atmosphärischen Erscheinungen liefern: dort ist es, genau wie bei Organismen, praktisch unmöglich, die Bewegung jedes einzelnen Luftteilchens oder Wassertröpfchens zu verfolgen; statt dessen betrachtet man Gruppen von ganzheitlichem, invariantenhaftem Charakter, wie Depressionen, Zyklone, Gewitter usw.

Streng genommen ist es niemals korrekt, von einem Gebilde zu sagen, es sei eine »bloße Summe« oder eine »Ganzheit«, sondern man meint: bei diesem Gebilde ist eine summenhafte, bei jenem eine ganzheitliche Begriffsbildung zum Zwecke der Erkenntnis vorteilhafter. Ein genaues Analogon zu dieser Situation findet sich innerhalb der physikalischen Naturbeschreibung: es wäre sinnlos, vom Raume der Physik einfach zu sagen, er sei »euklidisch« oder »nichteuklidisch«, sondern es muß heißen: »es ist einfacher, ihn auf euklidische – bzw. nichteuklidische Weise zu beschreiben«. Möglich ist stets beides, und erst dadurch, daß man bestimmte Definitionen einführt, entscheidet man sich für das eine oder das andere. Die nähere Durchführung dieses Analogons wäre sehr lehrreich und würde viel Licht auf die Fehler werfen, die in der Behandlung unserer Frage häufig begangen werden. Es handelt sich um typische Mißverständnisse, die im Grunde bei jeder erkenntnistheoretischen Frage wiederkehren: Probleme der passenden Beschreibung, der zweckmäßigen Definitionen werden mit Tatsachenfragen verwechselt, und so entstehen scheinbar ontologische Probleme, metaphysische Streitfragen. Die »Ganzheit«, ein vortreffliches begriffliches Beschreibungsmittel, verwandelt sich in ein metaphysisches Wesen, wird zur »Entelechie« und ähnlichen Ausgeburten philosophischer Unklarheit.

Die Anwendung unseres Resultates auf das Problem Individuum-Gemeinschaft ist leicht. Es ist vollkommen klar, daß alle Aussagen über Völker, Staaten, Parteien, über Recht, Sitte usw. aufgefaßt werden können als Aussagen über die Individuen, die jenen Gemeinschaften angehören oder Träger jener Sitten usw. sind. Wenn einer genau wüßte, was alle menschlichen Individuen auf der Erde getan oder gesagt haben, so würde er alles wissen, was die Geschichte und Soziologie lehren können. Was sich über Nationen, Kasten oder sonstige »höhere Einheiten« sagen läßt, wäre in seinem Wissen restlos enthalten; alle wahren Sätze über derartige Ganzheiten ließen sich aus den Sätzen über Individuen ableiten, sie würden nicht zu diesen als neue unabhängige Wahrheiten hinzukommen. Anderseits ist klar, daß diese »summative« Darstellungsweise für den Historiker höchst unpraktisch wäre: selbst wenn er die Taten jedes Individuums bis ins einzelne verfolgen könnte, würde er es doch nicht tun, sondern fortfahren, vom »Willen des Volkes«, vom »Charakter der Nationen«, vom »Streit der Stände« usw. zu sprechen, aber es wäre ein primitives philosophisches Mißverständnis, zu glauben, daß damit die Existenz höherer Wesenheiten, wie Volkswille, Nation, Stand, behauptet würde, von denen allein die Geschichte handle. Es ist nur eine bequeme Sprechweise eingeführt, in der sich die Vorgänge, die uns interessieren, übersichtlich darstellen lassen. Hier, wie auf allen anderen Gebieten, ist der Satz, daß das Ganze den Teilen logisch vorausgehe, eine leere Phrase.

Was endlich die psychologische Begriffsbildung betrifft, so scheint es mir zweifellos, daß eine »ganzheitliche« Darstellungsweise, wie sie von der »Gestaltpsychologie« befürwortet wird, die einzig aussichtsreiche ist, das heißt, nur mit ihrer Hilfe gelingt es praktisch, zu einer Formulierung der Gesetzmäßigkeiten zu gelangen, die den Gegenstand der Psychologie bilden. Aber auch hier wäre es unrichtig, den Grundgedanken der Gestaltpsychologie so auszusprechen, daß die psychischen Gebilde eben Gestalten sind, daß eine zerlegende und zusammensetzende Betrachtung nicht durchgeführt werden könne und dürfe. Prinzipiell ist es vielmehr auch bei allen psychischen Gebilden möglich, sie als aus Teilen zusammengesetzt aufzufassen; nur muß man vorher genau definieren, was man eigentlich unter einem »Teil« verstehen will. Ob man beim Hören eines Tones die Obertöne als »Teile« des akustischen Phänomens, ob man bei einer Schmerzempfindung die zeitlich aufeinanderfolgenden Phasen des Schmerzes als dessen »Teile« bezeichnen will, das ist lediglich Sache der Definition. Hier drängen sich bestimmte Festsetzungen nicht in gleichem Maße als natürlich auf, wie bei physischen Gebilden die räumliche Zerlegung, und die grotesken Mißgriffe der alten »atomistischen« Psychologie rühren gerade daher, daß man Erklärungen nach dem äußerlichen Vorbilde der räumlich-zeitlichen Zusammensetzung zu geben suchte, ohne sich vorher über den Begriff des Teiles klargeworden zu sein. Man teilte gedankenlos, wie es einem gerade einfiel, zum Beispiel in »Vorstellungen«, und ordnete in physiologischen Theorien solche Teile naiv den räumlichen Teilen des Gehirns zu, also einzelne Vorstellungen einzelnen Nervenzellen. Mit solchen Dingen hat die Gestaltstheorie gründlich aufgeräumt. Aber auch für sie kann der Gegensatz von »Summe« und »Ganzheit« nicht den Gegensatz zweier Arten von Dingen oder Vorgängen bedeuten, sondern er bleibt ein Gegensatz zweier Darstellungsweisen.

Inhalt

Über den Begriff der Ganzheit.