Autoren

∞

Werke

∞

Neu

∞

Information

∞

Shop

∞

Lesetips

∞

Textquelle

∞

Spezielle Relativitätstheorie.

2. Die neuen Tatsachen.

a) Der Fizeau-Versuch.

Wir stehen hier nicht nur vor sehr interessanten, sondern auch vor enorm schwierigen Fragen. Schon die Vorfrage nach der Lichtgeschwindigkeit überhaupt, ganz gleich ob im ruhenden oder im bewegten System, erfordert zu ihrer Beantwortung einen außerordentlichen Scharfsinn in der Versuchsanordnung und zugleich die allergrößte Genauigkeit und Sorgfalt in der praktischen Ausführung. Es ist nun sogar durch verschiedene voneinander unabhängige, sowohl astronomische als auch physikalische Methoden gelungen, die Fortpflanzungsgeschwindigkeit des Lichtes mit erstaunlicher Genauigkeit zu bestimmen. Sie beträgt bekanntlich ziemlich genau 300 000 km in der Sekunde; das Licht braucht also für die Strecke Köln–Königsberg genau 1/300 Sekunde, würde den Erddurchmesser in noch nicht 1/20 Sekunde durchqueren und eilt von der Erde bis zum Mond in noch nicht 1½ Sekunden. Es erscheint auf den ersten Blick ganz ausgeschlossen, festzustellen, ob und wie sich diese enorme Geschwindigkeit von den vergleichsweise ganz winzigen irdischen Geschwindigkeiten beeinflussen läßt. Beträgt doch selbst die Geschwindigkeit des schnellsten Geschosses in dem Augenblick, wo es die Mündung des Laufes verläßt, nur knapp 1 km in der Sekunde, um dann sehr schnell abzunehmen.

In der Tat würde die Lösung unseres experimentellen Problems nicht gelungen sein, wenn uns nicht hierfür eine ganz außerordentlich empfindliche Methode zur Verfügung stände. Es ist die sogenannte Interferenzmethode, die darin besteht, Lichtgeschwindigkeiten nicht etwa absolut zu messen, sondern nur zwei verschiedene miteinander zu vergleichen. Das Licht ist bekanntlich eine Wellenbewegung, die einzelnen Wellen sind außerordentlich klein, auf das Millimeter gehen etwa 2000, je nach der Farbe etwas mehr oder weniger. Wenn wir uns nun auch von dem inneren Mechanismus des Lichtvorganges und der Lichtfortpflanzung keine anschauliche Vorstellung zu machen vermögen, so wissen wir doch, daß er alle Eigentümlichkeiten der Wellenbewegung hat, daß sich insbesondere zwei Lichtstrahlen verstärken oder addieren, wenn immer Wellenberg des einen auf Wellenberg des andern und Wellental des einen auf Wellental des andern fällt, daß sie sich aber aufheben, also Dunkelheit erzeugen, wenn Wellenberg des einen auf Wellental des andern fällt. Teilt man nun, was durch einfache optische Hilfsmittel gelingt, einen Lichtstrahl in zwei Arme, die man etwa parallel miteinander eine Wegstrecke hergehen läßt, um sie dann wieder zu vereinigen, so wird, falls die beiden getrennten Lichtstrecken wirklich genau gleich lang waren, der erste der eben genannten Fälle eintreten, beide Strahlen werden sich verstärken, das nun entstandene Licht wird genau so hell sein, als es auch ohne Trennung in zwei Teile gewesen wäre. Verlangsamen wir nun aber, z. B. durch ganz geringfügige Verlängerung des Weges oder auch sonstwie, die Lichtbewegung in dem einen Arm, während sie in dem andern ganz ungeändert bleiben möge, so wird nicht mehr genau Wellenberg auf Wellenberg und Wellental auf Wellental fallen, es wird vielmehr eine Verschiebung eintreten, und diese läßt sich stets so groß bemessen, daß nun Wellenberg auf Wellental fällt, also Dunkelheit eintritt. Man nennt dies »Interferenz«. Die außerordentliche Größe der Lichtgeschwindigkeit und die winzige Kleinheit einer Lichtwelle bedingt nun, wie leicht zu sehen, eine geradezu unerhört kurze Dauer einer solchen Lichtschwingung, das Licht schwingt in einer Sekunde mehrere hundert Billionen mal, und wenn bei unserm eben erwähnten Versuch sich die Zeit, die das Licht zu der einen der beiden parallel gehenden Strecken braucht, auch nur um eine tausend Billiontel (1 mit 15 Nullen!) Sekunde ändert, so würde sich dies deutlich durch die »Interferenz« bemerkbar machen. Natürlich haben wir hiermit nur die allergröbsten Umrisse der Methode wiedergegeben.

Auf diesem Wege versuchte nun zuerst der berühmte französische Physiker Fizeau im Jahre 1851 den Einfluß zu bestimmen, den die Bewegung des Mittels auf die Lichtgeschwindigkeit hat. Er ließ Wasser oder Luft in eine Röhre strömen und verglich die Geschwindigkeit der Lichtfortpflanzung, wenn sie im Sinne der strömenden Luft erfolgt, mit der in ruhender Luft oder mit der im entgegengesetzten Sinne bewegten. Auf die Versuchsergebnisse mit Wasser, in dem die Lichtgeschwindigkeit ohnehin eine ganz wesentlich andere ist als in Luft, und wo noch mancherlei sonst zu berücksichtigen ist, wollen wir hier nicht näher eingehen, für Luft jedoch ergab der Versuch mit voller Sicherheit: Die Bewegung der Luft, in der sich Licht fortpflanzt, hat nicht den geringsten Einfluß auf diesen Vorgang. Ob sich Licht bewegt in einer Luft, die im Sinne der Lichtbewegung strömt, oder im entgegengesetzten, oder ob sie gar nicht strömt, das Licht bewegt sich deswegen noch nicht um den tausendsten Teil einer Billiontel Sekunde schneller oder langsamer; es läßt sich anscheinend nicht im geringsten von den Bewegungen seiner Umwelt stören. Erinnern wir uns des eben gebrauchten Beispiels von der Ball- und der Schallbewegung auf dem fahrenden Schiff, so können wir also sagen: Das Licht bewegt sich keineswegs so wie der geworfene Ball, der an der Bewegung des Schiffes selbst teilnimmt und folglich, vom Ufer aus beurteilt, sich schneller zu bewegen scheint, wenn seine Bewegung mit der des Schiffes zusammenfällt, langsamer, wenn sie entgegengesetzt ist. Es verhält sich vielmehr genau so wie der Schall, der, wenn auch auf dem Schiffe erzeugt, doch keineswegs die Bewegung des Schiffes mitmacht, sondern sich, vom Ufer aus beurteilt, mit der gleichen Geschwindigkeit in der einen und in der andern Richtung bewegt. Im Anschluß an unsere frühere Ausdrucksweise können wir daher auch sagen: Untersuchen wir die Lichtbewegung in einem bewegten System von einem festgebliebenen System aus, so gehört die Lichtbewegung selber zum festen System.

b) Der Michelson-Versuch.

Das eben besprochene Ergebnis des Fizeau-Versuchs ist die unmittelbare Veranlassung zur Stellung einer neuen Aufgabe, nämlich der Untersuchung der Lichtbewegung durch das bewegte Mittel vom bewegten System aus. Hier müßte doch nun ein Einfluß der Bewegung zu erwarten sein, ganz entsprechend dem Einfluß, den die Schiffsbewegung auf die Fortpflanzung des Schalles hat, wenn dieser Vorgang nicht mit dem feststehenden Ufer, sondern mit dem Schiff selber verglichen wird. Denken wir uns also etwa einen Beobachter, der in die Röhren des Fizeau-Versuchs hineinkriecht und dort zugleich mit der bewegten Luft fortgeblasen wird. Der Mann sei so winzig klein, daß er auch die Röhrenwandungen nicht bemerkt, an denen er seine Fortbewegung etwa vergleichen und feststellen könnte, seine ganze ihm zugängliche Umwelt bewegt sich also im Luftstrom genau wie er, er wird sich also selbst für ruhend halten. Dieser Mann stelle jetzt die Geschwindigkeit eines durch seine Luft hindurchgesandten Lichtstrahls fest. Vergegenwärtigen wir uns nun: Ob der Lichtstrahl zu einem bestimmten Zeitpunkt an einem bestimmten Punkt angelangt ist oder nicht, ist ganz zweifellos eine absolut objektive Frage, die, wo und wie sich der Beobachter auch befinden möge, unter gar keinen Umständen eine verschiedene Beantwortung finden kann. Da sich nun der Beobachter während der Ausbreitung des Lichtes selbst weiterbewegt hat, so wird er also, diese Folgerung scheint ganz unausweichlich zu sein, in seiner eigenen, ihm vielleicht selbst vorerst noch unbekannten Richtung eine geringere Geschwindigkeit des Lichtes feststellen müssen, als in der entgegengesetzten oder in einer seitlichen Richtung. Und er wird hierdurch imstande sein, Größe und Richtung seiner Bewegung festzustellen, oder sagen wir vielleicht noch deutlicher: Größe und Richtung seiner Bewegung festzustellen im Vergleich oder »relativ« zu demjenigen System, in dem sich das Licht bewegt.

Wir beabsichtigen nicht, die Versuchsanordnung des Michelson-Versuchs im einzelnen zu schildern, da dies einige wenngleich sehr einfache mathematische Kenntnisse voraussetzt und übrigens oft genug in populären Schriften bereits geschehen ist, wo der mehr verlangende Leser nachlesen kann. Wir bemerken nur folgendes: Es war deshalb schwierig, eine zweckdienliche Anordnung zu finden, weil die Endpunkte der Strecke, die das Licht im Sinne der Luftbewegung und im entgegengesetzten durchlaufen soll, nicht zusammenfallen werden, die Interferenzmethode aber, wie wir wissen, durchaus die Vereinigung der getrennten Lichtstrahlen verlangt. Zwar gelang es, durch höchst geistvolle geometrische Anordnung diese Schwierigkeit zu überwinden, aber doch nur auf Kosten der Größe des zu erwartenden Versuchsergebnisses. Um überhaupt noch ein meßbares Versuchsergebnis zu erhalten, mußte daher für die Bewegung des Mittels eine sehr viel schnellere ausfindig gemacht werden, als sie für den Fizeau-Versuch zur Verfügung stand; die schnellste uns zugängliche materielle Bewegung aber ist die fortschreitende Bewegung der Erde, die 30 km in der Sekunde beträgt, was freilich auch erst den zehntausendsten Teil der Lichtgeschwindigkeit ausmacht.

Michelson wählte also zur Vergleichsbewegung die der Erde, die sich auch wegen des großen sonstigen Interesses, das sich an sie knüpft, ohnehin empfohlen hätte. Er stellte sich die Frage: Bewegt sich, natürlich vom mitbewegten Beobachter aus beurteilt, das Licht schneller im Sinne der Erdbewegung oder im entgegengesetzten? Und wieviel beträgt der Unterschied? Es leuchtet ein, wie ungeheuer interessant eine Lösung der Aufgabe auch etwa vom astronomischen Standpunkt aus gewesen wäre. Wir kennen die Bewegung der Erde relativ zur Sonne; aber die Bewegung der Sonne im Fixsternraum, also dem Weltenraum, kennen wir nur höchst unvollkommen, und es ist nach dem heutigen Stand der Astronomie auch zu erwarten, daß es noch sehr lange, vielleicht Jahrhunderte lang fortgesetzter Beobachtungen bedürfen wird, ehe sich diese Frage befriedigend, oder wenigstens befriedigender als heute, wird lösen lassen. Der Michelson-Versuch schien die Aussicht zu bieten, das wichtige und schwierige Problem mit einem Schlage zu erledigen; und dies rechtfertigt den außerordentlich großen Aufwand und die noch größere Sorgfalt, die auf den Michelson-Versuch verwandt worden sind.

Was das Relativitätsprinzip anlangt, so hätte man ein Gelingen des Michelson-Versuchs nicht gerade als seine Widerlegung aufzufassen brauchen. Denn so gut wir in dem nun schon öfters erwähnten Vergleichsbeispiel die Geschwindigkeit des Schiffes nicht absolut, sondern nur relativ zu dem System, in dem sich der Schall bewegt, nämlich der Luft, feststellen konnten, genau so gut hätte auch der Michelson-Versuch nicht die absolute Bewegung der Erde ergeben, sondern nur ihre relative, relativ nämlich zu dem System, in dem die Lichtbewegung erfolgt, also zum Äther. Dies wäre jedoch nur mehr eine rein theoretische, grundsätzliche Auffassung gewesen zur Rettung der Relativität um jeden Preis. Der Äther, wenn wir ihn schon als die unumgängliche Voraussetzung für die Fortpflanzung des Lichtes annehmen wollen, erfüllt ja die ganze, unsern Sinnen zugängliche Welt bis in die fernsten Tiefen des Fixsternhimmels. Eine Bewegung, relativ zum Äther, mag sich philosophisch genommen von einer Bewegung gegen den leeren Raum unterscheiden, in praktischer, namentlich experimentell-physikalischer Hinsicht wäre jedoch dieser Unterschied nicht greifbar gewesen. Ein Gelingen des Michelson-Versuchs hätte also nur eine höchst platonische Rettung der Relativität gestattet.

Und nun endlich das Ergebnis des 1881 zuerst angestellten und 1887 mit noch größerer Genauigkeit wiederholten Michelson-Versuchs? Es war völlig negativ. Michelson verglich mit seinem so genauen Apparat die Lichtgeschwindigkeit in allen möglichen Richtungen, in keiner fand er auch nur den allergeringsten Unterschied. Der Versuch wurde zu andern Jahreszeiten wiederholt, wenn also die Bewegung der Erde gegen den Fixsternhimmel eine andere Richtung hatte, vergeblich! Und an der Bewegung der Erde um die Sonne ist doch im Ernst nicht zu zweifeln! Sollte man nun auch annehmen, daß vielleicht durch eine Bewegung der Sonne und mit ihr des ganzen Planetensystems, die der Erdbewegung entgegengesetzt, aber gleich schnell sei, die Bewegung der Erde sozusagen aufgehoben werde, so daß diese im Fixsternraum stillstehe, so könnte dies doch nur für eine einzige Jahreszeit gelten, das Mißlingen des Michelson-Versuchs also auf die Dauer nicht erklären.

Der Michelson-Versuch ist mit so großer Genauigkeit angestellt, daß, wäre das Ergebnis auch nur 1/100 des erwarteten gewesen, es nicht hätte verborgen bleiben können. Zusammenfassend und im Anschluß an unsere frühere Ausdrucksweise können wir das Ergebnis des Michelson-Versuchs so aussprechen: Untersuchen wir die Lichtbewegung in einem bewegten Mittel vom bewegten System aus, so gehört die Lichtbewegung selber auch zum bewegten System.

c) Konfrontation.

Vergleichen wir die Ergebnisse beider Versuche, so springt der Widerspruch sofort in die Augen, und wir werden ihn sogleich in noch etwas helleres Licht rücken. Zuvor jedoch müssen wir einen möglichen, auch tatsächlich oft erhobenen Einwand besprechen. Man könnte nämlich sagen: Die Analogie zwischen den beiden Versuchen ist keine vollkommene; denn beim Fizeau-Versuch stammt das Licht von einer Lichtquelle in dem als fest angenommenen System, beim Michelson-Versuch ist die Lichtquelle mitbewegt. In der Tat wird im ersten Falle das Licht von außen in die Röhren hineingesandt, an der Bewegung des Mediums in den Röhren hat es keinen Anteil. Beim Michelson-Versuch wird nicht das Licht von außen in das bewegte System, das ja hier die ganze Erde ist, hineingeschickt, sondern vielmehr auf der Erde, also auf dem bewegten System selber erzeugt. Man könnte etwa daran denken, Fixsternlicht zu diesem Versuch zu benutzen, da dieses ja ganz sicher von außen her in das System gelangt; indessen ist dieses natürlich zu schwach zur Anstellung solch feiner Versuche. Beim Sonnenlicht hätte man wieder die Schwierigkeit, daß es nur in einer einzigen Richtung, nämlich senkrecht zur Bewegung, wirken könnte, während beim Fizeau-Versuch die beiden Bewegungsrichtungen, die des Lichtes und die des Systems, hier des Luftstroms, zusammenfallen.

Aber diese ganze Sorge ist wohl unnötig. Es ist nicht anzunehmen, daß eine Bewegung der Lichtquelle irgendeinen Einfluß auf die Lichtfortpflanzung ausübt. Dies wäre schon theoretisch recht schwierig vorzustellen. Denn immer mehr hat sich namentlich seit Faraday die Meinung vom Ausschluß jeder Fernwirkung, insbesondere bei elektrischen und elektromagnetischen Vorgängen, zu welch letzteren ja auch das Licht gehört, und von der alleinigen Geltung der Nahewirkung festgesetzt. Nicht die vielleicht weit entfernte Lichtquelle, sondern der Zustand auf dem unmittelbar vorangegangenen Strahlteil ist die Ursache der Lichtwirkung auf dem folgenden. Demnach müßte der Lichtvorgang in einem Teilchen selbst verschieden sein, um eine verschiedene Wirkung im nächsten auszulösen. Das wäre sehr schwer vorstellbar. Auch die Analogie des Schalles zeigt, daß es nicht den geringsten Einfluß auf die Geschwindigkeit hat, ob der Klang z. B. von einer bewegten oder von einer ruhenden Glocke ausgeht. Aber entscheiden kann natürlich nur die Erfahrung. Und die Erfahrung, insbesondere astronomische Tatsachen sprechen durchaus dafür, daß die etwaige Bewegung der Lichtquelle ohne jeden Einfluß auf die Lichtgeschwindigkeit ist.

Demnach ist der Widerspruch zwischen den beiden grundlegenden Versuchen vollkommen. Machen wir ihn uns etwa an folgender Vorstellung klar: Wir befinden uns am Ufer eines Flusses, an dem auch Eisenbahnen verkehren. Diese fahren stromauf und stromab mit genau derselben Geschwindigkeit. Wir wollen nun annehmen, die Bahnen bewegen sich auf einem im Flusse befindlichen Floß; wird nun immer noch die gleiche Geschwindigkeit nach beiden Richtungen festgestellt, so wird der Beobachter sagen, das Floß ist im Fluß verankert, es steht still. Er wird erwarten, daß wenn er nun in einem kleinen Kahn sich stromab treiben läßt, nunmehr die ihm entgegenkommenden Eisenbahnen schneller an ihm vorbeifahren als die ihn überholenden. Stellt er gleiche Geschwindigkeit fest, so wird er schließen, daß das Floß mit ihm stromab treibt. Nun zeigt der Fizeau-Versuch, wie der auf dem Lande befindliche Beobachter auf ein feststehendes, der Michelson-Versuch, wie der stromab fahrende Beobachter auf ein mitfahrendes Floß schließt. In welchem Bewegungszustande immer der Beobachter sich befinden möge, das Floß, das natürlich nur den mystischen Lichtäther symbolisieren soll, ist relativ zu ihm in Ruhe. Halten wir an seiner Vorstellung fest, so können wir auch sagen: Der Fizeau-Versuch beweist, daß der Äther bei der Bewegung aller Medien in Ruhe bleibt, nicht mitgenommen wird. Der Michelson-Versuch zeigt, daß er in der Tat doch mitgeführt wird. Dies ist übrigens nur eine andere, und zwar gröbere Ausdrucksweise statt der oben gewählten von der Lichtbewegung einmal im festen und das andere Mal im bewegten »System«. Ein zweites Beispiel: Im Augenblick, wo ein langer, sagen wir viele Kilometer langer Eisenbahnzug abfährt, wird am letzten Wagen ein Lichtsignal gegeben. Ob dies auf dem Wagen, etwa auf seinem Dach oder Trittbrett, oder auf dem festen Boden geschieht, ist nach dem Vorigen ganz gleichgültig. Nun wird die Geschwindigkeit gemessen, mit der das Licht sich auf dem Bahndamm und auf dem Zug ausbreitet, sagen wir: der Punkt festgestellt, an dem es nach genau einer Sekunde angelangt ist. Wird auf dem Boden gemessen, so ergibt sich natürlich die Strecke von 300 000 km. Wird aber auf dem Zug gemessen, etwa auf den Trittbrettern, so ergibt sich auch wieder die Strecke von 300 000 km. Und dabei ist, während der Lichtstrahl vorwärts eilte, doch auch der Eisenbahnzug weitergefahren!

Wie man auch die Sache ansehen mag, eines scheint sicher zu sein: Die Systemgeschwindigkeit addiert sich nie zur Lichtgeschwindigkeit und subtrahiert sich nie von ihr, unser obiges Additionstheorem der Geschwindigkeiten (S. 8) gilt nicht für die Lichtbewegung. Und da dieser Satz für die Galileische Auffassung der Relativität wesentlich war, so können wir sagen: Das Galileische Relativitätsprinzip gilt nicht für die Fortpflanzung des Lichtes. Seine allgemeine, absolute Geltung ist damit aufgehoben.

Aber der Widerspruch zwischen den uns bekannten Erfahrungstatsachen ist mit dieser rein negativen Erkenntnis noch nicht geklärt. Dieser heischt gebieterisch eine weitere Untersuchung. Eines aber sehen wir jetzt schon: Der aufgedeckte Widerspruch ist ein derartig greller, die ihn ausmachenden Tatsachen sind von einer so elementaren Wucht, daß seine Beseitigung, mit Verlaub zu sagen, kein Pappenstiel sein kann. Mit sanften Mitteln ist hier nicht auszukommen. Bei der, wie wir hoffen, völlig klargelegten, außerordentlichen Einfachheit der ganzen Sachlage wird es ohne tiefen und unbequemen Eingriff in alte Denkgewohnheiten nicht abgehen. Die einzig bequeme Art, sich mit den Tatsachen abzufinden, nämlich sie nur als solche anzuerkennen, aber auf ihre Deutung, auf ihre Beherrschung von einem geistigen Gesichtspunkte aus, auf eine Einordnung in irgendeine Theorie zu verzichten, welche Methode allerdings Jahrzehnte hindurch geübt wurde, kann und konnte nicht auf die Dauer der Weg der Wissenschaft sein.

3. Die Lorentzsche Deutung.

a) Theorie.

Vorsicht ist der bessere Teil der Tapferkeit, wäre man beinahe versucht zu sagen, wenn man bemerkt, daß mehr als zwei Jahrzehnte ins Land gingen, ehe auch nur ein ernsthafter Versuch gemacht wurde, die im Vorigen dargetane große Schwierigkeit zu heben. Lehrbücher und Vorlesungen über Optik machten über die Fortpflanzung des Lichtes in bewegten Medien nur knappe und nicht eben vielsagende Bemerkungen. Des Michelson-Versuchs, der heute vielleicht der berühmteste aller physikalischen Versuche ist, wurde kaum gedacht. Unter solchen Umständen war es eine ganz außerordentliche Tat des auch sonst hochverdienten niederländischen Physikers H. A. Lorentz, daß er nicht nur die Frage aufgriff und damit den Stein ins Rollen brachte, sondern auch gleich selbst einen ungewöhnlich kühn und großzügig gedachten Lösungsversuch unternahm.

Das Wesentliche seines Gedankens wollen wir uns nun an einem Beispiele klarmachen, das zwar, wie der scharfsinnige Leser vielleicht selbst merken wird, mathematisch nicht ganz korrekt ist, aber, worauf es uns hier in erster Linie ankommt, das Wesentliche in plastischer Deutlichkeit und zugleich sehr leichtverständlich hervortreten läßt. Kehren wir zu unserm fahrenden Eisenbahnzug und zu dem vom Endwagen abgefeuerten Lichtsignal zurück. Lorentz stellt sich vor, daß der Zug eben durch seine Bewegung eine gewisse Verkürzung, eine Kontraktion erleide, und daß ebendies das Schicksal aller bewegten Gegenstände sei. Wie sich alsbald herausstellen wird, darf diese Verkürzung nur als ganz minimal angenommen werden. Aber so geringfügig sie auch sein mag, bemerkt und gemessen werden kann sie überhaupt nur vom festen Boden, dagegen nicht vom Zuge aus. Denn legen wir im Zuge oder auf dem Trittbrett den Maßstab zur Messung an, so zeigt sich, daß dieser, weil er an der Bewegung teilnimmt, sich eben auch verkürzt hat und sich infolgedessen genau so oft auf dem Zuge abtragen läßt, als dies bei ruhendem Zuge der Fall wäre. Die Anzahl Male, die man einen Maßstab an einer Strecke abtragen kann, nennen wir aber die Länge dieser Strecke, sie bleibt natürlich bei gleichzeitiger Verkürzung der Strecke und des Maßstabs ganz ungeändert. Stellen wir uns vor, unser Zug sei 300 000 km lang! Dann wird für den mitfahrenden Beobachter am Ende der ersten Sekunde der Lichtstrahl gerade bei der Lokomotive angelangt sein. Dies sind für ihn, da er seinen Metermaßstab 300 000 000 mal anlegen kann, gerade 300 000 km. Der auf dem festen Boden stehende Beobachter, dessen Maßstab sich ja nicht verkürzt hat, sieht hingegen deutlich, welcher Täuschung sein fahrender Kollege zum Opfer gefallen ist. Für ihn ist der Eisenbahnzug keine 300 000 km mehr lang, sondern kürzer. Aber er bemerkt ja, daß das Licht in der fraglichen Sekunde auch die Strecke zurückgelegt hat, die der letzte Wagen während dieser Sekunde durchfuhr, und von der natürlich der im Zug fahrende Beobachter nichts gemerkt haben kann. Addiert er nun diese Strecke zu der verkürzten Zuglänge, so kommen auch für ihn gerade wieder die notwendigen 300 000 km der Lichtgeschwindigkeit heraus.

Lorentz' Meinung ist also: Durch Bewegung verkürzen sich alle Gegenstände in der Bewegungsrichtung, aber wegen gleichzeitiger entsprechender Mitverwendung des Maßstabs wird diese Verkürzung nie bemerkt. In der Tat ein Gedanke von überraschender Kühnheit. Jeder korpulente Herr wird schlanker, wenn er sich nur fleißig Bewegung macht! Nur schade, daß er diese Verjüngung nicht nachweisen kann! Es ist wohl kaum nötig, hinzuzufügen, daß die Größe dieser Verkürzung von der Geschwindigkeit der Bewegung abhängt, daß also bei schnelleren Bewegungen eine bedeutendere, bei langsameren eine geringere Zusammenziehung angenommen werden muß. Aus der ja schon oft betonten außerordentlichen Größe der Lichtgeschwindigkeit und der vergleichsweisen Langsamkeit aller andern Bewegungen folgt die geradezu winzige Größe der angenommenen Formenänderung. Selbst Mutter Erde mit ihrer immerhin respektabeln Geschwindigkeit von 30 km in der Sekunde würde ihren 12 000 bis 13 000 km langen Durchmesser nur um etwa 6,5 cm zu verkürzen brauchen, und man kann sich demnach das Schicksal des obenerwähnten korpulenten Herrn, dessen Geschwindigkeit kaum mehr als den 15 000. Teil der Erdgeschwindigkeit ausmacht, wohl klarmachen. (Vgl. S. 44.)

b) Kritik.

Bei aller Bewunderung für die gewaltige Kühnheit und den logischen Scharfsinn der Lorentzschen Auffassung wird man doch bei ihrem Studium ein gewisses Gefühl des Mißbehagens empfinden, das sich bei genauerer Betrachtung noch steigert. Die auf den ersten Anblick etwas fremdartig anmutende Hypothese der Volumenänderung durch bloße Bewegung mag als eine Art Notwehr gegen den obengeschilderten zwingenden Mißstand noch am ehesten gerechtfertigt erscheinen. Viel unbehaglicher ist es schon, daß hier eine recht weittragende physikalische Hypothese aufgestellt und gleichzeitig jede Möglichkeit bestritten wird, sie experimentell zu bestätigen oder zu widerlegen. Denn die gleichzeitige Kontraktion der Maßstäbe nimmt ja die Möglichkeit dazu. Das erinnert, wenn ein vielleicht etwas drastisch anmutender, aber deutlicher Vergleich gestattet ist, an das berühmte einjährige Wunderkind, das zwar fließend lesen, aber leider kein einziges Wort sprechen und auch nicht schreiben konnte, so daß die staunenden Zuschauer keine Möglichkeit hatten, die Lesefertigkeit des Kindes nachzuprüfen. Man darf wohl zweifeln, ob das ihrer Bewunderungsfreudigkeit keinen Eintrag getan hat.

Der schwierigste Punkt der Lorentzschen Auffassung ist doch der folgende: Nehmen wir an, ein Physiker beobachte den vorbeifahrenden Eisenbahnzug, stelle dessen Längsverkürzung fest und freue sich, daß er selbst nicht auch kontrahiert wird. Nun fängt unser Physiker, der vorher nur Physiker war, plötzlich an, Astronomie zu treiben; er lernt das Kopernikanische System kennen und stellt vielleicht fest, daß die Bewegung der Erde (oder besser die Resultierende aus den beiden Bewegungen der Erde) und die des Eisenbahnzugs sich gerade aufheben, der scheinbar bewegte Eisenbahnzug also »in Wirklichkeit« stillstehe, während er selber sich bewege. Nun behält also der Eisenbahnzug seine natürliche Länge, während der Beobachter und mit ihm die gesamte Erde verkürzt wird. Unser Freund fährt in seinen astronomischen Studien fort und erfährt eines Tages von der Bewegung der Sonne und ihres gesamten Planetenanhangs durch den Sternenraum. Nun ist die Sachlage wieder anders und vielleicht wieder gerade umgekehrt. Wenn nun auch hiermit unsere jetzigen astronomischen Kenntnisse aufhören, so hindert uns doch niemand, eine Fortsetzung in immer größeren Systemen zu denken. Unser eigener Zustand wird also abhängig gemacht von dem Entscheid über sehr weit abliegende Fragen, die mit physikalischen Mitteln überhaupt nicht behandelt werden können. Hierauf könnte nun Lorentz erwidern, daß den eben erwähnten Änderungen doch eine sehr reelle physikalische Bedeutung zukomme, nämlich eine Änderung des Bewegungszustandes des betrachteten Systems relativ zum Äther. Dieser Äther gibt bei Lorentz sozusagen das Rückgrat der ganzen Welt ab. Dabei sind nicht nur alle Eigenschaften dieses Äthers unbekannt, auch die Frage nach den etwaigen Grenzen seiner kosmischen Erstreckung scheint völlig unbeantwortbar, ja seine Existenz wird durch keinen einzigen Versuch unmittelbar nachgewiesen. Ja, wenn noch wenigstens der Michelson-Versuch ein positives Resultat gehabt hätte, das dann als eine Art Existenzbeweis des Äthers hätte angesehen werden können!

Je mehr man über diese Dinge nachdenkt, desto fester wird sich folgende Überzeugung festsetzen: Wir nehmen überall nur relative Bewegungen wahr, sie sind das einzige unmittelbar Gegebene, die einzigen Bewegungen, die auch messend durch Experiment verfolgt werden können. Es ziemt aber der empirisch gerichteten Naturwissenschaft, als Elemente ihrer Theorie das wirklich Gegebene anzunehmen.

So war es denn natürlich, daß die Lorentzsche Theorie sehr schnell an Boden verlor, als Albert Einstein durch seine geniale Umdeutung die verloren geglaubte Möglichkeit einer völlig relativistischen Auffassung zurückgewann.

4. Einsteins Relativierung des Raums.

a) Die neue Deutung.

Einsteins Leistung läßt sich vielleicht am besten dahin charakterisieren, daß er die Lorentzsche Theorie mit großer Behutsamkeit auf ein völlig andersartiges Fundament stellte, ihre brauchbaren Teile aber, namentlich manches von ihrer mathematischen Ausgestaltung, im einzelnen durchaus beibehielt. Hingegen wird das, was Lorentz als ein physikalischer Vorgang erschien, auf eigentümliche Art ins Philosophische oder bloß Mathematische umgedeutet, und hierdurch werden die soeben erwähnten Unstimmigkeiten völlig beseitigt. Wir wollen versuchen, wiederum vorsichtig an einzelnen Beispielen tastend, seiner Auffassung, die allerdings dem ersten Verständnis des nicht abstrakt und mathematisch Geschulten erhebliche Schwierigkeiten bietet, näherzukommen.

Kehren wir zum fahrenden Eisenbahnzug zurück! Wie wir nun öfters gehört haben, stellt ihn sich Lorentz verkürzt vor. Einstein aber sagt: Nur insofern diese Verkürzung empirisch feststellbar ist, habe ich Veranlassung, auf sie einzugehen. Also: wie wird sie festgestellt, und vor allem: wer stellt sie fest? Nun, der im Zug mitfahrende Beobachter jedenfalls nicht; denn für ihn ist, wie wir ja ausführlich gesehen haben, die Verkürzung infolge gleichzeitiger Verkürzung des Maßstabs gar nicht wahrnehmbar. Sie existiert also nur für den nicht mitfahrenden, auf dem festen Boden gebliebenen Beobachter. Der fahrende Eisenbahnzug und der ruhende Boden stellen, wie wir uns früher ausdrückten, verschiedene »Systeme« dar, und wir können nun sagen: Die Verkürzung wird nur dann wahrgenommen, wenn eine einem System angehörende Strecke von einem andern System aus gemessen werden soll.

Diese Bemerkung nun bot Einstein die Veranlassung zu seiner merkwürdigen Kritik der Raummessung. Er sagte, wir haben grundsätzlich zwei verschiedene Arten von Streckenmessung zu unterscheiden: solche, bei denen sich der Messende und die zu messende Strecke im selben »System«, d. h. in relativer Ruhe zueinander befinden, und solche, bei denen sie in verschiedenen »Systemen« ruhen, bei denen sich also entweder der Beobachter an der Meßstrecke oder die Meßstrecke am Beobachter vorbeibewegt, was vom relativistischen Standpunkt aus auf das gleiche hinauskommt. Wir wollen uns beide Arten der Messung etwas genauer ansehen. Die geringsten Schwierigkeiten bietet natürlich die erste Art, bei der Beobachter und Meßstrecke sich in gegenseitiger Ruhe befinden. Wird beispielsweise jemandem die Aufgabe gestellt, die Frontbreite eines Hauses zu messen, so steht das Haus ruhig vor ihm, von einer Bewegung ist keine Rede. Er und das Haus befinden sich im gleichen System, nämlich im System der als ruhend betrachteten Erde. Hat nun der Mann einen Metermaßstab, so wird die Ausführung keine Schwierigkeiten machen. Er legt in bekannter Weise den Anfangspunkt des Metermaßstabs auf den Anfangspunkt der Meßstrecke, merkt sich den erhaltenen Endpunkt, legt das Metermaß ein zweites Mal an, so daß jetzt sein Anfangspunkt mit dem Endpunkt der vorigen Messung übereinstimmt, und fährt in dieser Weise fort. Fällt etwa bei der 19. Anlegung des Maßstabs Endpunkt der Meßstrecke und des Maßstabs zusammen, so wird er als Ergebnis seiner Messungsarbeit die Zahl von 19 m angeben. Sollte die Messung nicht aufgehen, so werden in bekannter Weise kleinere Maßstäbe eingeführt, etwa Dezimeter, Zentimeter usw., worauf wir hier nicht weiter einzugehen brauchen. Das Charakteristische dieser Art von Messung ist nun, daß dabei der Zeitbegriff und die Zeitbestimmung nicht die geringste Rolle spielen. Mag unser Mann seine Arbeit schnell oder langsam vornehmen, mag er sich im glücklichen Besitz einer richtig gehenden Taschenuhr befinden, oder mag sie ihm stehen geblieben oder zu Hause liegen geblieben sein, all das ändert weder an seiner Messungsmethode noch an seinem Ergebnis auch nur das allergeringste.

Nun sei im Gegensatz hierzu die Aufgabe gestellt, die Länge eines fahrenden Eisenbahnzuges zu messen. Wie ist dies möglich? Offenbar nicht wie eben durch Anlegen des Maßstabs; denn der Eisenbahnzug würde weiterfahren, während wir das Metermaß anlegen. Auch mit Nebenherlaufen ist es nicht zu machen. Denn physikalisch ist der nebenherlaufende Beobachter von dem auf dem Trittbrett mitfahrenden gar nicht zu unterscheiden. Beide gehören zum System des fahrenden Zuges. Soll dieser wirklich von der festen Erde aus gemessen werden, so muß auf dieser sein Anfangs- und Endpunkt zu einer bestimmten Zeit markiert und alsdann die so erhaltene Strecke nach der vorigen Art bestimmt werden. Es ist also etwa so zu verfahren: Am Eisenbahndamm werden eine Anzahl Leute aufgestellt, die außerordentlich genaue Uhren haben, und ihnen aufgegeben, auf dem Eisenbahndamm Anfangs- und Endpunkt des Zuges zu einer bestimmten Zeit, also etwa um 12 Uhr, durch einen Kreidestrich zu markieren. Die Uhren unserer Gehilfen mögen untereinander auf das genaueste übereinstimmen; wir werden alsbald (S. 32 u. 33) sehen, wie dies zu erreichen ist. Die Leute mögen ferner mit einer beliebigen Präzision arbeiten; so werden wir eine Strecke erhalten, die wir als der Länge des fahrenden Zuges gleich voraussetzen dürfen, und diese, die sich ja nun in unserm »System« befindet, messen wir nun nach der früheren Art. Wir sehen, daß sich diese Art der Messung von der ersten sehr stark unterscheidet; sie ist nämlich keineswegs von der Zeit unabhängig, setzt vielmehr den Gebrauch von Zeitmeßinstrumenten, sog. Uhren, durchaus voraus. Die Messung im gleichen System war vollständig zeitlos, die im fremden System kann es nicht sein, weil der Begriff der Bewegung (und »fremdes« System heißt ja »relativ zum eignen bewegtes« System) den Begriff der Zeit eben voraussetzt, ohne ihn nicht denkbar ist. Die erste Art der Messung ist eine reine Frage der geometrischen Kongruenz, die zweite greift über dies Gebiet wesentlich hinaus.

Wir haben also zwei Arten der Messung. Ist es nun sicher, fragt Einstein, daß bei dieser grundsätzlich verschiedenen Arbeitsmethode sich unter allen Umständen das gleiche Resultat ergibt? Was sagt darüber unsere Erfahrung? Nun, zunächst ganz sicher, daß die zweite Art der Messung so gut wie gar nicht angewandt wird. Wollen wir die Länge eines Eisenbahnzuges feststellen, so lassen wir ihn eben anhalten oder begeben uns auf seine Trittbretter, kurz, suchen auf jede Weise eine relative Bewegung zu ihm auszuschalten, mit ihm in das gleiche System zu kommen. Ebenso wird jeder Fuhrmann, der die Deichsel eines fahrenden Wagens messen will, einfach nebenhergehen und im Weitergehen messen. Uns aber muß es jetzt durchaus darauf ankommen, die Länge einer Strecke von einem andern System aus zu messen oder uns gemessen zu denken, und hierfür kann gar keine andere Methode angegeben werden als unsere obige.

Wir werden also gestehen müssen: Praktische Erfahrungen über die Messungen der zweiten Art liegen kaum vor. Aber auch selbst wenn sie vorlägen oder versucht würden, was wäre von ihnen zu erwarten? Wir wissen, daß alle uns zugänglichen Geschwindigkeiten, ja selbst die der Erdbewegung, im Vergleich mit der uns hier in erster Linie interessierenden Lichtgeschwindigkeit ganz außerordentlich langsam sind. Sie erfolgen samt und sonders geradezu im Schneckentempo! Erfahrungen, die für diese spezielle Art von Bewegungen gemacht sind, brauchten sich nun noch nicht ohne weiteres auf die allgemeine Form der Bewegung übertragen zu lassen. Denn es ließe sich doch wohl – zunächst rein hypothetisch – der Fall denken, daß etwaige Differenzen zwischen beiden Arten der Messung für langsame Bewegungen so geringfügig wären, daß sie selbst unsern feinsten Meßmethoden entgingen, während sie für größere Geschwindigkeiten mehr ins Gewicht fallen könnten.

Die Erfahrung sagt uns also über die Übereinstimmung oder Nichtübereinstimmung beider Arten der Messung nichts aus. Es ist nun ein ganz anerkannter Grundsatz der Technik physikalischer Forschung, wenn über einen Punkt keine bestimmten Erfahrungen vorliegen, auch keine erwartet werden können, es zunächst einmal mit einer mehr oder weniger »plausibeln« Annahme zu versuchen, aus ihr Folgerungen, womöglich auf mathematischem Wege, abzuleiten, und dann zu sehen, wie weit diese Folgerungen mit der Erfahrung übereinstimmen. Von dieser Freiheit macht nun auch Einstein Gebrauch, indem er festsetzt: Wir nehmen an, daß beide Messungsarten nicht miteinander übereinstimmen, daß vielmehr dem Beobachter, der vom ruhenden System aus eine Strecke des bewegten Systems messen will, diese verkürzt erscheine, und zwar gerade im Ausmaß der Lorentzschen Kontraktion. Damit glauben wir unsere ankündigende Bemerkung, daß Einstein die rein physikalische Auffassungsweise Lorentz' ins Mathematische und Philosophische übertragen habe, dabei aber einen großen Teil der alten Auffassung durchaus beibehalten konnte, klargelegt zu haben.

Der sehr große Vorteil der Einsteinschen Auffassung liegt vor allem in der nun wiederhergestellten Relativität. Die von ihm angenommene Verkürzung hängt nicht von Ruhe oder Bewegung an sich ab, sondern nur davon, daß die fragliche Strecke von einem System aus gemessen wird, das relativ gegen ihr System in Bewegung ist. Dabei ist die Beziehung des ersten Systems zum zweiten keine andere als die des zweiten Systems zum ersten. Um dies an unserm Beispiel klarzumachen: Auch wenn der im Zug mitfahrende Beobachter eine Strecke des festen Bodens messen will, kann er dies nur nach der zweiten »Methode« tun, denn der Boden ist relativ gegen ihn bewegt, so gut wie er gegen den Boden. Die Beziehungen sind durchaus wechselseitig, was einen Hauptgrundstein der ganzen Einsteinschen Auffassungsweit ausmacht. Bei Lorentz war dies ausgeschlossen, denn eine physikalische Verkürzung ist eben absolut, sie kann nicht abhängig gedacht werden vom Beobachter, der sie wahrnimmt. In der Praxis kann natürlich auch Lorentz nicht umhin, sich auf relativistischen Boden zu stellen. Seine Theorie aber ist absolutistisch. Einstein hat diese Diskrepanz zwischen Theorie und Praxis beseitigt.

Zweifellos wird dieser Einsteinschen Raumauffassung der Vorwurf gemacht werden, daß sie allzu abstrakt und unanschaulich sei, und daß außerdem ihre Lehre von der Dissonanz der beiden Messungsmethoden dem gesunden Gefühl, das die Identität beider Messungsresultate schlechthin gebieterisch fordere, allzusehr widerstreite. Nun möchte ich mich auf eine Erörterung der Rolle, die das gesunde Gefühl in der Wissenschaft zu spielen hat, nicht einlassen, betrachte es überhaupt lediglich als meine Aufgabe, dem Leser die Relativitätstheorie so nahe wie möglich zu bringen und sie seinem Verständnis zu erschließen. Nicht aber möchte ich alle Einwände oder Bedenken, die sich in diesen anerkanntermaßen höchst schwierigen Fragen erheben lassen, als schlechthin unberechtigt oder gar töricht hinstellen. Immerhin sei folgendes bemerkt: Die Bedeutung der Anschaulichkeit in der Wissenschaft, so groß sie ist, darf nicht überschätzt werden. Zweifellos ist es die Anschauung, die in den allermeisten Fällen dem Forscher den Weg in noch unerschlossene Gebiete weist; sie beflügelt seine Phantasie, ohne die auch er nicht schaffen kann. Andrerseits ist es wieder die Anschauung, die dem Lernenden den Weg für neue Gedankengänge bahnen muß. Aber hierin liegt ihre Bedeutung auch beschlossen! Das letzte Kriterium für den Wert und die Richtigkeit einer Lehre kann ihre Anschaulichkeit niemals abgeben. Im Kampf zwischen leichtverständlicher Anschaulichkeit einerseits und mathematisch geschärfter, abstrakter Logik andrerseits wird, wie uns die Geschichte der Wissenschaft vieler Jahrhunderte gezeigt hat, die letztere immer Siegerin bleiben. Wünscht man durchaus eine Veranschaulichung, so wird sie vielleicht am besten durch folgendes, öfters von Petzoldt gebrauchte Bild geboten: Auch wenn wir einen Gegenstand betrachten, ist ja das Bild, das wir von ihm empfangen, nicht nur vom betrachteten Objekt, sondern auch von unserm eignen Standpunkt abhängig. Wo immer wir diesen wählen, perspektivische Verkürzung können wir niemals ausschalten. Aber bei aller Verschiedenartigkeit der erhaltenen Bilder zweifeln wir doch nicht daran, daß sie vom selben Gegenstand herrühren. Nun waren wir bisher überzeugt, daß zwar nicht das menschliche Auge, wohl aber physikalische Meßmethoden einen Vorgang ganz objektiv aufzunehmen vermögen. Das verneint die Einsteinsche Auffassung, indem sie behauptet, daß der Bewegungszustand des Beobachters in alle, auch die scheinbar objektivsten physikalischen Messungen mit eingehe. Sie liefern also alle nur Bilder des Vorgangs, sozusagen mit einer gewissen Perspektive behaftet. Steht nun hinter diesen verschiedenen Bildern überhaupt noch ein uns freilich ganz unzugänglicher objektiver Vorgang, oder sind diese selbst die schlechthin letzte greifbare Realität? Mit aller Energie vertritt J. Petzoldt den letzteren Standpunkt, doch müssen wir uns hier mit der bloßen Aufwerfung dieser Frage begnügen.

Eine »Veranschaulichung« der Relativitätstheorie sind diese Bemerkungen nicht und können sie nicht sein; denn diese ist eben unanschaulich und deswegen schwierig. Aber diese Schwierigkeiten sind keineswegs sozusagen mutwillig von der Theorie heraufbeschworen. Sie liegen vielmehr in den Erfahrungstatsachen begründet. Um die scheinbare Unvereinbarkeit der beiden grundlegenden Versuche zu beheben, bedurfte es eines kühnen Entschlusses; Einstein hat ihn gefaßt, und allem Anschein nach ist er ihm gelungen.

b) Licht, Äther und Anschaulichkeit.

Unsere letzten Bemerkungen über Anschaulichkeit in der Naturwissenschaft erhalten eine merkwürdige Illustration durch die Geschichte unserer Vorstellungen von der Natur des Lichts. Die alte Newtonsche Emissionstheorie, die das Licht aus fortgeschleuderten Massenteilchen bestehen ließ, war ohne Zweifel recht anschaulich. So hielt sich denn diese Lehre auch noch weiter, selbst nachdem sie für unsere Begriffe durch die Interferenzerscheinungen, von denen übrigens eine Newton selbst bekannt war, unzweifelhaft widerlegt war. Auch die Huygenssche Wellenlehre ist noch anschaulich. Wenn freilich auch die Vorstellung von Wellen, die so klein sind, daß ihrer 2000 auf einen Millimeter gehen, und die doch einander so schnell folgen, daß sie die Strecke von Köln nach Königsberg 300 mal in einer Sekunde durchqueren, äußerst schwierig ist, so liegt darin doch noch kein grundsätzlicher und kein gewollter Verzicht auf die Anschaulichkeit. Im Gegenteil! Darin, daß die Theorie der elastischen Schwingungen im Äther trotz handgreiflicher Schwierigkeiten so lange aufrechterhalten blieb, zeigt sich das deutliche Bestreben, alle Vorgänge unter mechanisch geläufigen Bildern zu begreifen, die Bewegungsvorgänge als den Kern alles Naturgeschehens zu betrachten und die Anschaulichkeit um jeden Preis zu retten. Keine inneren Schwierigkeiten waren es, an denen schließlich diese elastische Theorie scheiterte, sondern die positive Aussicht auf neue Triumphe der Wissenschaft, die sich vor allem an die Namen Faraday, Maxwell und Hertz knüpfte. Die Anschaulichkeit aber erlitt durch die neue elektromagnetische Lichttheorie einen argen Stoß. Die mit rasender Geschwindigkeit hin und her schwingenden Ätherteilchen waren zur Not noch vorstellbar, aber was sollte man anfangen mit einem ebenso schnell sich durch den Weltenraum fortpflanzenden Kraftfeld mit seinem stets wechselnden Doppelspiel von senkrecht aufeinander stehenden elektrischen und magnetischen Kräften! Und doch waren diese elektrischen und magnetischen Kräfte, die auf ihrem ganzen weiten Wege kein andere Möglichkeit zu wirken hatten, als die, neue Kräfte gleicher Art hervorzurufen, das einzige, was man sich unter der Lichtfortpflanzung zu denken hatte. Mit der anschaulichen Bewegung materieller Teilchen hatte diese ganze Vorstellung nichts mehr zu tun, in ihr lag also schon der Verzicht auf eine eigentlich mechanische, d. h. allein auf Bewegung gegründete Weltanschauung. Aber große Teile der Physik, die Mechanik, die Akustik, die Wärmelehre, auch wohl die ganze Chemie blieben von diesem Wechsel der Anschauung unberührt, hier wenigstens war eine mechanische Anschauung noch gestattet. Freilich wuchs trotz des letzten großen Triumphs, den die mechanische Anschauung in der glänzenden, höchst anschaulichen kinetischen Gastheorie Boltzmanns erringen konnte, die Bedeutung und der Umfang der mechanisch nicht erklärbaren Teile der Physik insbesondere durch die Entdeckungen von Röntgen, Bequerel, Frau Curie, Rutherford, Laue und Planck immer mehr an.

Wir nehmen die schon oben besprochene Deutung der Versuche von Fizeau und Michelson wieder auf. Wie schon gesagt, läßt sie sich dahin präzisieren, daß das Licht, vom ruhenden System aus beobachtet, im ruhenden schwingt, vom bewegten aus beobachtet, im bewegten. Da wir einen grundsätzlichen Unterschied von bewegtem und ruhendem System nicht mehr anerkennen werden, so können wir auch sagen: Das Licht gehört dem System des jeweiligen Beobachters an, es ist, um einen glücklichen Ausdruck Blochs zu wiederholen, »Kosmopolit«; es sagt freilich nicht: ubi bene, ibi patria, sondern: wo ich gesehen und beobachtet werde, da ist mein Vaterland.

Suchen wir uns dies noch weiter zu »veranschaulichen«: Wir haben bisher nur von linienförmiger Fortpflanzung des Lichtes gesprochen; in Wirklichkeit bewegt es sich ja bekanntlich nach allen Richtungen des Raumes, also kugelförmig nach allen Seiten. Nehmen wir nun an, im freien Weltenraum werde an einem bestimmten Punkt ein Lichtblitz losgelassen, und gleichzeitig werde dieser Punkt von einer beliebig großen Schar von Beobachtern durchflogen, die von den verschiedensten Seiten, jeder mit einer andern Geschwindigkeit, jedoch alle geradlinig-gleichförmig, herangeeilt kommen. Was werden alle diese Beobachter sehen? Machen wir uns ihre Beobachtungen an dem Bild eines ins Wasser geworfenen Steines klar, der ein System konzentrischer Ringe zieht. Die Ringe wachsen und wachsen nach außen, aber wie groß sie auch werden, sie lassen jederzeit noch deutlich den Mittelpunkt erkennen, von dem sie ausgegangen sind, und um den sie sich konzentrisch herumlagern. Auch macht es unserer Anschauung keine erheblichen Schwierigkeiten, uns das Ringsystem etwa in einem vollkommen sanft und stetig fließenden Fluß vorzustellen, der die Kreise mitsamt ihrem Mittelpunkt stromabwärts trägt. Dieser ganze bekannte Vorgang der Wellenausbreitung findet eben statt in dem als relativ ruhend angenommenen System des Wassers. Und doch können wir uns, und zwar ohne Schwierigkeit, vorstellen, daß dieses ganze Wassersystem bewegt sei, relativ etwa zu dem nun als ruhend angenommenen Ufer.

Das aber überschreitet unsere Anschauungskraft, uns vorzustellen, daß wir zu dem nämlichen fortschreitenden Wellensystem verschiedene Mittelpunkte anzunehmen haben, die von demselben Punkt aus, zwar erheblich langsamer als die Wellenbewegung, aber auch noch mit merklicher Geschwindigkeit, auseinander streben und dabei doch noch in jedem beliebigen Zeitmoment Mittelpunkte der fortschreitenden Wellenbewegung bleiben. Eben zu dieser Annahme sind wir aber durch die Tatsachen der Lichtausbreitung gezwungen, und zwar sogar noch unabhängig von jeder Theorie! Denn die Tatsachen zeigten uns doch, daß jeder Beobachter, gleichviel wie er sich selber auch bewegen möge, die gleiche Lichtgeschwindigkeit um sich herum wahrnimmt, im Raume also ein konzentrisches Kugelsystem mit sich selbst im Mittelpunkt annehmen muß. Als fließend können wir uns das Wasser vorstellen; aber es übersteigt die Kräfte unserer Phantasie, anzunehmen, daß es gleichzeitig nach mehreren, ja beliebig vielen Richtungen auseinander fließe, so daß der im Augenblick der Wellenentstehung einheitliche Mittelpunkt sich nun zerteile, wobei aber jeder einzelne nun entstehende Punkt nach wie vor Mittelpunkt der gemeinsamen Wellenbewegung bleibt.

Kehren wir zu der räumlichen Anschauung und den Lichtkugeln zurück! Wie ist der Streit um die Kugeln zu schlichten? Lorentz sagt: Nur ein System konzentrisch wachsender Kugeln ist das echte, nämlich das im absolut ruhenden Äther, und nur wenn ein Beobachter im Äther ruht, so fällt die von ihm wahrgenommene Kugel mit der absolut richtigen zusammen. Daß auch die übrigen sich jederzeit im Mittelpunkt der von ihnen wahrgenommenen konzentrisch fortschreitenden Kugeln zu befinden glauben, das ist eine Täuschung, die durch die Veränderung der Maßstäbe dem Auge der Beobachter entzogen bleibt. – Einsteins Urteil erinnert etwas an Nathan den Weisen mit seinen drei Ringen! Er sagt: Jede Kugel ist die echte, freilich nicht die absolut echte, sondern nur relativ, d. h. für ihren Beobachter. Sieht aber ein Beobachter aus seinem System in ein fremdes, so erscheint ihm die dortige Kugel verzerrt; aber nicht, weil sie an sich verzerrt wäre, sondern nur, weil er bei dem Überschreiten der Grenzpfähle seines Systems die Maßstäbe, die sich innerhalb seines Systems durchaus bewährt haben, unberechtigterweise weiter anwendet. Nicht als ob das fremde System von seinem eigenen an sich verschieden wäre, im Gegenteil, alle Systeme gleichen sich wie ein Ei dem andern; nur in dem Messen aus einem System heraus in ein anderes hinein liegt eine Kritiklosigkeit, die sich gerächt hat.

Und wo ist unser Äther geblieben? Er hat seine Existenzberechtigung eingebüßt! Er wäre, um obiges Bild wieder aufzunehmen, dem Wasser zu vergleichen, das gleichzeitig nach mehreren oder eigentlich sogar beliebig vielen Richtungen auseinander fließt; oder auch dem Floß auf S. 16, das mit dem ruhenden Beobachter stillsteht und zur selben Zeit mit dem bewegten stromab treibt. Physikalisch, chemisch und astronomisch war er von jeher ein mehr als dürftiger Geselle, der eigentlich nur über Wasser gehalten wurde, um die Lichtbewegung zu erklären. Aber gerade deren Verständnis wird nach Einstein durch den Äther eher erschwert als erleichtert. Denn worauf es uns beim Licht in allererster Linie ankommt, und was der Erklärung demnach vor allem bedarf, das ist die Konstanz seiner Fortpflanzungsgeschwindigkeit für jeden Beobachter, die nur durch einen Äther, der relativ zu diesem ruht, verständlich ist. Der Äther müßte also relativ zu allen Beobachtern ruhen, oder was dasselbe bedeutet, sich in allen möglichen Bewegungszuständen zugleich befinden. Ein Stoff aber, der nicht nur aller physikalischen und chemischen Eigenschaften, sondern sogar eines bestimmten Bewegungs- und Ruhezustandes ermangelt, gleicht denn doch allzusehr dem berühmten Messer ohne Klinge, dem der Stiel fehlt.

Damit aber ist auch zugleich der letzte Rest von Anschaulichkeit geopfert. Ein Kraftfeld, das sich mit ungeheurer Schnelligkeit und in noch schnellerem, absolut regelmäßigen, periodischen Wechsel durch den leeren Raum verbreitet, ohne daß das mindeste materielle Substrat, an dem diese Ausbreitung geschehen könnte, nachweisbar oder auch nur vorstellbar wäre, und das sich dabei noch nach dem Beobachter, der es wahrnimmt, zu richten scheint, spricht jedem Veranschaulichungsbestreben Hohn.

Veranschaulichung eines Vorgangs ist aber nichts anderes als seine Verständlichmachung durch ein wirkliches oder gedachtes mechanisches Modell, denn das einzige, was restlos anschaulich ist, sind die Bewegungsvorgänge. Die Ansicht, daß sich das gesamte Naturgeschehen auf Bewegungsvorgänge zurückführen lasse, nennt man bekanntlich mechanische Weltanschauung. Sie ist nach dem Vorigen nicht aufrechtzuerhalten. Es wird sich auch zeigen, daß die alten mechanischen Prinzipien und die neuen elektromagnetischen nicht etwa gleichberechtigt nebeneinander bestehen bleiben, sondern daß wohl die ersteren eine Unterordnung unter die letzteren vertragen, das Umgekehrte jedoch nicht möglich ist. So hat die abstrakt-mathematische Weltanschauung über die anschaulich-mechanische auf der ganzen Linie gesiegt. Ob es nun im Prinzip möglich ist, alle »Dinge zwischen Himmel und Erde« zwar nicht auf Bewegungsvorgänge, aber doch auf quantitativ meßbare und also der mathematischen Behandlungsweise zugängliche Größen zurückzuführen, darüber soll mit diesen Worten weder in positiver noch in negativer Richtung etwas gesagt oder angedeutet sein.

Schließlich sei noch für Leser, denen die eben gebrauchten Bilder der konzentrischen – und doch wieder exzentrischen – Lichtkugeln etwa zu abstrakt und schwierig vorgekommen sein mögen, gesagt, daß ihnen zuliebe, um die Schwierigkeiten für den Anfang nicht zu häufen, schon eine merkliche Vergröberung der mathematisch korrekten Bilder stattgefunden hat. Eine wirklich strenge Auffassung bedarf außer einer Relativierung des Raumbegriffs auch einer Relativierung des Zeitbegriffs, der wir uns nunmehr zuwenden.

5. Die Relativierung der Zeit.

Die Relativierung der Zeit scheint gemeinhin dem Verständnis noch weit größere Schwierigkeiten zu bereiten als die des Raumes. Die Zeit, so wird etwa argumentiert, sei doch eben ein stetiges Fließen, das nur dem inneren Sinn, diesem aber auch vollkommen deutlich zugänglich sei und daher nicht abhängig gedacht werden könne von irgendwelchen äußeren Geschehnissen. Die Zeit sei daher notwendig absolut zu verstehen. Um dieser Argumentation die Spitze abzubrechen, wäre es allerdings vielleicht richtiger, statt von einer »Relativierung der Zeit« lieber von einer »Relativierung der Zeitmessung« zu sprechen und es alsdann getrost dem Leser zu überlassen, wieviel er nach der Relativierung der Zeitmessung von der absoluten Zeit noch übrig behalten will. Wir wenden uns nun zu den

a) Prinzipien der Zeitmessung und Fragestellung.

Wir nehmen an, wir seien im Besitze einer tadellos gehenden Uhr, die in bekannter Weise durch die scheinbare tägliche Umdrehung des Himmelsgewölbes auf astronomischem Wege kontrolliert werde und eine beliebig genaue Zeitablesung gestatte. Ist nun hierdurch die Frage der Zeitmessung gelöst? Solange wir dauernd mit der Uhr am selben Ort bleiben, gewiß! Wir wünschen aber die Zeit gleichmäßig für ein größeres Gebiet festzulegen, so also, daß sich an beliebig vielen Punkten des Gebietes Uhren befinden, die zu gleicher Zeit auch haarscharf die gleiche Zeit anzeigen. Wie kann dies geschehen? Man könnte auf folgenden Gedanken kommen: Man lasse sich eine genügende Zahl guter Uhren herstellen, vergleiche sie eine Zeitlang mit der als Normaluhr anerkannten, reguliere sie, solange dies nötig ist, und bringe sie schließlich an den verlangten Ort. Ist dies für genügend zahlreiche Orte durchgeführt, so ist die Zeit für unser Gebiet definiert. Hierauf ist zu erwidern: Rein theoretisch ist der Vorgang des Uhrentransportes recht schwer faßbar. Es ist nicht klar, wie dies mathematisch ausgedrückt werden kann. Ferner: Wer gibt die Gewähr, daß die Uhr nicht infolge des Transportes anders geht als vorher? Pendeluhren z. B. hängen in ihrem Gang von dem Ort ab, an dem sie sich befinden, alle Uhren richten sich mehr oder weniger nach der Temperatur; außerdem, auch von allen Nebenumständen abgesehen, könnte nicht auch eine Uhr, die tadellos ging, solange sie sich bei der Normaluhr befand, ihre Unzuverlässigkeit erst bekunden, sobald sie allein ist? Dies leugnen, hieße einfach, die Geschicklichkeit des Uhrmachers absolut zu setzen, und dies wird kaum unsere Absicht sein. Wir werden vielmehr zugeben müssen: Soll sich die Zeitmessung auf ein größeres Gebiet erstrecken, so ist dauernde gegenseitige Kontrolle der Uhren, deren Wiederholung sogar beliebig oft möglich sein muß, ganz unumgänglich. So wird ja auch in der Praxis verfahren. Alle Uhren, für die eine einheitliche Zeit, also beispielsweise die mitteleuropäische Zeit, gelten soll, sind durch ein bestimmtes Signalsystem unter sich verbunden, das die sicherste Gewähr dafür bietet, daß die von einer Uhr angegebene Zeit auch von der andern geliefert wird. Wesentliche Schwierigkeiten treten nicht auf, solange das Gebiet so klein ist, daß für die fragliche Nachrichtvermittelung an sich keine merkliche Zeit gebraucht wird. Bei der sehr großen Geschwindigkeit, mit der sich optische, elektromagnetische, elektrische Zeichen fortpflanzen lassen, könnte ja ein solches Gebiet nach gewöhnlichen, z. B. geographischen Begriffen immerhin noch recht groß sein, es könnte wohl ziemlich unbedenklich die ganze Erde umfassen.

Nun nehmen wir aber an, unser mit Uhren zu versehendes Gebiet sei so groß, daß die Zeit, die zur Nachrichtenvermittelung gebraucht wird und die ja unter allen Umständen eine endliche ist, nicht mehr vernachlässigt werden darf. Es ist dann in folgender Weise zu verfahren: Zu einer bestimmten Zeit, sagen wir um 12 Uhr, gibt ein Beobachter A ein Zeichen. Kommt dies Zeichen bei einem zweiten Beobachter B an, so darf er natürlich nicht etwa seine Uhr auch auf 12 Uhr stellen, sondern er muß die Zeit, die zur Nachrichtenübermittelung gebraucht wird, noch addieren und erhält erst dann die Zeit, auf die er seine Uhr einstellen muß. Wegen der großen Wichtigkeit dieser Korrektion wollen wir ihre Notwendigkeit noch besonders beweisen. Nehmen wir an, die drei Punkte A, B und C liegen in einem gleichseitigen Dreieck. Es gebe nun A sein Zeichen, und B und C stellen nach Empfang des Zeichens ihre Uhr ohne Korrektion ein. Nun werden die Uhren von B und C ganz gleich gehen, beide hingegen gehen gegen die Uhr von A nach, und zwar um die Zeit, die zur Nachrichtenübermittelung gebraucht wurde. Soll nun aber das Zeichen nicht von A, sondern von B oder C aus gegeben werden, so springt der Widerspruch natürlich sofort in die Augen. Eine für unser gesamtes System gültige Zeitdefinition wäre offenbar auf diese Weise nicht zu erhalten.

Die Zeit, die zur Signalgebung gebraucht wird, muß also berücksichtigt werden. Natürlich arbeiten wir mit optischen Signalen, denn diese sind ja schlechtweg die einzigen, die über die Erde hinausreichen, und außerdem würde auch die Verwendung anderer Zeichen nicht zu einer Klärung der uns interessierenden Fragen führen. Es gebe also A seinen Lichtblitz ab; ist er bei B angekommen, so stellt B seine Uhr nicht ohne weiteres danach ein, sondern bringt die notwendige Korrektion an. Ausrechnen kann er diese freilich nur dann, wenn ihm die Entfernung AB und die Lichtgeschwindigkeit bekannt ist. Vorsichtshalber kann übrigens auch folgendermaßen verfahren werden: A gibt sein Signal ab, und B telegraphiert sofort nach Erhalt zurück. A halbiert die Zeit, die zwischen Absendung und Empfang liegt, und lernt auf diese Weise die notwendige »Korrektion« kennen. Wird in umgekehrter Weise verfahren, so kann auch B sie kennen lernen und sinngemäß verwenden. Nun können beide Beobachter ihre Uhren aufeinander einstellen. Uhren, die in dieser Weise aufeinander eingestellt und in dauernder Kontrolle, gehalten werden, nennt man gleichgehende oder synchrone Uhren.

Das Vorangegangene wird nun freilich nur in dem Falle zu keinen besonderen Schwierigkeiten führen, wenn A und B relativ gegeneinander ruhen, oder wenn sie, wie wir uns früher ausdrückten, zum gleichen System gehören. Wir wollen also diese Voraussetzung machen und uns zugleich noch beliebig viele weitere Uhren an allen möglichen Punkten unseres Systems angebracht denken. Nun läßt sich ohne Schwierigkeiten zeigen, daß zwei Uhren, die einer dritten synchron gehen, auch untereinander synchron gehen. Ich brauche also nur eine für das System gültige Normaluhr aufzustellen und danach alle andern Uhren synchron einzustellen, und die Frage der Zeitbestimmung wäre für unser System in völlig befriedigender Weise gelöst. (Hiermit ist auch die auf S. 23 gebliebene Lücke ausgefüllt.)

Nun jedoch denken wir uns mehrere, sagen wir zwei Systeme gleichzeitig, die sich geradlinig-gleichförmig gegeneinander bewegen. Die Systeme mögen, wie auch bisher schon, rein mathematisch gedacht sein, so daß sie sich ohne Schwierigkeit gegeneinander und ineinander schieben lassen. Sie können linienförmig gedacht sein, so daß wir zwei Linien haben, die gegeneinander bewegt werden, jedoch so, daß sie stets auf dieselbe Linie zu liegen kommen. Oder wir können uns auch flächenhaft ausgebreitete Systeme denken, etwa symbolisiert durch zwei Blätter Papier, die aufeinander gelegt sich geradlinig-gleichförmig gegeneinander bewegen. Oder schließlich Räume, die gegeneinander fliegen. Jeder Punkt kann nun gleichzeitig beiden Systemen angehören, oder, was dasselbe ist, jeder Punkt eines Systems deckt sich mit einem bestimmten Punkt des andern Systems, allerdings nur momentan. Nun denken wir uns überall Uhren angebracht. Unter allen Umständen, daran wolle man unbedingt festhalten, verlangen wir, daß alle Uhren desselben Systems untereinander synchron gehen. Nun mögen ferner zwei Uhren der beiden verschiedenen Systeme, die sich aber zu einem bestimmten Zeitmoment gerade an demselben Raumpunkt befinden, in diesem Augenblick dieselbe Zeit angeben. Wir fragen nun: Folgt hieraus, daß auch im allgemeinen zwei Uhren verschiedener Systeme in dem Augenblick, wo sie sich an identischen Punkten befinden, also sozusagen aneinander vorbeifliegen, dieselbe Zeit angeben?

b) Ein Beispiel.

Wir denken uns zwei ebene Systeme, also etwa ein Blatt Papier und ein unmittelbar dahinter befindliches. Das vordere denken wir uns ruhend, während das hintere (in der Figur gestrichelte) nach rechts bewegt wird. In dem vorderen Blatt befinde sich ein Beobachter B, in dem hinteren ein solcher B' (Fig. a). Im Punkt A werde nun ein Lichtblitz abgegeben, dieser Punkt A ist also als beiden Systemen angehörig zu betrachten. Der Lichtblitz verbreite sich und komme in dem Punkte B gerade im Augenblick der Fig. b an, wo der bewegte Beobachter B' am festen B vorübersaust. Der bewegte Beobachter B' empfängt also den Blitz, der zu der Zeit abgegeben, wurde, als er sich in der Lage der Fig. a befand, erst in der Lage der Fig. b; der Ausgangspunkt des Signals, der als solcher beiden Systemen angehört, ist als Punkt des festen Systems in A geblieben; als Punkt des bewegten Systems und für den bewegten Beobachter hat er sich nach A' verschoben. Wir erinnern uns des Beispiels S. 17, wo der fahrende Beobachter das Signal als auf dem Zug abgegeben, der ruhende Beobachter dasselbe Signal als auf dem festen Boden abgegeben annehmen wird. Der ruhende Beobachter wird also die Lichtquelle in A, der bewegte Beobachter wird sie in A' suchen. Man muß sich nachdrücklich klarmachen, daß beide damit in völlig gleichem Rechte sind. Es ist durchaus nur ein Mangel unserer Ausdrucksweise und unserer Zeichnungen, daß wir den einen Beobachter als den »ruhenden« bezeichnen und dadurch augenscheinlich bevorzugen. Die Wirklichkeit zeigt uns keine »Ruhe« und »Bewegung«, sondern nur »relative Bewegung«. Wollte man etwa sagen: Wir halten einfach alle Bewegungen an, lassen sie stillstehen und untersuchen dann, welches die richtige Richtung von B aus ist, die nach A oder die nach A', so ist zu erwidern, daß doch eben dieses »Anhalten« oder »Stillstehenlassen« der Bewegungen einen absoluten Raum voraussetzen würde. Außerdem müßte doch das Anhalten sinngemäß nicht in dem Moment geschehen, wo der Lichtblitz ankommt, sondern in dem, wo er ausgesandt wurde. Denn was die Lichtquelle in der Zwischenzeit angefangen hat, ist ja ganz gleichgültig; sie kann ja auch, wenn es sich wirklich nur um einen Lichtblitz handelte, längst erloschen sein. Aber für den Augenblick der Lichtaussendung ist das Anhalten wieder überflüssig, denn für diesen besteht ja gar kein Streit, da sich zu jener Zeit die jetzt getrennten Punkte A und A' eben deckten. Und nach wie vor wird B den Punkt A, B' den Punkt A' als den echten Nachfolger des ehemals vereinigten Punktes erklären.

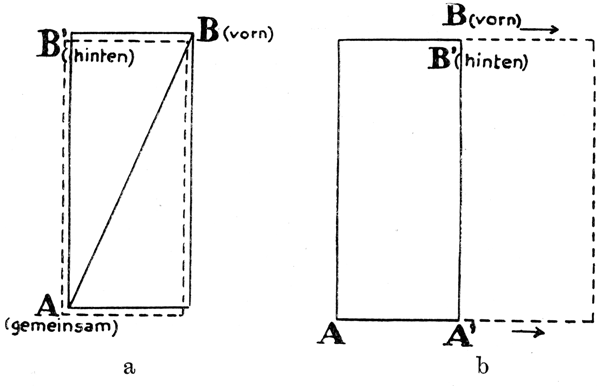
Beide Beobachter nehmen also den Lichtblitz gleichzeitig in B wahr. Seinen Ursprung aber suchen sie mit gleichem Recht der eine in A, der andere in A'. Nun müssen sie aber beide, wie oben aus diesem Grunde ausführlich besprochen, an ihrer Beobachtung eine »Korrektion« anbringen, nämlich zu der signalisierten Zeit noch die Zeit für den Lichtweg addieren. Und diese Zeit fällt für die beiden Beobachter verschieden aus; denn der eine nimmt ja als Lichtweg AB, der andere A'B an. Die Zeit aber, die das Licht für AB brauchen würde, ist ganz augenscheinlich größer als zu A'B. Der als ruhend angenommene Beobachter addiert also zu der gemeinsam gemachten Beobachtung eine größere Korrektionszeit, seine Uhr geht also vor, die des bewegten Beobachters geht nach. Es sei nun jedes der beiden Systeme im Sinne des vorigen Abschnittes mit synchron gehenden Uhren ausgestattet. Die beiden Uhren A und A' zeigten in dem Augenblick, wo sie in A aneinander vorbeiflogen, die gleiche Zeit; unsere Betrachtung zeigt, daß nun doch eine gemeinsame Zeit für beide Systeme in der Art, daß am gleichen Ort befindliche oder aneinander vorbeifliegende Uhren zu gleicher Zeit auch die gleiche Zeit angeben könnten, nicht möglich ist.

Es dürfte nicht ohne Interesse sein, dieses Beispiel rechnerisch durchzuführen. Nehmen wir als Beispiel die Erdgeschwindigkeit an. Unsere Erde möge sich also mit der Geschwindigkeit, die sie bei ihrer Bahn um die Sonne entwickelt, in stets geradliniger Richtung weiterbewegen. Wir selbst befinden uns als bewegter Beobachter B' auf ihr und bewegen uns nach B, allwo wir einen fest gebliebenen Beobachter antreffen. Wir beide beobachten nun den von A ausgegangenen Lichtblitz, jedoch in etwas verschiedener Richtung. Es ist klar, daß dieser Richtungsunterschied, also der Winkel ABA', sehr viel kleiner sein wird als in der Figur. Denn der Weg der Erde von B' nach B (Fig. a) und der ihm gleiche gedachte Unterschied der beiden Punkte A und A' ist ja sehr klein im Verhältnis zu dem Weg AB, den das Licht in gleicher Zeit zurückgelegt hat.

Wir fragen nun: Wie lange muß die Erde ihren geradlinigen Weg fortsetzen, damit der auf diese Weise entstehende Zeitunterschied der Lichtwege AB und A'B gerade eine Sekunde beträgt? Die Antwort lautet in runder Zahl: 6 bis 7 Jahre. Die Strecken B'B und AA' betragen also 6 »Erdjahre«, das 6fache des Kreisumfangs der Erdbahn. Zur Strecke AB hingegen würde das Licht 6 Jahre gebrauchen und die Strecke A'B ist nur um eine »Lichtsekunde«, d. h. um 300 000 km kürzer. Der Winkel ABA' beträgt etwa ⅓ Minute, ziemlich genau den hundertsten Teil des scheinbaren Sonnen- oder Vollmonddurchmessers. Wir kommen auf ihn noch zurück.

Die nächsten Fixsterne sind von uns einige Lichtjahre entfernt. Einige würden sich also wohl auftreiben lassen, die uns kaum weiter stehen als die sechs Lichtjahre der Strecke AB. Vom Standpunkte der gesamten unserm Fernrohr zugänglichen Fixsternwelt aus würde es immerhin noch sozusagen die nähere Nachbarschaft sein. Nehmen wir also an, es werde in A ein Lichtzeichen gegeben, das für die gesamte Nachbarschaft den Beginn einer neuen Zeitrechnung darstellen solle, so würden zwar beide Beobachter genau das gleiche Datum schreiben, auch Stunden- und Minutenzeiger ihrer Uhren stimmten noch überein, der Sekundenzeiger aber würde, obwohl sich beide am gleichen Orte befinden und beide gleich gewissenhaft beobachtet haben, doch eine Differenz von einer Sekunde aufweisen, um die unsere Uhr als die des bewegten Beobachters nachgehen würde.

Dieses Beispiel zeigt die außerordentliche Geringfügigkeit der Änderungen, die durch die Betrachtungsweise der Relativitätstheorie nötig werden Es ist notwendig, auf die außerordentliche Kleinheit der durch unsere Theorie bedingten Änderungen in der Zeitrechnung hinzuweisen. Wenn also deswegen, weil die Uhr des bewegten Beobachters nachgeht, gelegentlich darauf hingewiesen wird, daß die Uhr beim Reisen ständig nachgehe, und daß deswegen das Reisen verjünge, so ist das natürlich eine drastische Ausdrucksweise, ebenso wie unser auf Seite 19 gebrauchtes Beispiel von dem korpulenten Herrn, der durch Bewegung schlank wird. Es scheint aber Leute zu geben, die derartige harmlose Scherze für bare Münze nehmen. Noch auf einen andern Fehler muß ich hier hinweisen: Bewegen sich zwei Beobachter aneinander vorbei, so kann vom Standpunkt der Relativitätstheorie aus jeder sich für ruhend und den andern für bewegt halten. Treffen sich aber die beiden Beobachter nachher wieder, so muß doch einer von ihnen einmal umgekehrt sein, was mit geradlinig-gleichförmigen Bewegungen nicht zu machen ist. Mindestens einer also kann sich jetzt nicht mehr für in Ruhe geblieben halten. Dieser Sachverhalt ist schon so oft (z. B. von Einstein in seinem Dialog, von Bloch Seite 68, vgl. Literaturverzeichnis) klargestellt, daß ich ursprünglich dachte, ein Eingehen auf ihn erübrige sich. Nun hat aber in einer am 24. August 1920 in Berlin in der Philharmonie stattgefundenen, von weit über 1000 Menschen besuchten Versammlung der Hauptvortragende beide hier besprochenen Fehler miteinander verquickt. Er behauptete, vom Standpunkt der Relativitätstheorie könne jeder der Beobachter dem andern zurufen: Ich bin in Ruhe geblieben, und du hast dich bewegt; also bin ich gealtert, und du bist jung geblieben; oder in konsequenter Fortführung: Ich bin gestorben, und du lebst noch!!!. Denn im gewöhnlichen Leben und auch in der Wissenschaft arbeiten wir ja mit Geschwindigkeiten, die sehr viel kleiner sind als die Erdgeschwindigkeit, mit Zeiten, die kleiner sind als 6 Jahre und auch mit viel kleineren Strecken. Daß wir also im gewöhnlichen Leben und sogar in der Vor-Michelsonschen Physik mit absoluten Vorstellungen ohne Widerspruch mit der Erfahrung ganz gut ausgekommen sind, darf keineswegs als eine Widerlegung des Relativitätsprinzips angesehen werden. Die alten mechanischen, vor allem auf Galilei und Newton beruhenden Grundsätze ordnen sich eben in ihrem kleineren räumlichen und zeitlichen Bereich dem Relativitätsprinzip sehr gut ein und können sozusagen für den Hausgebrauch auch weiterhin unbedenklich in Geltung bleiben. Für größere Bereiche aber sind sie dem allgemeineren elektromagnetischen Relativitätsprinzip untergeordnet.

c) Die Aberration.

Im vorangegangenen Abschnitt ist die Zeitdifferenz, die zwischen der Uhr des ruhenden und der des bewegten Beobachters besteht, für einen besonders einfachen Fall auf den Unterschied der Richtungen zurückgeführt, in der beide denselben Punkt suchen. Dieser Richtungsunterschied ist ganz unabhängig von der Relativitätstheorie, er ist den Astronomen seit etwa 200 Jahren bekannt, und seine praktische Verwertung gehört sozusagen zum alltäglichen Handwerkszeug des Astronomen. Da diese Dinge in die ganze Denkweise der Relativitätstheorie gut einführen, durchaus leichtverständlich sind und auch meist in populär-astronomischen Schriften nicht ausreichend behandelt werden, so sei es gestattet, auf sie etwas ausführlicher einzugehen, als es unser unmittelbarer Zweck vielleicht erfordert.

Wir nehmen, um einen schon öfters verwandten Vergleich zu gebrauchen, an, jemand habe ein genau zylindrisches Rohr, etwa eine Regenröhre oder etwas ähnliches, und gehe damit im Regen spazieren. Wir setzen voraus, es herrsche völlige Windstille, so daß die Regentropfen ganz haarscharf senkrecht herunterfallen. Der Mann hat sich nun vorgenommen, sein Rohr so zu halten, daß die Tropfen völlig ungehindert hindurchfallen, ohne dabei die Rohrwände zu berühren. Er wird, wenn er selbst stillsteht, das Rohr natürlich ganz genau senkrecht halten müssen. Er fängt nun aber an zu gehen und will auch dabei noch seinen Vorsatz weiter ausführen. Hält er das Rohr nach wie vor senkrecht, so werden die Tropfen, die oben in dieses hineingelangen, wider die hintere Wand schlagen und also nicht ungehindert hindurchfallen. Neigt er aber sein Rohr nach vorn etwas im Sinne seiner Bewegung, so werden die Tropfen nicht behelligt werden.

Wieviel wird er das Rohr nach vorn senken müssen? Das wird von der Geschwindigkeit der Tropfen und von seiner eignen abhängen. Fallen die Tropfen sehr langsam, so wird eine bedeutende Neigung, fallen sie schnell, oder, was eigentlich dasselbe bedeutet, geht er nur langsam, eine geringe Senkung nötig sein. Das Verhältnis der beiden Geschwindigkeiten der Tropfenbewegung und der Vorwärtsbewegung des Beobachters bedingt also die Größe des Ablenkungswinkels. Oder nehmen wir, um ein etwas weniger harmloses Beispiel zu bilden, nun an, es schieße jemand in einen fahrenden Eisenbahnzug; die Kugel dringe zum einen Fenster hinein und verlasse den Zug durch das gegenüber liegende Fenster. Auch wenn nun senkrecht auf den Zug geschossen worden ist, so wird doch ein mitfahrender Reisender, wenn er die Lage der beiden Schußlöcher untersucht, keineswegs eine gegen die Fahrtrichtung senkrechte Richtung feststellen, weil sich eben der Zug, während die Kugel ihn durcheilte, vorwärtsbewegte. Wiederum wird die Größe der Abweichung von dem Verhältnis der beiden Geschwindigkeiten des Geschosses und des Zuges abhängen.

Machen wir nun die Anwendung: Auch wenn wir unser Fernrohr auf einen Stern richten, bewegen wir uns infolge der Erdbewegung vorwärts, während die Lichtstrahlen das Fernrohr durcheilen; wir werden das Fernrohr im Sinne unserer Bewegung nach vorn neigen müssen, und zwar um so stärker, je schneller unsere Bewegung im Vergleich zur Lichtgeschwindigkeit ist. In dem einfachsten Fall, der sowohl in den vorigen Beispielen als auch im vorangegangenen Abschnitt angenommen wurde, nämlich dem, daß die eindringende Bewegung der Regentropfen, des Geschosses oder der Lichtstrahlen auf der Richtung des Beobachters senkrecht steht, ergibt sich genau der im vorigen Abschnitt angegebene Winkel von ⅓ Minute oder dem hundertsten Teil des scheinbaren Sonnen- oder Vollmonddurchmessers. Diese dem Astronomen längst wohlvertraute Erscheinung wird als »Aberration« (Abirrung) bezeichnet.

Es ergibt sich nun Gelegenheit zu mancherlei Bemerkungen. Einmal haben wir in diesem Abschnitt die Erklärung der Aberration vom absoluten Standpunkte oder dem des »mechanischen Relativitätsprinzips« aus gegeben, während im vorigen Abschnitt das elektromagnetische Relativitätsprinzip vorausgesetzt wurde. Der wesentliche Unterschied dabei ist, daß sich die Bewegungen der Mechanik nach dem »Parallelogramm der Kräfte« oder eigentlich besser »Parallelogramm der Bewegungen« zusammensetzen, während die elektromagnetische Relativitätstheorie die Zusammensetzbarkeit der Lichtbewegung mit einer mechanischen Bewegung leugnet. Beide Theorien sind jedoch gleich gut imstande, die Tatsache der Aberration zu erklären, und führen übrigens auch quantitativ auf das gleiche Resultat.

Die zweite Bemerkung, die wir zu machen haben, ist die, daß es also außer der bekannten Raumperspektive noch eine Art »Geschwindigkeitsperspektive« gibt. Es ist ja bekannt, daß dieselbe Landschaft verschieden aussieht, je nachdem, von welchem Punkte aus man sie betrachtet. Die Lehre von der Aberration zeigt aber, daß sie auch vom nämlichen Punkte aus betrachtet ganz verschieden aussieht, je nach der Richtung und der Schnelligkeit, mit der der Beobachter den Punkt durcheilte. Die Verschiebung ist um so größer, je größer die Geschwindigkeit des Beobachters ist. Ist diese etwa gleich der des Schalles, so wäre die Aberration mit allen Hilfsmitteln moderner astronomischer Meßkunst noch gerade eben wahrnehmbar.

Vom Standpunkte des elektromagnetischen Relativitätsprinzips aus ist es ja nun eigentlich unberechtigte Willkür, den Bewegungszustand eines Beobachters schlechthin als »Ruhe«, den eines andern schlechthin als »Bewegung« zu bezeichnen. Wir dürfen eigentlich nur von ihrer relativen Bewegung gegeneinander reden und demnach auch eigentlich nur von einer »relativen« Aberration, nämlich derjenigen Aberration, die der eine Beobachter im Vergleich zum andern hat. Da wir nun aber gar keinen andern Beobachter haben, mit dem wir unsere Sternörter vergleichen könnten, so kann man wohl fragen, warum wir überhaupt von einer Aberration reden, und wie sie festgestellt werden kann. Die Antwort ist, daß die Astronomie allerdings keine Veranlassung hätte, sich mit der Aberration zu befassen, wenn die Bewegung der Erde eine geradlinig-gleichförmige und demnach die Aberration eine stets gleichbleibende Größe wäre. Infolge der Bewegung der Erde um die Sonne aber ändert sich die Richtung der Erde und mit ihr die Richtung, und Größe der Aberration, die also in Wirklichkeit auch nur eine »relative Aberration« gegen die der Sonne ist. Ihre Entdeckung war seinerzeit der erste wirklich durchschlagende Beweis für die Richtigkeit des Kopernikanischen Systems, der ja, wie uns unser erster Abschnitt zeigte, keineswegs einfach zu führen war. Was nun die Frage der absoluten Aberration anlangt, so kann man hierbei den Fixsternhimmel, weil dieser ja doch eben beobachtet werden soll, unbedenklich als ruhend ansehen. Die absolute Aberration der Sonne wäre also zu berechnen, wenn ihre Bewegung gegen den Fixsternhimmel bekannt wäre. Das ist nur in grobem Umriß der Fall. Außerdem würde sie ja auch den Ort eines jeden Sternes nur um eine ganz feste Größe ändern, was für die allermeisten astronomischen Untersuchungen, da sie ja eben nur relative Bewegungen der Sterne untereinander zum Gegenstand haben, ohne Wert wäre.

Schließlich kann man fragen, ob man denn wenigstens die relative Aberration der Erde gegen die der Sonne, die sich doch eben auf alle Sterne erstreckt, genau messen kann. Denn auch diese Messung setzt ja Richtlinien oder Richtpunkte, die nicht an der Verschiebung teilnehmen, voraus. Diese gibt es nun allerdings! Bei dem oben gegebenen Beispiel des Schusses in den Eisenbahnzug ist leicht zu sehen, daß trotz aller Verschiebung die Horizontalrichtung und daher die Horizontalebene erkennbar bleibt. Der Schuß wird nur dann als horizontal abgegeben erscheinen, wenn er es auch in Wirklichkeit ist. Dem entspricht am Himmel die Ebene der Erdbahn, die sogenannte Ekliptik, die als solche trotz aller Aberration in ihr unverändert bleibt. Ferner ist die Richtung der Rotationsachse der Erde, der sogenannte Himmelspol, von der fortschreitenden Bewegung der Erde vollständig unabhängig. Diese beiden festgebliebenen Elemente, Ekliptik und Himmelspol, gestatten also die absolute Bestimmung der relativen Aberration der Erde gegen die Sonne.

Nach dieser kleinen und hoffentlich entschuldigten Abschweifung kehren wir zum Thema zurück.

d) Ein zweites Beispiel.

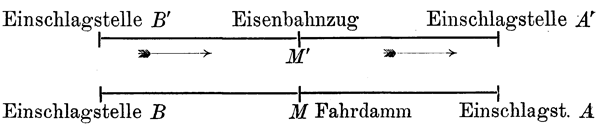
Die Blitze schlagen ein.

Die Figur stellt einen 300 000 km langen Eisenbahnzug dar, in dessen Mitte sich ein Beobachter M' befindet, der gerade an einem auf dem Bahndamm befindlichen Beobachter M vorbeifährt. Nun schlagen an beiden Enden des Zuges Blitze ein, die weiter kein Unheil anrichten, als daß sie im Zug einige Fensterscheiben zertrümmern und auf dem Bahndamm einige Furchen hinterlassen, so daß unser Zug ruhig weiterfahren kann. Nach einer halben Sekunde bietet sich uns nun folgendes Bild:

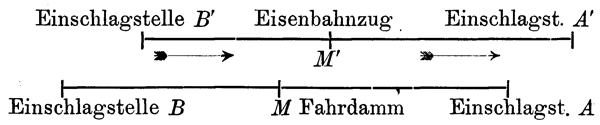
Der Blitzschein wird wahrgenommen.

Wenn M, wie wir annehmen wollen, beide Blitze gleichzeitig wahrnimmt, so ist dies für M' natürlich ausgeschlossen. Denn das von rechts herkommende Licht ist eher, das von links herkommende später in M' als in M; M' sieht also den Blitz A eher als B. An sich besagt dies natürlich noch nichts Auffallendes; denn M' wird auch ein von A kommendes Schallsignal eher wahrnehmen als ein von B ausgehendes, ohne daß dies zu einer Relativierung der Zeitmessung führt. Denn er muß sich sagen, daß er gegen die Luft bewegt ist; es steht ihm natürlich auch frei, anzunehmen, daß er stillsteht und der Wind an ihm vorbeistreicht; jedenfalls aber muß er eine größere Relativgeschwindigkeit des Schalles von rechts als von links her annehmen und ist nicht berechtigt, aus der ungleichzeitigen Ankunft der Schallsignale auf die Ungleichzeitigkeit ihrer Entstehung zu schließen. Ganz anders der mit optischen Signalen arbeitende Beobachter! Für ihn gibt es eben kein der Luft entsprechendes, einen bestimmten Bewegungszustand einnehmendes System für die Lichtfortpflanzung; er hat vielmehr gewissenhaft seinen Michelson-Versuch angestellt und weiß, daß das Licht sich für ihn nach beiden Richtungen gleich schnell fortpflanzt. Als Ausgangspunkt der Lichtwellen aber wird er sich natürlich an die von ihm durchaus gleich weit entfernten zerbrochenen Fensterscheiben A' und B' halten; denn die ungleiche Entfernung der Bahndammfurchen A und B führt er auf eine Bewegung des Bahndamms zurück, falls er sie überhaupt bemerkt; denn er ist nicht verpflichtet, zum Fenster hinauszusehen. Hieraus aber ergibt sich, daß M' eine durchaus gleiche Zeit für die Fortpflanzungsdauer beider Blitzscheine annehmen muß; er ist somit berechtigt, aus der ungleichzeitigen Ankunft der Lichtsignale auch auf ihre ungleichzeitige Aussendung zu schließen. Zwei Ereignisse, die für M gleichzeitig sind, sind es für M' nicht.

In zahlreichen mir bekannten populären Darstellungen wird dem Leser der Schluß zugeschoben, als sei der Beobachter berechtigt, von der ungleichzeitigen Wahrnehmung der Signale ohne weiteres auf ihren ungleichzeitigen Abgang zu schließen. Vor solcher Übereilung seien unsere Leser hiermit gewarnt!

6. Korrekturen und Zusammenfassung.

Nachdem wir die Einsteinsche Relativierung des Raumes und der Zeit kennen gelernt haben, ist es nun die höchste Zeit, mit allem Nachdruck darauf hinzuweisen, daß sie keinesfalls getrennt voneinander gedacht werden dürfen. Insofern diese Trennung bisher teils ausdrücklich vorausgesetzt, teils stillschweigend beim Leser geduldet wurde, litt unsere Darstellung an Mängeln, die wir nun nachträglich korrigieren oder doch wenigstens klarstellen wollen. Wir kehren zunächst zu dem wichtigen Bild des abfahrenden Eisenbahnzugs auf S. 19 zurück. Die entscheidende Grundtatsache der ganzen Relativitätstheorie, die zugleich für unsere Anschauung eine so unüberwindliche Schwierigkeit bot, war die folgende: Wird im Augenblick, wo der letzte Wagen des 300 000 km langen Eisenbahnzugs vorbeifährt, an seinem letzten Wagen ein Zeichen gegeben, ganz gleich, ob auf seinem Trittbrett oder dicht daneben auf dem Boden, so stellt sowohl der auf den Trittbrettern des fahrenden Zugs als auch der daneben auf dem Boden messende Beobachter fest, daß das Licht in einer Sekunde 300 000 km zurückgelegt habe. Dabei ist der Zug in dieser Sekunde weitergefahren! Mag man nun diese Behauptung für glaubhaft halten oder nicht, wir betrachten sie als durch Versuch bewiesen. Und wenn das Experiment gesprochen hat, so ist für den Naturforscher, zumal für den Theoretiker – der Experimentator kann ja immerhin nochmal nachprüfen –, die Frage erledigt. Wir versuchten uns nun das Resultat zunächst im Anschluß an Lorentz dadurch klarzumachen, daß wir sagten, der Eisenbahnzug hat sich zusammengezogen. Wenn dies aber der einzige Erklärungsgrund ist, so würde es einfach heißen, daß die Lokomotive des Zuges stehen geblieben sei und sich nur die Wagen nach vorn zusammengedrängt haben. Nur unter dieser Voraussetzung würde der Endpunkt der 300 000 km des Mitfahrenden zugleich der Endpunkt der 300 000 km des Stehengebliebenen sein. Man überzeugt sich aber leicht, daß diese Anschauungsweise ganz unmöglich ist und an inneren Widersprüchen leidet. Denn nehmen wir nun an, daß das Signal gegen die Fahrtrichtung, diesmal etwa von der Lokomotive aus, abgegeben werde und sehen zunächst einmal von jeder Verkürzung ab, so wird der ruhende Beobachter feststellen, daß nach einer Sekunde das Licht nicht etwa nur beim letzten Wagen angelangt ist, sondern sogar schon darüber hinaus, denn der letzte Wagen hat sich innerhalb der Beobachtungssekunde nach vorn geschoben. Wollen wir die Frage nach der bisherigen Methode erledigen, so müßten wir nunmehr sogar Dehnung des Zuges annehmen, derart, daß der letzte Wagen stehen geblieben und nur die Lokomotive nach vorn gefahren ist. Nun liegt der Widerspruch auf der Hand: Wenn der Zug abfährt, kann man doch nicht wissen, ob das Signal in seiner Fahrtrichtung oder gegen sie abgegeben wird. Ja, es hindert uns sogar niemand, anzunehmen, daß gleichzeitig Lichtblitze in beiden entgegengesetzten Richtungen erfolgen, und unser Zug würde, wenn er sprechen könnte, zu uns sagen: Ich würde euch ja herzlich gern den Gefallen tun und meine Gestalt verändern und verzerren, soviel ihr wollt; aber Dehnung und Kürzung in derselben Sekunde, das ist zuviel verlangt!

Das Problem ist eben auf rein geometrischem Wege nicht lösbar! Es wird dies erst mit Zuhilfenahme der Zeitbetrachtung. Wir lassen das Signal wieder wie zuerst von hinten nach vorn gehen. Wir nehmen eine viel geringere Aus der Betrachtungsweise der S. 18 u. 19 würde sich z. B. eine Verkürzung des Erddurchmessers von über 1 km ergeben, während sie nach der richtigen Theorie nur 6,5 cm beträgt. Verkürzung wie eben an, so daß also auch die Lokomotive weitergefahren ist. Sie ist nun natürlich von der Abfahrtsstelle weiter als 300 000 km entfernt, und der Widerspruch, daß trotzdem, wie der fahrende Beobachter feststellt, das Licht bis zu ihr vorgedrungen sei, scheint schlimmer denn je! Aber nun nehmen wir an, daß die Uhr des fahrenden Beobachters, die am Anfange der Beobachtungssekunde mit der des ruhenden übereinstimmte, im Laufe dieser Zeitspanne zurückgeblieben sei, also nunmehr nachgehe. Dann wird natürlich der stehen gebliebene Beobachter dem fahrenden zurufen: Lieber Freund! Du mißt und mißt und merkst gar nicht, daß die verabredete Sekunde längst verflossen ist! Meine Uhr ist abgelaufen! Ich will dir ja an sich natürlich gerne glauben, daß das Licht bis zu deiner Lokomotive vorgedrungen sei, aber mache mir nicht weis, daß das im Verlauf einer Sekunde geschehen ist.

Entsprechend liegt die Sache bei unserm auf S. 28 u. 29 gebrauchten Bild der konzentrisch fortschreitenden Raumwellen des Lichtes. Jeder Beobachter sieht doch, wie nach und nach jeder Punkt des Raumes beleuchtet wird. Wartet er nur genügend lange, so hat für ihn ein jeder Punkt des ganzen unendlichen Universums sein Teil Licht abbekommen. Spricht er davon, daß das Licht sich kugelförmig ausbreite, so meint er natürlich, daß gleichzeitig die Punkte einer Kugeloberfläche von der Lichtbewegung erfaßt seien. Aber eben der Begriff der Gleichzeitigkeit ist doch, wie der vorige Abschnitt zeigte, kein absoluter, sondern verschieden für die verschiedenen Beobachter. Was dem einen von ihnen als gleichzeitig erscheint, braucht es für den andern noch nicht zu sein. Würde also der eine unserer Beobachter, um seinen Kollegen zu überführen, etwa versuchen, zu einer ganz bestimmten Zeit die Lichtbewegung, um in aller Ruhe messen zu können, anzuhalten, und alsdann zu jenem sagen: Nun siehst du doch wohl, daß das Licht eine Kugel um mich als Mittelpunkt beschrieben hat, so würde dieser vermutlich kaltlächelnd erwidern: Lieber Freund! Daß das Licht an den von dir markierten Punkten angelangt ist, das bezweifle ich keineswegs, aber eben nicht gleichzeitig! Meiner Meinung nach war es in dieser Gegend der von dir abgesteckten Kugel eher als in jener! Und was deinen Zollstock betrifft, darüber habe ich nach wie vor meine eigne Meinung!

Wenn wir die Zerrungen des Raumes und der Zeit getrennt voneinander betrachtet haben, so geschah dies nur der leichteren Verständigung wegen. Tatsächlich sind sie nicht unabhängig voneinander, sondern im Gegenteil aufs engste gegenseitig bedingt. Nehmen wir, um dies einzusehen, einmal an, es sei vorläufig nur die Relativierung der Raummessung zugestanden. Nun sehen wir einfach nach unserer Taschenuhr, die wir uns freilich so weit entfernt vorstellen, daß wir die abgelesene Zeit nicht ohne weiteres als die richtige annehmen dürfen, vielmehr zu ihr noch die Zeit addieren müssen, die das Licht vom Zifferblatt bis in unser Auge gebraucht hat. Die Größe dieser Korrektur wird sich natürlich nach der Entfernung der Uhr richten, und für zwei Beobachter, die eben diese Entfernung verschieden abschätzen, auch verschieden ausfallen. Wir sehen also: Aus der Relativierung der Raumgrößen folgt notwendig die relative Auffassung der Zeitmessung. Nun umgekehrt! Man habe uns zwar die relative Auffassung der Zeit zugegeben, aber noch nicht die des Raumes. Wir erinnern uns nun, wie auf S. 23 die Länge des fahrenden Zuges gemessen wurde dadurch, daß zur genau gleichen Zeit sein Anfang und Ende durch Kreidestriche auf dem Bahndamm bestimmt wurden. Entstehen nun Meinungsverschiedenheiten darüber, was als gleichzeitig zu betrachten ist, so werden, wegen der ständigen Weiterbewegung des Zuges, die Kreidestriche auf verschiedenen Punkten des Bahndamms erfolgen und eine verschiedene Längenangabe wird die Folge sein. Ergebnis: Aus der Relativierung der Zeitgrößen folgt notwendig die relative Auffassung der Raummessung. Diese Verquickung der Änderung des Raum- mit der des Zeitmaßes bietet ohne Frage eine wesentliche Schwierigkeit beim Verständnis der Relativitätstheorie.

Die allererste Aufgabe der Relativitätstheorie ist es, allgemein die Beziehungen anzugeben, die zwischen den Raum- und Zeitmaßen irgend zweier relativ geradlinig-gleichförmig gegeneinander bewegten Systeme bestehen. Solche Beziehungen, sogenannte »Transformationsgleichungen«, abzuleiten, war bereits Lorentz gelungen. Einstein gelang es, diese Formeln auf theoretisch-deduktivem Wege allein aus zwei Voraussetzungen heraus abzuleiten:

1. Der Konstanz der Lichtgeschwindigkeit für alle Beobachter. Sie gilt als durch die Erfahrung hinreichend gesichert.

2. Der Relativität aller geradlinig-gleichförmigen Bewegungen.

Alle in dieser Weise gegeneinander bewegten Systeme gelten als völlig gleichberechtigt. Es ist unmöglich, etwa zu entscheiden, welches von ihnen das »ruhende« ist. Alle Naturgesetze nehmen sich von jedem von ihnen betrachtet völlig gleichartig aus. Insbesondere muß der Übergang, eben die Transformationsgleichungen, vom ersten System ins zweite genau so sein wie vom zweiten System ins erste.

Die rein rechnerischen mathematischen Schwierigkeiten sind nun keineswegs so bedeutend, wie sie auf den ersten Blick wohl scheinen möchten, wenigstens was die allerersten hier skizzierten Grundlagen der Theorie anlangt. Sie kommen erst durch den immer aufs neue entbrennenden Kampf zwischen dem »Anschaulichkeit« verlangenden Geiste und der auf unanschauliche Tatsachen und noch abstraktere Rechnung gegründeten Theorie, die diese Anschaulichkeit als unmöglich zurückweist.

Schließlich behandeln wir noch eine Frage, die immer bei solchen Erörterungen auftaucht, und die sich auch der Leser schon gestellt haben wird: Kann sich ein System mit Lichtgeschwindigkeit oder gar noch größerer Geschwindigkeit bewegen? Die Antwort darauf ist nicht schwer. Nehmen wir an, unser Zug bewege sich mit größerer als Lichtgeschwindigkeit, so müßte jetzt natürlich ein am Schlußwagen abgegebenes Lichtsignal sich für den mitbewegten Beobachter auf dem Zug verbreiten, für den ruhenden jedoch immer hinter dem Zug zurückbleiben, und zwar um so mehr, je weiter der Zug fährt. Dieser Widerspruch ist mit keinerlei Mitteln heilbar, es bleibt nur noch der eine Schluß übrig, daß es solche Geschwindigkeiten nicht geben kann. Kein Körper kann sich schneller oder auch nur ebenso schnell wie das Licht bewegen. – Die Geschwindigkeiten der Himmelskörper betragen gewöhnlich 10-30 km in der Sekunde, doch kommen ausnahmsweise auch solche von mehreren hundert Kilometern vor. Sie erreichen also kaum 1/1000 der Lichtgeschwindigkeit. Viel schneller bewegen sich die Korpuskeln der Kathodenstrahlen, und noch schneller die β-Strahlen des Radiums, welch letztere bis zu etwa 99 % der Lichtgeschwindigkeit erreichen. Diese selbst verhält sich etwa wie der absolute Nullpunkt der Temperatur, sie wird nie erreicht, so sehr man sich ihr zu nähern scheint. Sollte wirklich einmal eine größere als Lichtgeschwindigkeit festgestellt werden, so würde dies ohne Frage einen Umsturz unserer ganzen theoretischen Physik zur Folge haben. Doch ist hierzu zu bemerken, daß solche Geschwindigkeiten ja nicht unmittelbar beobachtet, sondern aus der Theorie erschlossen sind. Man würde sich also alsdann zweifellos eher entschließen, irgendeinen andern Punkt der Theorie zu ändern, solange dies irgend möglich wäre, um der angedeuteten Folgerung auszuweichen. Von hier aus kommen wir auch leicht zu einer andern Folgerung unserer Lehre. Die Unmöglichkeit, die Lichtgeschwindigkeit zu erreichen, kann sich nicht sozusagen plötzlich herausstellen. Man sieht leicht, daß es nicht so sein kann, daß ein Körper ebenso leicht, wie es nach der bisherigen Mechanik der Fall sein müßte, 99 % der Lichtgeschwindigkeit erreichen kann und die Unmöglichkeit sich erst beim letzten Prozent herausstellt. Ein vermehrter Widerstand muß sich also von Anfang an bemerkbar machen. Den Widerstand, den ein Körper der Vermehrung seiner Geschwindigkeit entgegensetzt, nennen wir seine Masse, und wir sehen: Die Masse eines Körpers, die man bisher als absolute Konstante betrachtete, wächst mit seiner Geschwindigkeit. Bei den gewöhnlichen, im Vergleich zum Licht ja außerordentlich langsamen Bewegungen merkt man dies freilich nicht. Für die schnellen Elektronenbewegungen aber, wie wir sie in den Kathoden- und β-Radiumstrahlen kennen, ist dieser Satz aufs beste bestätigt.

7. Die vierdimensionale »Veranschaulichung« Minkowskis.

Dieser Abschnitt, der dem mathematisch nicht vorgebildeten Leser einige Schwierigkeiten machen wird, ist für das Folgende nicht unbedingt notwendig; dasselbe gilt auch von Abschnitt 15.

In gewisser Art ist eine Veranschaulichung, deren Möglichkeit wir schon mehrfach leugneten, dem leider zu früh verstorbenen Göttinger Mathematiker Minkowski in seinem 1908 zu Köln gehaltenen Vortrag doch gelungen, der, wiewohl er rein physikalisch über Einstein nicht hinausging, wegen seiner ganz außerordentlichen mathematischen Schönheit zu den klassischen Schriften der Relativitätstheorie gezählt wird und seinerzeit die Relativitätstheorie unter den Mathematikern erst populär gemacht hat.

Minkowski versuchte eine Darstellung im vierdimensionalen Raum. Dieser erscheint ja nun freilich dem Nichtmathematiker als der Gipfelpunkt abstrakter Verstiegenheit. Indessen hat es damit folgende, ziemlich einfache Bewandtnis. Eine gerade Linie ist für den Mathematiker eine Gelegenheit, an jeden ihrer Punkte eine Zahl anzuschreiben, in der Art etwa, wie wir dies von einem Metermaßstab, einer Barometer- oder Thermometerröhre oder so viel ähnlichen Gelegenheiten gewöhnt sind. Ebenso bedeutet ihm eine Ebene die Möglichkeit, zwei Zahlen, die er sich etwa auf zwei aufeinander senkrecht stehenden Linien, sog. »Achsen«, aufgetragen denkt, in jeder beliebigen Weise zu gruppieren. Jeder Punkt der Ebene entspricht einem Zahlenpaar, nämlich den Abständen des Punktes von den beiden Achsen; der Raum schließlich gibt ihm die Möglichkeit, die Zusammennahme je dreier Zahlen, etwa von Länge, Breite und Höhe, durch einen einzigen Punkt zu veranschaulichen. Wird nun in dieser Weise fortgefahren und je vier Zahlen zueinander gruppiert, so fehlt hierfür freilich die geometrische räumliche Veranschaulichung. Aber nun kann umgekehrt die Zusammenstellung der Zahlen, die weiterhin genau so erfolgt wie in der Geraden, Ebene und dem gewöhnlichen Raum, ein Bild für den vierdimensionalen Raum abgeben, bei dem man eben nur stets vier Zahlen gruppiert statt der einen, zwei oder drei Zahlen in den niederen Gebilden. Dort hilft die Raumanschauung dem Zahlengebilde nach, hier gibt umgekehrt das Zahlengebilde die Stütze ab für die sonst fehlende Raumanschauung.

Innerhalb dieses vierdimensionalen Zahlengebildes, das der Mathematiker als »vierdimensionalen Raum« anspricht, das freilich dem Nichtmathematiker selbst wieder reichlich abstrakt und unanschaulich vorkommt, gelang es nun Minkowski, die bisher schmerzlich vermißte volle Anschaulichkeit zu erreichen. Insbesondere trat die enge Zusammengehörigkeit zwischen Raum- und Zeitgrößen, die hervorzuheben auch wir uns bemüht haben, ganz besonders plastisch hervor. Die Zeit erscheint bei ihm als Achse, gleichartig den Raumachsen, so daß ihr von vornherein jede Besonderheit genommen ist. Von einem Raumpunkt an sich und ebenso von einem Zeitpunkt an sich zu reden, hat nur innerhalb eines gegebenen Systems, also nicht ohne weiteres, einen bestimmten Sinn. Unmittelbar gegeben sind ja weder Raumpunkte noch Zeitpunkte, sondern Ereignisse, die zu ihrer Bestimmung die Angabe sowohl des Raumes als auch der Zeit benötigen. Machen wir uns das Weitere an einem Beispiel klar!

Ich nehme in jede Hand einen Federhalter und mache damit auf zwei Stücke Papier, die etwa 1 m weit voneinander entfernt liegen, fast gleichzeitig einen kleinen Klecks. Nach der alten Anschauung würde man nun natürlich sagen: Sind diese beiden Ereignisse nicht haarscharf gleichzeitig, so sind sie eben zeitlich und räumlich getrennt. Wir können die Sache aber auch anders ansehen! Nehmen wir an, ich habe den einen Klecks 1/100 Sekunde früher gemacht als den andern! »Räumlich« getrennt sind die beiden Ereignisse freilich, solange ich das System des Tisches als ruhend annehme, was hier natürlich in der Tat sehr naheliegt. Es hindert mich aber niemand, ein System von solcher Relativgeschwindigkeit gegen den Tisch anzunehmen, daß sich in der zwischen beiden Klecksen verfließenden Zeit ein Punkt gerade von dem einen Klecks zum andern hinbewegt hat, und in diesem System sind die Kleckse natürlich an demselben Ort, hingegen zu verschiedener Zeit erfolgt. Nehmen wir an, auf einem vorüberziehenden schmalen Streifen Papier, wie es etwa zu einem Morsetelegramm benutzt wird, habe ein kleiner Beobachter gestanden; der würde natürlich berichten: Ich blieb ruhig auf meinem Platz stehen, aber kurz hintereinander flog mir zweimal die Tinte um die Ohren. Daß sie auf verschiedene Teile des Schreibtischs niederfiel, lag natürlich daran, daß dieser sich mit großer Geschwindigkeit unter mir wegbewegte! Für diesen Beobachter wären also die Ereignisse nur durch die Zeit, nicht durch den Raum getrennt. Dieser Fall ist nun nicht der einzig mögliche. Nehmen wir an, die beiden durch 1 m voneinander getrennten Ereignisse hätten so kurz nacheinander stattgefunden, daß zwischen ihnen nur der billionste Teil einer Sekunde verstrichen wäre. Jetzt kann man kein System angeben, das sich in so kurzer Zeit von dem einen Punkt zu dem andern bewegt haben könnte, weil dazu größere als Lichtgeschwindigkeit erforderlich wäre, mit der sich kein System bewegen kann. Wohl aber kann man jetzt, was wir hier natürlich nicht beweisen können, ein System angeben, in dem die beiden Ereignisse genau gleichzeitig erfolgen, also nur räumlich voneinander getrennt sind. Minkowski würde sagen: Diese beiden Ereignisse sind durch eine »raumartige« Entfernung voneinander getrennt, während er die beiden ersten Ereignisse durch eine »zeitartige« Entfernung voneinander getrennt nennt. Es ist leicht zu sehen, daß der Vorgang der Lichtausbreitung die Grenze zwischen »raumartigen« und »zeitartigen« Entfernungen bildet.

Daß wir es im gewöhnlichen Leben für zweckmäßig halten, von räumlicher und zeitlicher Entfernung zweier Ereignisse zu sprechen, das könnte man etwa damit vergleichen, daß es, wenn die Straßenzüge gerade so angelegt sind, auch sehr praktisch sein kann, erst nach Süden und dann nach Osten zu gehen, statt auf dem nächsten Wege nach Südosten.

Alle diese und noch eine große Menge anderer Beziehungen treten an dem vierdimensionalen Modell Minkowskis in unmittelbarer Anschaulichkeit hervor. Sie veranlaßten ihn zu dem berühmten Ausspruch: Von Stund' an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken, und nur noch eine Art Union der beiden soll Selbständigkeit bewahren.

So treffend dieser Ausspruch auch ist, so hat doch M. Schlick, wie mir scheint, ebenso treffend hinzugefügt, daß auf Grund der alsbald zu besprechenden allgemeinen Relativitätstheorie auch diese Union noch zum Schatten, zur Abstraktion geworden ist, und daß nur die Einheit von Raum, Zeit und Dingen zusammen eine selbständige Wirklichkeit besitzt. Denn im Gegensatz zur speziellen wird es das Wesen der allgemeinen Relativitätstheorie sein, daß man nicht einmal solch ganz allgemeines Schema wie das Minkowskische aufstellen kann, ehe man die Dinge, die Ereignisse kennt, die damit beschrieben werden sollen.

Eine, wie mir scheint, vortreffliche Veranschaulichung der Minkowskischen Darstellung bietet auch folgende Überlegung, die ich einer freundlichen Mitteilung von Herrn Prof. Böhmer (Dresden) verdanke: Durch eine photographische Aufnahme wird ein Teil der dreidimensionalen Welt auf eine ebene Fläche abgebildet. Nach Art eines Films denken wir uns nun irgendwelche Bewegungsvorgänge durch eine große Zahl schnell folgender Aufnahmen auf die Platte gebracht. Die entstandenen zahlreichen Bilder werden alsdann wie die Blätter eines Buches aufeinander gelegt, so daß ein rechteckiger Block entsteht. Die Schichtung sei so genau vorgenommen, daß derselbe Raumpunkt in allen Abbildungen ganz genau hintereinander zu liegen kommt. Durch diesen unseren Filmblock machen wir nun mehrere verschiedenartige Schnitte; erfolgt ein solcher Schnitt genau in der Ebene eines der den Block bildenden Blätter, so sehen wir vor uns ein Bild des Raumes, wie er sich zu einer ganz bestimmten Zeit uns darbot. Schneiden wir hingegen genau senkrecht zu dieser Ebene alle hintereinander liegenden Blätter durch, so liefert uns die nun entstandene Schnittfläche sozusagen die Geschichte einer Raumlinie; denn die nacheinander durchschnittenen Filmblätter zeigen uns, wie unsere Linie zu den verschiedenen Aufnahmezeiten ausgesehen hat, die ganze Schnittfläche also, wie sie sich allmählich veränderte. Wir können uns nun davon überzeugen, daß beide auf den ersten Blick so verschiedene Schnittarten nicht absolut verschieden sind, sondern ineinander übergehen. Denn wie wird ein Beobachter schneiden müssen, der relativ zum aufnehmenden Beobachter bewegt ist, und der nun seinerseits die Geschichte einer Raumlinie verfolgen will? Da er sich bewegt, verschiebt sich, ihm unbewußt, die von ihm betrachtete Linie mit, vielmehr er identifiziert im Laufe der Zeit andere Linien mit der zuerst betrachteten als der ruhende Beobachter; und da wir die Bewegung des zweiten Beobachters als geradlinig-gleichförmig annehmen, so sehen wir leicht, daß wir nun in einer Ebene schneiden müssen, die nicht senkrecht zu den Filmblättern steht und deren Winkel sich von einem rechten um so mehr unterscheiden wird, je schneller der zweite Beobachter gegen den ersten bewegt war. Aber auch die die gleichzeitige Lage der Welt darstellenden Bilder sind für den bewegten Beobachter andere als für den ruhenden. Denn wie im fünften Kapitel von der Relativierung der Zeit ausführlich gezeigt worden ist, empfindet er nicht die Ereignisse als gleichzeitig, die der ruhende Beobachter als solche bezeichnet, und es ist leicht zu sehen, daß die Zeitdifferenz um so mehr anwachsen wird, je weiter entfernt die zu vergleichenden Ereignisse von dem Beobachter liegen. So mußte in unserem obigen Beispiel Seite 37 eine Entfernung von 6 Lichtjahren angenommen werden, um 1 Sekunde Zeitdifferenz zu erhalten. Bei einer Entfernung von 12 Lichtjahren würden sich also 2 Sekunden Zeitdifferenz ergeben, bei 18 Lichtjahren 3 Sekunden usw. Folgen etwa 10 Filmaufnahmen in der Sekunde, so muß, um ein gleichzeitiges Bild der Welt zu erhalten, so schräg geschnitten werden, daß für je 6 Lichtjahre seitlicher Verschiebung 10 Filmblätter durchschnitten werden. Man sieht leicht, daß der Gleichzeitigkeitsschnitt um so schräger, d. h. in um so größerem Winkel gegen die Richtung der Filmblätter geführt werden muß, je schneller die Relativbewegung des Beobachters ist. Auf diese Weise sieht man, daß die ursprünglich als gänzlich verschiedenartig empfundenen Schnitte parallel zu den Filmaufnahmen und senkrecht zu ihnen, von denen die erstere Art die gleichzeitige Lage der Welt, die zweite die Geschichte einer Raumlinie darstellt, stetig ineinander übergehen. Eine Grenze für die Schrägheit beider Arten von Schnitten bildet wieder die Lichtgeschwindigkeit, die der bewegte Beobachter nicht erreichen oder gar überschreiten kann. Wir können hier nicht näher ausführen, wie durch dieses glücklich gewählte Modell alle wesentlichen Eigenschaften der Minkowskischen Relativitätsgeometrie veranschaulicht werden können. Es ist kaum nötig hinzuzufügen, daß Minkowski nun nicht die Welt photographieren und dadurch ihre drei Dimensionen auf zweidimensionale Bilder projizieren will, sondern sich die dreidimensionalen Welten selbst aneinandergefügt denkt, was natürlich nur in einer vierten Dimension möglich ist. Das Modell zeigt eben, wie durch das Hintereinanderfügen der zweidimensionalen Aufnahmen ein dreidimensionaler Block entsteht, also eine neue Dimension, nämlich die die Zeit darstellende, hinzukommt, und diese Dimension weist gegenüber den übrigen keine grundsätzliche Verschiedenheit auf Eine besonders ergötzliche Darstellung der Zeit als vierter Raumkoordinate findet sich in den »Kleinen Schriften« von Dr. Mises (Gustav Theodor Fechner), Leipzig 1875, Breitkopf & Härtel. (Nach einer freundlichen Mitteilung von Herrn Gymnasialdirektor Hauck, Hirschberg.).

Überblickt man die ganze Vorstellungswelt Minkowskis, so wird man ganz unwillkürlich an das Wort erinnert, das Richard Wagner den Gurnemanz zum jugendlichen Parsifal sprechen läßt: Du siehst, mein Sohn, zum Raum wird hier die Zeit.

8. Philosophisches Schlußwort zur »speziellen Relativitätstheorie«.

Die sogenannte »spezielle Relativitätstheorie«, die wir in grobem Umriß skizziert haben, hat in der gesamten wissenschaftlichen Welt und sogar noch darüber hinaus allenthalben das größte Aufsehen erregt, weil sie an den Grundlagen unserer Raum- und Zeitauffassung rüttelt. Niemand hatte bisher daran gedacht, daß einer Angabe wie dieser: Diese auf einem völlig starren Stab angebrachte Strecke ist 10 cm lang, eine andere als eine absolute Bedeutung zukommen könne. Ihre Richtigkeit oder Nichtrichtigkeit etwa abhängig zu denken von irgendwelchen Umständen, beispielsweise dem Bewegungszustand dessen, der das Urteil abgibt, war niemand in den Sinn gekommen. Ebensowenig hat es jemand für möglich gehalten, daß die Frage, ob zwei Ereignisse gleichzeitig stattfinden, von zwei Beobachtern verschieden beantwortet werden könnte oder daß sogar die Reihenfolge zweier Ereignisse von ihnen in umgekehrter Weise angesetzt werden könnte. Die Gründe, die die Relativitätstheorie zu ihrem geradezu revolutionären Vorgehen veranlaßte, sind wiederholt hervorgehoben. Die drei Grundsätze:

1. die absolute Konstanz der Lichtgeschwindigkeit für jeden Beobachter,

2. die Relativität aller geradlinig-gleichförmig gegeneinander bewegten Systeme,

3. die Konstanz unserer Raum- und Zeitmaße für alle Systeme sind miteinander unvereinbar, sie führen zu mathematischen Widersprüchen, die schlechthin unerträglich sind. Da man die beiden ersten Grundsätze vor allem aus Gründen der experimentellen Erfahrung, daneben aber auch aus Gründen ursprünglicher philosophischer Überzeugung nicht aufgeben konnte, so blieb nur übrig, auf den dritten zu verzichten, für den sich Gründe von gleicher Wucht jedenfalls nicht geltend machen ließen.

Es ist jedoch darauf hinzuweisen, daß die Relativierung der Zeit- und der Raummessung mit der Relativierung des Raum- und Zeitbegriffs noch nicht ohne weiteres gleichbedeutend ist. Für den Physiker sind Raum und Zeit Hilfsgrößen, die er braucht wie andere, um die Erscheinungen zu beschreiben. Ob sie weiter nichts sind, darüber hat nicht er in erster Linie zu entscheiden.

Wenn Mephistopheles sagt:

Daran erkenn' ich den gelehrten Herrn!
Was ihr nicht tastet, steht euch meilenfern!
Was ihr nicht faßt, das fehlt euch ganz und gar!
Was ihr nicht rechnet, glaubt ihr, sei nicht wahr!
Was ihr nicht wägt, hat für euch kein Gewicht;
Was ihr nicht münzt, das, meint ihr, gelte nicht,

so wird der Physiker diese Worte, abgesehen von dem in ihnen liegenden Spott, der wohl nicht nur der Meinung Mephistopheles', sondern auch der Goethes entsprach, und abgesehen von dem »Münzen«, das nie seine Sache war, als durchaus berechtigt und für seine Auffassung kennzeichnend anerkennen müssen. Dasselbe drückt Planck, einer unserer ersten Physiker, einmal positiv aus: Was ich messen kann, das existiert auch. In der Tat bedeutet für den Physiker das »Gewicht« lediglich die Zahl, die er an der Wage abliest, die Temperatur die Zahl, die das Thermometer anzeigt, die elektrische Stromstärke die vom Amperemeter gelieferte. Und in ganz gleicher Weise ist für ihn der Raum ausschließlich die Möglichkeit, den Metermaßstab anzulegen, die Zeit das Gehäuse für seine Uhr und weiter nichts. Die hinter diesen Begriffen stehenden Anschauungen haben für ihn, wie schon S. 25 ff. erwähnt, durchaus nur heuristischen und didaktischen Wert. Die Erfolge der Physik und der von ihr abhängigen Technik, die die jeder andern menschlichen Tätigkeit weit in Schatten stellen, haben die Richtigkeit dieser Prinzipien für die Physik überzeugend erwiesen.

Aber was für Begriffe wie Gewicht, Temperatur und Stromstärke, die eben ausschließlich physikalische Begriffe sind, bereitwillig zugestanden werden wird, gilt noch nicht ohne weiteres für allgemeine Begriffe wie Raum und Zeit, die nicht Spezialeigentum der Physiker sind. Die Frage, ob man nicht berechtigt sei, neben dem empirischen Raum der Physiker den alten absoluten Raum, etwa für die Zwecke mathematischer und philosophischer Spekulation, aufrechtzuerhalten, wird sich jedenfalls aufwerfen lassen. Freilich wäre dann doch sein Hauptwert, nämlich der, die Grundlage abzugeben nicht nur für die Spekulation und die innere Anschauung, sondern auch für jede empirische Forschung, unwiederbringlich dahin. Und damit kommen wir zum letzten Punkt:

Das Verhältnis empirischer Forschung und philosophischer Weltanschauung ist nicht wechselseitig dasselbe. Zwar ziemt es der empirischen Wissenschaft, in Fühlung mit der Philosophie zu bleiben, von dorther Anregung und Zusammenhang mit andern Bestrebungen zu empfangen. So ist auch beispielsweise von Mach das Relativitätsprinzip aus philosophischer Überzeugung heraus schon vor Einstein gefordert worden. Aber Ziel und Grundrichtung ihrer Forschung kann jede Wissenschaft nur aus ihren eignen Gesetzen heraus empfangen und nur durch ihre Erfolge begründen. Umgekehrt wird die Philosophie aber an den Resultaten der Einzelwissenschaft nicht vorübergehen können. Sind diese groß und bedeutend genug, so wird eine gesunde Philosophie sie in sich aufnehmen, wenn auch vielleicht nach eigentümlicher Ummodelung und Umschmelzung, und zwar auch selbst dann, wenn sie noch nicht durch die Gründe absolut bindender Logik dazu gezwungen wird. Wenn also die Relativitätstheorie, wie es jetzt den Anschein hat, ein neues und dauerndes Fundament für die Physik abgeben wird, so werden auch unsere philosophischen Anschauungen von Raum und Zeit davon nicht unbeeinflußt bleiben können.