
|
||||||||||||||
| Autoren | ∞ | Werke | ∞ | Neu | ∞ | Information | ∞ | Shop | ∞ | Lesetips | ∞ | Textquelle | ∞ | |
Anzeige. Gutenberg Edition 16. 2. vermehrte und verbesserte Auflage. Alle Werke aus dem Projekt Gutenberg-DE. Mit zusätzlichen E-Books. Eine einmalige Bibliothek. +++ Information und Bestellung in unserem Shop +++
Die erste Frage, welche aus den in der beschriebenen Weise angestellten Untersuchungen eine Antwort erwartet, ist nach den Erörterungen von §§ 7 und 8 die nach der Natur der gewonnenen Durchschnittszahlen. Sind die immerhin schwankenden Zeiten, welche erforderlich waren, um Reihen von bestimmter Länge unter möglichst gleichen Umständen gerade auswendig zu lernen, so gruppiert, dass man ihre Mittelwerte mit Wahrscheinlichkeit als Maßzahlen im physikalischen Sinne ansehen darf oder nicht?
Geschehen die Versuche in der oben auseinandergesetzten Art, sodass nämlich immer mehrere Reihen unmittelbar hintereinander gelernt werden, so wird man bei den Zeiten, die für das Lernen der einzelnen Reihen erforderlich waren, eine solche Gruppierung von vornherein nicht wohl erwarten dürfen. Denn bei längerer Dauer des Lernens treten bei den einzelnen Reihen variable Bedingungen ins Spiel, deren Schwankungen wir, nach unserer Kenntnis von ihnen, nicht als symmetrisch um einen Mittelwert voraussetzen können. Die Gruppierung der Resultate muß dadurch ebenfalls eine unsymmetrische werden und kann also dem Fehlergesetz nicht entsprechen. Solche Bedingungen sind z. B. die abnehmende geistige Frische, die zuerst sehr schnell, dann immer langsamer einer gewissen Ermüdung Platz macht, sodann die Schwankungen der Aufmerksamkeit. Die Verlangsamung des Lernens durch eine außergewöhnliche Zerstreuung kennt sozusagen keine Grenzen; die Lernzeit einer Reihe kann durch sie gelegentlich auf das doppelte und mehr ihres mittleren Betrages gesteigert werden. Der entgegengesetzte Effekt einer außergewöhnlichen Anspannung dagegen kann, der Natur der Sache nach, ein gewisses Maß nie überschreiten; er kann nie etwa einmal die Lernzeit auf Null reduzieren.
Nimmt man dagegen Gruppen von jedesmal gleichviel unmittelbar hinter einander gelernten Reihen, so können für diese jene störenden Schwankungen als wegfallend oder beinahe wegfallend betrachtet werden. Die allmähliche Abnahme der geistigen Frische wird bei einer Gruppe ungefähr in derselben Weise geschehen wie bei einer anderen. Die Schwankungen der Aufmerksamkeit nach oben und nach unten, die während einer Viertel- oder halben Stunde unter sonst gleichen Umständen vorkommen, werden zusammengerechnet heute ungefähr denselben mittleren Effekt haben wie morgen. Man wird also nur fragen können: zeigen die Zeiten, welche für das Lernen gleicher Gruppen von Reihen erforderlich waren, die gewünschte Verteilung?
Diese Frage kann ich mit befriedigender Sicherheit bejahen. Die beiden größten Reihen von unter gleichen Umständen gewonnenen Zahlen, die ich besitze, sind zwar noch nicht groß, in dem Sinne, in dem die Theorie dies voraussetzt; sie leiden ferner an dem Übelstand, dass sie aus verhältnismäßig langen Zeitperioden stammen, in denen natürlich größere Ungleichheiten der Umstände unvermeidlich sind, allein ihre Gruppierung kommt trotzdem der von der Theorie verlangten so nahe wie man nur erwarten kann.
Die erste Versuchsreihe aus den Jahren 1879/80 umfaßt 92 Versuche. Jeder Versuch bestand in dem Lernen von acht Reihen zu 13 Silben, welches fortgesetzt wurde bis ein zweimaliges Hersagen jeder Reihe möglich war. Die dazu erforderliche Zeit betrug für alle acht Reihen zusammen, eingerechnet die Zeit des Hersagens selbst (aber natürlich nicht die Pausen s. §. 13, 4), im Mittel 1112 Sekunden mit dem wahrscheinlichen Beobachtungsfehler ± 76. Die Schwankungen der Resultate waren also verhältnismäßig sehr bedeutend: in das Intervall 1036 bis 1188 fiel nur die Hälfte der erhaltenen Zahlen, die andere Hälfte nach oben und unten darüber hinaus. Im einzelnen ist die Gruppierung der Zahlen folgende:
| Es fallen innerhalb | d. h. innerhalb der Abweichung |
Anzahl der Abweichungen | |
| gezählt | berechnet | ||
| 1/10 w | ± 7 | 6 | 5 |
| 1/6 w | ± 12 | 10 | 8,2 |
| 1/4 w | ± 19 | 13 | 12,3 |
| 1/2 w | ± 38 | 30 | 24,8 |
| w | ± 76 | 45 | 46 |
| 1/2 w | ± 114 | 61 | 63,4 |
| 2 w | ± 152 | 73 | 75,6 |
| 21/2 w | ± 190 | 84 | 83,6 |
| 3 w | ± 228 | 88 | 88 |
In dem Intervall 1/4 w bis 1/2 w findet eine kleine Anhäufung der Werte statt, die durch eine größere Leere in dem nächstfolgenden Intervall 1/2 w bis w kompensiert wird; abgesehen hiervon ist die Übereinstimmung befriedigend. Zu wünschen läßt die Symmetrie der Verteilung. Die unterhalb des Durchschnitts liegenden Werte überwiegen etwas an Zahl, die oberhalb liegenden dafür etwas an Größe der Abweichung: von den acht größten Abweichungen liegen nur zwei von dem Mittelwert nach unten. Der soeben angedeutete Einfluß der Aufmerksamkeit, deren Schwankungen bei den Einzelreihen größere Abweichungen nach oben als nach unten bewirken, ist also hier durch die Zusammenfassung mehrerer Reihen noch nicht ganz kompensiert worden.
Erheblich verbessert zeigt sich die Sicherheit der Beobachtungen und die Übereinstimmung ihrer Verteilung mit der theoretisch geforderten bei der zweiten größeren Versuchsreihe. Dieselbe umfaßt die Resultate von 84 Versuchen aus den Jahren 1883/84. Jeder Versuch bestand in dem Lernen von je sechs Reihen zu 16 Silben, jedesmal bis zum ersten fehlerfreien Hersagen. Die hierzu erforderliche Gesamtzeit betrug im Mittel 1261 Sekunden mit dem wahrscheinlichen Beobachtungsfehler ± 48,4; d. h. die Hälfte aller 84 Zahlen fällt in das Intervall 1213 bis 1309. Die Genauigkeit der Beobachtungen war also gegen früher erheblich gesteigert1): das von dem wahrscheinlichen Fehler eingeschlossene Intervall beträgt nur mehr 7 1/2 % des Mittelwertes, gegen 14 % bei den älteren Versuchen. Im einzelnen verteilen sich die Zahlen so:
| Es fallen innerhalb | d. h. innerhalb der Abweichung |
Anzahl der Abweichungen | |
| gezählt | berechnet | ||
| 1/10 w | ± 4 | 4 | 4,5 |
| 1/6 w | ± 8 | 7 | 7,6 |
| 1/4 w | ± 12 | 12 | 11,3 |
| 1/2 w | ± 24 | 23 | 22,2 |
| w | ± 48 | 44 | 42 |
| 11/2 w | ± 72 | 57 | 57,8 |
| 2 w | ± 96 | 68 | 69 |
| 21/2 w | ± 121 | 75 | 76 |
| 3 w | ± 145 | 81 | 80 |
1) Die hier erreichte Genauigkeit vermag natürlich keinen Vergleich mit physikalischen, wohl aber mit physiologischen Messungen auszuhalten, an die man naturgemäß auch zunächst denken wird. Zu den genauesten Messungen der Physiologie gehören die letzten Bestimmungen der Geschwindigkeit der Nervenleitung durch v. Helmholtz und Baxt. Eine als Beispiel für ihre Genauigkeit mitgeteilte Versuchsreihe dieser Untersuchungen (Mon. Ber. d. Berl. Akad. 1870, S. 191) gibt nach entsprechender Berechnung einen Mittelwert 4,268 mit dem wahrscheinlichen Beobachtungsfehler 0,101. Das von diesem eingeschlossene Intervall beträgt also 5 % des Mittelwertes. Alle früheren Bestimmungen sind bei weitem ungenauer. Bei der sichersten Versuchsreihe der ersten durch v. Helmholtz angestellten Messungen berechnet sich jenes Intervall auf ca. 50 % des Mittelwertes (Arch. f. Anat. u. Physiol. 1850, 8. 340). Auch die Physik muß sich übrigens, bei erstmaligen Untersuchungen, oft mit einer geringen Sicherheit ihrer Zahlen begnügen. Bei den ersten Bestimmungen des mechanischen Äquivalents der Wärme fand Joule die Zahl 838 m. d. wahrsch. Beobachtungsfehler 97. (Phil. Mag. 1843, S. 435 ff.)
Auch die Symmetrie der Verteilung ist hier, wenn man absieht von den Zahlen, die wegen ihrer Kleinheit nicht ins Gewicht fallen, befriedigend gewahrt.
| Es fallen innerhalb | Abweichungen | |
| nach unten | nach oben | |
| 1/6 w | 5 | 2 |
| 1/4 w | 7 | 5 |
| 1/2 w | 13 | 10 |
| w | 20 | 24 |
| 11/2 w | 28 | 29 |
| 2 w | 34 | 34 |
| 21/2 w | 37 | 38 |
| 3 w | 40 | 41 |
Die absolut größte Abweichung ist eine solche nach unten.
Wurden also mehrere unserer Silbenreihen zu Gruppen vereinigt und dann einzeln gelernt, so fielen zwar bei wiederholten Versuchen die Zeiten, welche für das Lernen einer ganzen Gruppe erforderlich waren, sehr verschieden von einander aus, aber trotzdem gruppierte sich ihre ganze Masse in eben derselben Weise wie die, untereinander ebenfalls differierenden, Werte, welche man bei Beobachtung begrifflich gleichartiger naturwissenschaftlicher Vorgänge erhält. Es darf also, mindestens versuchsweise, als erlaubt gelten, die aus mehreren jener Versuchszahlen gewonnenen Durchschnittswerte für die Feststellung ursächlicher Beziehungen ganz ebenso zu verwerten wie die Naturwissenschaft dies mit ihren Mittelwerten tut.
Die Anzahl von Silbenreihen, welche dabei zu einer Gruppe, zu einem Versuch, zusammenzufassen sind, ist natürlich durch nichts bestimmt. Man wird nur erwarten, dass mit wachsender Anzahl auch die Übereinstimmung zwischen der Gruppierung der gefundenen Zeiten und dem Fehlergesetz eine größere werde, und man wird praktisch diese Anzahl so groß zu nehmen suchen, dass eine noch weitere Steigerung derselben und die dadurch erzielte noch größere Übereinstimmung nicht mehr für den Mehraufwand von Zeit entschädigt, den sie erfordert. Verringert man die Zahl der Reihen jedes Versuchs, so wird voraussichtlich auch die gewünschte Übereinstimmung unvollkommener. Man wird indes verlangen, dass auch dann die Annäherung an die theoretisch geforderte Verteilung der Zahlen immer noch erkenntlich bleibe.
Auch dieser Forderung aber wird durch die gefundenen Zahlen Genüge geleistet. Bei den beiden eben beschriebenen größten Versuchsreihen habe ich die Zeiten untersucht, welche für das Lernen der ersten Hälfte jedes Versuchs erforderlich waren. Bei der älteren Reihe sind dies also die Lernzeiten für jedesmal 4, bei der jüngeren für jedesmal 3 Silbenreihen zusammengenommen. Es fand sich:
1. bei der älteren Reihe: Mittelwert (m) 533, wahrscheinlicher Beobachtungsfehler (wb) 51,
Verteilung der Einzelwerte
| Es fallen innerhalb |
d. h. innerhalb der Abweichung |
Anzahl der Abweichungen |
Von den Abweichungen fallen |
||
| gezählt | berechnet | nach unten | nach oben | ||
| 1/10 w | ± 5 | 2 | 5 | 2 | 0 |
| 1/6 w | ± 8 | 4 | 8,2 | 3 | 1 |
| 1/4 w | ± 12 | 6 | 12,3 | 4 | 2 |
| 1/2 w | ± 25 | 21 | 24,3 | 9 | 12 |
| w | ± 51 | 48 | 46 | 24 | 24 |
| 11/2 w | ± 76 | 61 | 63,4 | 30 | 31 |
| 2w | ± 102 | 76 | 75,6 | 37 | 39 |
| 21/2 w | ± 127 | 85 | 83,6 | 42 | 43 |
| 3 w | ± 153 | 89 | 88 | 45 | 44 |
2. bei der jüngeren Reihe: m = 620, wb = ± 44;
Verteilung der Einzelwerte
| Es fallen innerhalb |
d. h. innerhalb der Abweichung |
Anzahl der Abweichungen |
Von den Abweichungen fallen |
||
| gezählt | berechnet | nach unten | nach oben | ||
| 1/10 w | ± 4 | 3 | 4,5 | 1 | 2 |
| 1/6 w | ± 7 | 5 | 7,6 | 3 | 2 |
| 1/4 w | ± 11 | 11 | 11,3 | 6 | 5 |
| 1/2 w | ± 22 | 25 | 22,2 | 13 | 12 |
| w | ± 44 | 44 | 42 | 21 | 23 |
| 11/2 w | ± 66 | 56 | 57,8 | 29 | 27 |
| 2 w | ± 88 | 71 | 69 | 38 | 33 |
| 21/2 w | ± 110 | 76 | 76 | 41 | 35 |
| 3 w | ± 132 | 79 | 80 | 42 | 37 |
Durch beide Tabellen wird die eben gemachte Voraussetzung einer minder vollkommenen aber immer noch ersichtlichen Übereinstimmung zwischen der beobachteten und berechneten Gruppierung der Zahlen wohl bestätigt.
Ganz dieselbe annähernde Übereinstimmung nun wird auch vorausgesetzt werden müssen, wenn zwar nicht weniger Reihen zu einem Versuch zusammengenommen werden, wohl aber die Gesamtzahl der Versuche eine geringere ist. Auch hierfür füge ich noch einige bestätigende Übersichten bei.
Aus der Zeit der älteren Versuche besitze ich zwei größere Versuchsreihen, die im übrigen unter gleichen Umständen wie die oben erwähnte Reihe, aber zu den späteren Tageszeiten B und C gewonnen worden sind.
Die eine (B) umfaßt 39 Versuche mit je sechs, die andere (C) 38 Versuche mit je acht Einzelreihen, jede Einzelreihe zu 13 Silben. Es fand sich:
1. für die Versuche der Zeit B: m = 871, wb = ± 63.
Verteilung der Einzelwerte
| Es fallen innerhalb |
Anzahl der Abweichungen | |
| gezählt | berechnet | |
| 1/4 w | 4 | 5 |
| 1/2w | 10 | 10,3 |
| w | 21 | 19,5 |
| 11/2 w | 28 | 26,8 |
| 2 w | 32 | 32 |
| 21/2 w | 35 | 35,4 |
| 3 w | 37 | 37,3 |
2. für die Versuche der Zeit C: m = 1258, wb = ± 60.
Verteilung der Einzelwerte
| Es fallen innerhalb |
Anzahl der Abweichungen | |
| gezählt | berechnet | |
| 1/4 w | 7 | 5 |
| 1/2 w | 10 | 10 |
| w | 19 | 19 |
| 11/2 w | 26 | 26 |
| 2 w | 31 | 31 |
| 21/2 w | 34 | 34,5 |
| 3 w | 36 | 36,4 |
Außerdem erwähne ich noch eine Reihe von nur 20 Versuchen, mit der ich diese Übersichten abschließe. Jeder Versuch bestand in dem Lernen von acht dreizehnsilbigen Einzelreihen, welche gerade einen Monat vorher schon einmal gelernt worden waren. Das Mittel betrug in diesem Falle 892 Sekunden mit dem wahrscheinlichen Beobachtungsfehler 54. Die Einzelwerte gruppieren sich folgendermaßen:
| Es fallen innerhalb |
Anzahl der Abweichungen | |
| gezählt | berechnet | |
| 1/4 w | 3 | 2,7 |
| 1/2 w | 5 | 5,3 |
| w | 10 | 10 |
| 11/2w | 12 | 13,8 |
| 2 w | 17 | 16,5 |
| 21/2 w | 19 | 18,2 |
| 3 w | 20 | 19,1 |
Die Übereinstimmung zwischen der theoretischen Berechnung und der Zählung der Abweichungen ist in allen diesen Fällen noch eine so gute, dass man auch bei einer noch geringeren Anzahl von Versuchen den Mittelwerten – selbstverständlich immer nur mit Berücksichtigung der weiten Fehlergrenzen – eine Verwertbarkeit in dem oben mehrfach besprochenen Sinne zugestehen wird.
Die vorhin ausgesprochenen Vermutungen über die Gruppierung der für das Lernen der einzelnen Reihen erforderlichen Zeiten waren natürlich nicht bloß theoretische Voraussetzungen, sondern bereits bestätigt durch die Betrachtung tatsächlich gefundener Gruppierungen. Die beiden erwähnten größeren Versuchsreihen von 92 Versuchen zu acht und 84 Versuchen zu sechs Einzelreihen, also mit 736 und 504 Einzelwerten, geben dabei der Beurteilung eine genügend breite Unterlage. Beide Zahlengruppen zeigen nun und zwar beide in ganz analoger Weise, folgende Eigentümlichkeiten:
1. Die Streuung der Werte von ihrem arithmetischen Mittel nach oben ist merklich lockerer und reicht namentlich bedeutend weiter als nach unten. Die entferntesten Werte nach oben liegen 2-, resp. 1,8 mal soweit von dem Mittel wie die entferntesten nach unten.
2. Durch dieses Überwiegen hoher Zahlen wird das Mittel aus der Gegend der dichtesten Schaarung etwas nach oben abgelenkt, und dadurch wiederum bekommen die Abweichungen nach unten an Zahl das Übergewicht. Es entfallen 404 resp. 266 Abweichungen nach unten auf 329 resp. 230 nach oben.
3. Die Anzahl der Abweichungen von der Stelle größter Dichtigkeit aus nach beiden Seiten nimmt nicht gleichmäßig ab – wie man doch bei verhältnismäßig so hohen Gesamtzahlen sehr annähernd erwarten sollte –, sondern es zeigen sich deutlich noch mehrere Maxima und Minima der Anhäufung. Es waren demnach bei der Erzeugung der Einzelwerte, d. h. also bei dem Lernen der einzelnen Reihen, konstante Fehlerursachen im Spiel, welche teils eine unsymmetrische Streuung der Zahlen bewirkten, teils eine Anhäufung derselben in gewissen Gegenden begünstigten, und man kann nach den vorangegangenen Untersuchungen dieses Abschnitts nur voraussetzen, dass sich diese Einflüsse bei Zusammenfassung der Werte für mehrere hintereinander gelernte Reihen allmählich kompensierten.
Als wahrscheinliche Ursache der unsymmetrischen Verteilung machte ich schon die eigentümliche Verschiedenheit der Wirkung großer Aufmerksamkeits- und großer Zerstreuungsgrade geltend. Die Ursache der mehrfachen Anhäufung von Werten zu beiden Seiten des Mittels wird man unschwer in der Stellung der einzelnen Reihen innerhalb jedes Versuchs vermuten. Summiert man bei einer größeren Versuchsreihe die Werte für die sämtlichen ersten, die sämtlichen zweiten, dritten u. s. w. Reihen und nimmt aus diesen Summen jedesmal das Mittel, so fallen, wie man voraussieht, diese Mittel merklich verschieden aus. Die Einzelwerte jeder Summe gruppieren sich nun zwar nur mit mäßiger Annäherung nach dem Fehlergesetz um ihr Mittel, allein sie liegen doch ungefähr in seiner Gegend am dichtesten zusammen, und diese einzelnen Anhäufungen müssen sich nachher auch in der Gesamtmasse noch wieder zeigen.
Man wird ergänzend hinzufügen: wegen der, im Laufe eines Versuchs allmählich zunehmenden geistigen Ermüdung müßten jene Mittelwerte mit wachsender Ordnungszahl der Reihen immer größer werden; man trifft aber damit nicht den eigentümlichen Sachverhalt.
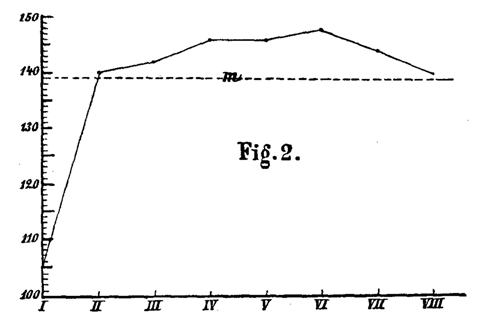
Nur in einem Falle nämlich habe ich etwas dieser Voraussetzung Entsprechendes konstatieren können, bei der großen und deshalb allerdings gewichtigen Versuchsreihe von 92 Versuchen mit acht dreizehnsilbigen Reihen. Bei dieser fanden sich für das Lernen der sämtlichen 92 ersten, zweiten u. s. w. Reihen die Mittelwerte 105, 140, 142, 146, 146, 148, 144, 140 Sekunden, deren relative Lage Fig. 2 veranschaulicht. Für alle übrigen Fälle, die ich untersuchte, ist dagegen vielmehr ein Gang der Zahlen typisch, wie er sich bei den 84 Versuchen mit sechs sechzehnsilbigen Reihen herausstellte und wie ihn Fig. 3 wiedergibt.
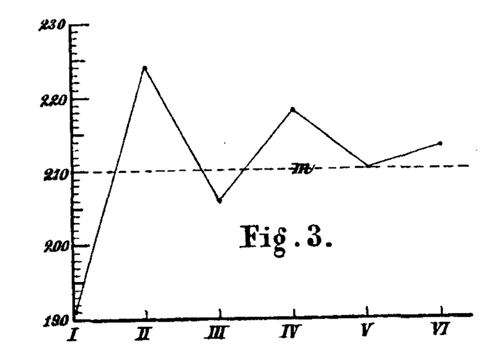
Die Mittel waren hier 191, 224, 206, 218, 210, 213 Sekunden. Dieselben setzen, wie man sieht, ziemlich tief unter dem Gesamtmittel ein, erheben sich aber sofort zu einer Höhe über demselben, die im weiteren Verlauf des Versuchs nicht wieder erreicht wird, und oszillieren dann in ziemlich beträchtlichen Schwankungen auf und nieder. Einen ganz analogen Gang zeigen z. B. die Zahlen bei 7 Versuchen mit je neun zwölfsilbigen Reihen, nämlich:
71, 90, 98, 87, 98, 90, 101, 86, 69 (Fig. 4),
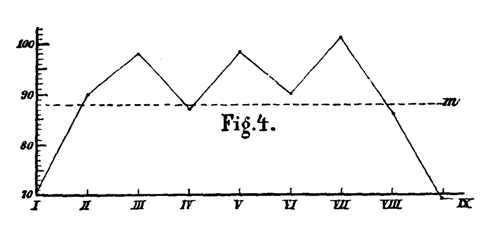
ferner die Werte für 39 Versuche mit sechs dreizehnsilbigen Reihen, die zur Zeit B gewonnen wurden
(118, 150, 158, 147, 155, 144 – Fig. 5 untere Kurve),
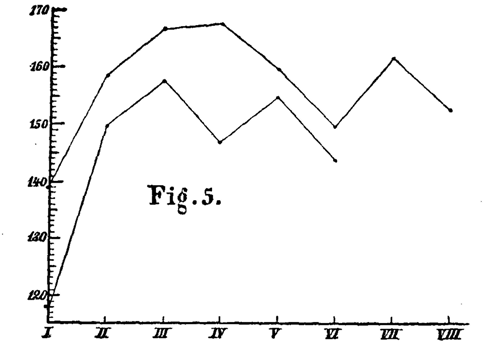
diejenigen für 38 Versuche mit acht 13silbigen Reihen der Zeit C (139, 159,167, 168, 160, 150, 162, 153 – Fig. 5 oben), sowie endlich die aus 7 Versuchen mit je sechs Stanzen des Byronsehen Don Juan erhaltenen Zahlen (189, 219, 171, 204, 183, 229) u. s. w.
Ja, auch bei der ersterwähnten widersprechenden Gruppe von Versuchen zeigt sich eine übereinstimmende Gruppierung der Einzelmittel mit der sonst allgemein gefundenen, wenn man die je 92 Reihen nicht alle zugleich in Rechnung zieht, sondern in einige Fraktionen teilt, d. h. also, wenn man Versuche zusammenfaßt, die sich zeitlich näher stehen und bei denen eine größere Ähnlichkeit der Versuchsumstände vorausgesetzt werden kann.
Man darf natürlich aus diesen Zahlen nicht schließen, dass ein Einfluß der allmählich zunehmenden geistigen Abspannung während der – je etwa 20 Minuten dauernden – Versuche nicht stattgefunden habe.
Man muß nur sagen, dass der vorauszusetzende Einfluß der letzteren auf die Zahlen bei weitem übertroffen wird durch eine andere Tendenz, auf die man a priori nicht so leicht gekommen wäre, nämlich durch eine Tendenz, auf verhältnismäßig niedrige Werte verhältnismäßig hohe folgen zu zulassen und umgekehrt. Es scheint eine Art periodischer Oszillation der geistigen Empfänglichkeit oder der Aufmerksamkeit zu bestehen, bei der dann die zunehmende Ermüdung sich so äußern würde, dass die Schwankungen um eine allmählich sich verschiebende Mittellage geschehen2).
2) Wenn es einmal von Interesse werden sollte, könnte man auch noch versuchen, die verschiedenen Effekte jener Tendenz in verschiedenen Fällen numerisch näher zu präzisieren. Ein Maß nämlich für den Einfluß der zahlreichen zufälligen Störungen, denen das Auswendiglernen von einem Tag zum anderen ausgesetzt ist, hat man in den wahrscheinlichen Beobachtungsfehlern der für Reihengruppen erhaltenen Zahlen. Wäre nun das Lernen der einzelnen Reihen im allgemeinen nur denselben oder ähnlichen Schwankungen der Umstände ausgesetzt, wie sie von Versuch zu Versuch stattfinden, so müßte, nach den Grundsätzen der Fehlertheorie, ein aus den Einzelwerten direkt berechneter wahrscheinlicher Beobachtungsfehler sich zu dem eben erwähnten verhalten wie l : 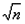 , wo n die Anzahl der zu einem Versuch zusammengenommenen Einzelreihen bezeichnet. Machen sich aber bei dem Lernen dieser Einzelreihen, wie es in unserem Falle scheint, noch besondere Einflüsse geltend, welche die Werte stärker von einander treiben als es die sonstigen Schwankungen der Umstände tun würden, so muß das aus den Einzelwerten berechnete wb etwas zu groß ausfallen, das eben genannte Verhältnis also zu klein, und zwar beides um so mehr, je stärker solche Tendenzen wirken.
, wo n die Anzahl der zu einem Versuch zusammengenommenen Einzelreihen bezeichnet. Machen sich aber bei dem Lernen dieser Einzelreihen, wie es in unserem Falle scheint, noch besondere Einflüsse geltend, welche die Werte stärker von einander treiben als es die sonstigen Schwankungen der Umstände tun würden, so muß das aus den Einzelwerten berechnete wb etwas zu groß ausfallen, das eben genannte Verhältnis also zu klein, und zwar beides um so mehr, je stärker solche Tendenzen wirken.
Eine Prüfung des tatsächlichen Verhaltens ist zwar etwas mühsam, bestätigt das Gesagte aber vollkommen. Bei den 84 Versuchen mit sechs sechzehnsilbigen Reihen ist = 2,45. Als wahrscheinlichen Beobachtungsfehler der 84 Versuchszahlen fanden wir 48,4. Der wahrscheinliche Beobachtungsfehler der 504 Einzelwerte ist 31,6. Der Quotient 31,6 : 48,4 ist 1,53; also nicht einmal ⅔ des Wertes von 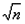 .
.
Nach diesen Orientierungen über die Art und die Verwendbarkeit der durch das Auswendiglernen gewonnenen Zahlen, wenden wir uns nunmehr zu dem eigentlichen Zweck der Untersuchung, der numerischen Beschreibung von Kausalverhältnissen.